一种基于Bezier-凸优化的运载火箭上升段轨迹规划方法与流程

一种基于bezier
‑
凸优化的运载火箭上升段轨迹规划方法
技术领域
1.本发明属于火箭制导技术领域，具体涉及一种运载火箭上升段轨迹规划方法。


背景技术：

2.随着航天科技的快速发展，运载火箭在不同发射任务下对自主性和智能化要求越来越高。由于运载火箭上升段具有复杂的动力学约束和过程约束，上升段轨迹优化问题很难在机载计算机上实时求解。因此，能够处理复杂约束的可靠、快速的方法成为近些年来计算制导领域研究的重点与难点。一般而言，运载火箭上升段轨迹规划问题可以表述为一个具有目标函数、状态和控制约束的最优控制问题，传统上有两种方法来解决这个问题：间接法和直接法。其中间接法是利用变分法和庞特里亚金极大(极小)值原理，推导最优控制问题的一阶必要条件，从而转化为两点边值问题或多点边值问题进行求解。间接法的优点是求解精度高，求解速度快，但同时也存在收敛半径小，迭代算法对初始猜想极其敏感，复杂模型的一阶必要条件推导繁琐等问题。直接法将最优控制问题通过离散方法转化为非线性规划问题进行求解，其优点是不需要推导一阶必要条件，易于处理复杂约束问题，具有良好的通用性。但该方法一般需要大规模的数值优化求解，计算比较缓慢，此外也存在所求得的仅仅是近似解及存在维数灾难等不足。
3.凸优化作为一种特殊的直接法，因其对理论解和计算效率的保证得到了广泛的应用。但由于大部分航空航天问题都存在强非线性的动力学模型和状态约束，无法直接采用凸优化进行求解。因而近年来，逐次线性化法和newton
–
kantorovich(n
‑
k)法被提出对这类问题进行凸化，他们都是将原问题转化为一系列子凸优化问题，然后采用内点法求解子问题，将该次迭代求得的子问题的解作为下一次迭代的初值。不同的是，逐次线性化法是利用泰勒展开将非线性微分方程转化为关于状态量和控制量的线性微分方程，收敛性无法保证，且对初始猜测比较敏感；而n
‑
k法是利用变分法和广义泰勒展开将非线性微分方程转化为关于状态增量和控制增量的线性微分方程，具有稳定收敛的形式，且对初值不敏感。因此n
‑
k法作为非线性动力学方程的凸化方法可以更快收敛到最优解，为轨迹规划问题的在线求解提供了技术保证。


技术实现要素：

4.为了克服现有技术的不足，本发明提供了一种基于bezier
‑
凸优化的运载火箭上升段轨迹规划方法，针对传统方法收敛性差，计算效率低，无法应用于在线轨迹规划等缺陷，提出了一种基于bezier曲线的改进凸优化方法。首先，建立运载火箭上升段轨迹规划的最优控制问题；其次，利用n
‑
k方法处理高度非线性的动力学微分方程，将其转化为关于状态增量和控制增量的线性微分方程，且具有稳定收敛的形式，提升了方法的收敛速度；最后，利用bezier曲线代替控制量曲线，有效地降低了凸优化问题的求解规模，极大地提升了凸优化问题的求解效率。本发明能有效解决含有复杂约束的运载火箭上升段在线轨迹规划问题。
5.本发明解决其技术问题所采用的技术方案包括如下步骤：
6.步骤1：在发射惯性坐标系下，建立运载火箭上升段动力学模型如下：
[0007][0008]
式中，自变量为运载火箭的高度h，x和y为运载火箭在地面的投影位置，v为运载火箭的速度，γ为运载火箭航迹倾角，χ为运载火箭航向角，m为运载火箭的质量，α为攻角，σ为倾侧角，t为推力，i
sp
为发动机比冲，g0为地球引力常数，g＝mg为重力，l＝ρv2s
ref
c
l
/2为升力，d＝ρv2s
ref
c
d
/2为阻力，其中ρ为大气密度，s
ref
为运载火箭的参考面积，c
l
和c
d
分别为升力系数和阻力系数；
[0009]
式(1)简写为其中x＝[x,y,v,γ,χ,m]
t
为状态量，u＝[u1,u2,u3,t]
t
为控制量，u1＝cosα，u2＝sinαcosσ，u3＝sinαsinσ；
[0010]
步骤2：建立运载火箭上升段轨迹规划的最优控制问题p0，性能指标为终端速度最大，约束方程包括：运载火箭上升段动力学方程、初始和终端状态约束方程、过程约束方程、控制量约束方程；
[0011]
最优控制问题p0表示为：
[0012]
min j＝
‑
v(h
f
)
[0013]
s.t.
[0014]
x(h0)＝x0[0015]
α
min
≤α≤α
max
,σ
min
≤σ≤σ
max
,t
min
≤t≤t
max
[0016][0017]
x(h
f
)＝x
f
,y(h
f
)＝y
f
,γ(h
f
)＝γ
f
,χ(h
f
)＝χ
f
,m(h
f
)≥m
dry
ꢀꢀꢀ
(2)
[0018]
其中，x0＝[x0,y0,v0,γ0,χ0,m0]
t
为运载火箭期望的初始状态量；攻角α约束的上下限为
±
90
°
，α
min
＝
‑
90
°
，α
max
＝90
°
，该约束能表示为控制量u1的约束：u1≥0；倾侧角σ约束的上下限为
±
90
°
，σ
min
＝
‑
90
°
，σ
max
＝90
°
，该约束能表示为控制量u2和u3的约束：
‑
1≤u2≤1，
‑
1≤u3≤1；此外，三个控制量还满足约束u
12
u
22
u
32
＝1；t
min
和t
max
为推力的最小值和最大值；过程约束包括动压约束q≤q
max
，轴向推力加速度约束a
axial
≤a
max
和弯矩约束q
α
≤q
αmax
，q
max
为动压允许的最大值，a
max
为轴向推力加速度允许的最大值，q
αmax
为弯矩允许的最大值；x
f
，y
f
，γ
f
，χ
f
为运载火箭期望的终端状态量，m
dry
为运载火箭的结构质量；h0和h
f
表示初始高度和终端高度；
[0019]
步骤3：用bezier曲线代替最优控制问题p0的控制量u的曲线，运载火箭上升段轨迹规划问题的控制变量变为bezier曲线的控制点：控制量约束方程变为关于bezier曲线控制点的约束方程，从而得到基于bezier的最优控制问题p1；
[0020]
步骤3
‑
1：所述bezier曲线的表达式为：
[0021][0022]
其中，p
i
为bezier曲线的控制点，为伯恩斯坦多项式；t为归一化的自变量，n为控制点个数；
[0023]
将运载火箭上升段动力学模型的自变量归一化处理，令ω＝(h
‑
h0)/(h
f
‑
h0)，ω为动力学模型归一化后的自变量，此时新的性能指标变为j＝
‑
v(1)，新的动力学模型变为x
′
＝dx/dω＝(h
f
‑
h0)f(x，u)；
[0024]
步骤3
‑
2：用bezier曲线的控制点代替控制量u＝[u1，u2，u3，t]
t
：
[0025][0026]
其中，p
kj
是bezier曲线的控制点；为伯恩斯坦多项式；
[0027]
将式(4)表示成矩阵的形式：
[0028]
u
s
(ω)：＝w(ω)p
s
；p
s
＝[p
s0
，...，p
sn
]
t
[0029][0030]
步骤3
‑
3：bezier曲线控制点的约束方程为：
[0031]
轴向推力加速度约束，
[0032]
弯矩约束，
[0033]
推力约束，
[0034]
控制量约束，
[0035]
控制量约束，
[0036]
步骤3
‑
4：基于bezier的最优控制问题p1表示为：
[0037]
min j＝
‑
v(1)
[0038]
s.t.x
′
＝(h
f
‑
h0)f(x，p)
[0039]
x(0)＝x0，x(1)＝x
f
，y(1)＝y
f
，γ(1)＝γ
f
，χ(1)＝χ
f
，m(1)≥m
dry
[0040][0041][0042]
步骤4：利用n
‑
k方法对运载火箭上升段动力学方程和过程约束进行凸化，得到关于状态增量δx和控制增量δp的线性微分方程和凸的过程约束，利用松弛技巧对控制量约束进行凸化，得到凸的控制量约束，从而得到基于bezier曲线的子凸优化问题p2：
[0043]
步骤4
‑
1：利用n
‑
k方法对运载火箭上升段动力学方程和过程约束进行凸化：
[0044]
定义非线性算子f[x，p]＝x
′‑
f(x，p)＝0，对非线性算子进行广义泰勒展开并忽略高阶项：
[0045]
f[x δx，p δp]＝f[x，p] f
x
(x，p)[δx] f
p
(x，p)[δp]＝0
ꢀꢀꢀꢀ
(8)
[0046]
其中，δx和δp分别为状态量和控制量的增量，f
x
(x，p)[δx]和f
p
(x，p)[δp]为frechet导数；
[0047][0048][0049]
步骤4
‑
2：将式(9)和式(10)带入广义泰勒展开式(8)，得到关于状态增量δx和控制增量δu
*
的线性微分方程：
[0050][0051]
步骤4
‑
3：基于bezier曲线的子凸优化问题p2表示为：
[0052]
min j＝
‑
δv(1)
[0053]
s.t.
[0054]
δx(0)＝x0‑
x(0)
[0055]
δx(1)＝x
f
‑
x(1)，δy(1)＝y
f
‑
y(1)，δγ(1)＝γ
f
‑
γ(1)，δχ(1)＝χ
f
‑
χ(1)，δm(1)≥m
dry
‑
m(1)
[0056][0057]
t
min
≤p
4j
δp
4j
≤t
max
，0≤p
1j
δp
1j
≤1，
‑
1≤p
2j
δp
2j
≤1，
‑
1≤p
3j
δp
3j
≤1(p
1j
δp
1j
)2 (p
2j
δp
2j
)2 (p
3j
δp
3j
)2≤1
ꢀꢀꢀ
(12)
[0058]
步骤5：对子凸优化问题p2进行离散化，将自变量进行等距离散得到ω0，ω1，...，ω
n
，优化变量表示为向量动力学方程采用欧拉法进行离散，得到基于bezier曲线的离散子凸优化问题p3表示为：
[0059]
min j＝c
t
z
[0060]
s.t.
[0061]
δx1＝x0‑
x1[0062]
δx
n
＝x
f
‑
x
n
，δy
n
＝y
f
‑
y
n
，δγ
n
＝γ
f
‑
γ
n
，δχ
n
＝χ
f
‑
χ
n
，δm
n
≥m
dry
‑
m
n
[0063][0064]
t
min
≤p
4j
δp
4j
≤t
max
，0≤p
1j
δp
1j
≤1，
‑
1≤p
2j
δp
2j
≤1，
‑
1≤p
3j
δp
3j
≤1
[0065]
(p
1j
δp
1j
)2 (p
2j
δp
2j
)2 (p
3j
δp
3j
)2≤1
[0066]
其中，i＝1，2，...，n，j＝0，1，...，n，且n＞＞n；n为变量离散点的个数；
[0067]
步骤6：采用内点法求解基于bezier曲线的离散子凸优化问题p3，将该次迭代求得的子问题的解作为下一次迭代的初值，直到迭代收敛至最优解，具体求解过程为：
[0068]
步骤6
‑
1：令迭代步数k＝0，给定状态量和控制量的初始猜想x0和p0，并令初始猜想x
k
＝x0，p
k
＝p0；
[0069]
步骤6
‑
2：在第k 1步迭代过程中，将所述初始猜想x
k
和p
k
结合凸优化求解器
‑‑
mosek求解器，求解所述基于bezier曲线的离散子凸优化问题p3，得到状态量增量δx和控制量增量δp；
[0070]
步骤6
‑
3：更新状态量和控制量：x
k 1
＝x
k
δx，p
k 1
＝p
k
δp；
[0071]
步骤6
‑
4：判断是否满足收敛条件：max(δx
i
)≤ε，若满足该条件，则停止迭代，x
k 1
和p
k 1
为优化问题的解；若不满足则令x
k
＝x
k 1
，p
k
＝p
k 1
；返回步骤6
‑
2。
[0072]
本发明的有益效果如下：
[0073]
本发明将传统凸优化方法与bezier曲线和n
‑
k方法相结合，利用n
‑
k方法处理具有强非线性的运载火箭上升段动力学方程，具有良好的收敛性；利用少量的bezier曲线的控制点代替数量较多的离散控制量，降低了问题的求解维度，此外由于bezier曲线的凸包性，也减少了一些过程约束和控制量约束的数量，有效地提高了问题的求解效率，实现了运载火箭在强非线性动力学和复杂过程约束情况下的在线轨迹规划。
附图说明
[0074]
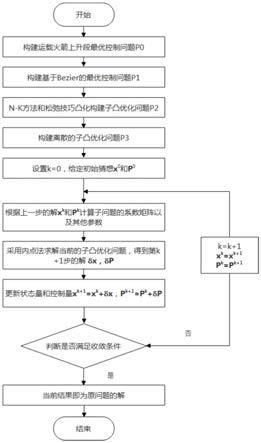
图1为本发明方法的结构框图。
[0075]
图2为本发明方法与参考方法空间三维轨迹曲线。
[0076]
图3为本发明方法与参考方法速度随高度的变化曲线。
[0077]
图4为本发明方法与参考方法航迹倾角随高度的变化曲线。
[0078]
图5为本发明方法与参考方法攻角和倾侧角随高度的变化曲线。
[0079]
图6为本发明方法与参考方法动压，轴向推力加速度和弯矩随高度的变化曲线。
[0080]
图7为本发明方法与参考方法在不同离散点数量情况下总计算时间的对比曲线。
[0081]
图8为本发明方法与参考方法在不同离散点数量情况下终端速度的对比曲线。
[0082]
图9为本发明方法与参考方法在不同离散点数量情况下积分与优化结果的终端位置误差曲线。
[0083]
图10为本发明方法与参考方法在不同离散点数量情况下积分与优化结果的终端速度误差曲线。
具体实施方式
[0084]
下面结合附图和实施例对本发明进一步说明。
[0085]
本发明解决的技术问题是：针对现有技术不足，提供一种基于改进凸优化的运载火箭上升段轨迹规划方法，克服传统凸优化方法在求解复杂航天问题时收敛性差和求解效率低的问题，实现含有复杂约束和强非线性动力学方程的运载火箭上升段的轨迹在线规划。
[0086]
步骤1：在发射惯性坐标系下，建立运载火箭上升段动力学模型如下：
[0087][0088]
式中，自变量为运载火箭的高度h，x和y为运载火箭在地面的投影位置，v为运载火箭的速度，γ为运载火箭航迹倾角，χ为运载火箭航向角，m为运载火箭的质量，α为攻角，σ为倾侧角，t为推力，i
sp
为发动机比冲，g0为地球引力常数，g＝mg为重力，上＝ρv2s
ref
c
l
/2为升力，d＝ρv2s
ref
c
d
/2为阻力，其中ρ为大气密度，s
ref
为运载火箭的参考面积，c
l
和c
d
分别为升力系数和阻力系数；
[0089]
式(1)简写为其中x＝[x，y，v，γ，χ，m]
t
为状态量，u＝[u1，u2，u3，t]
t
为控制量，u1＝cosα，u2＝sinαcosσ，u3＝sinαsinσ；
[0090]
步骤2：建立运载火箭上升段轨迹规划的最优控制问题p0，性能指标为终端速度最大，约束方程包括：运载火箭上升段动力学方程、初始和终端状态约束方程、过程约束方程、控制量约束方程；
[0091]
最优控制问题p0表示为：
[0092]
min j＝
‑
v(h
f
)
[0093]
s.t.
[0094]
x(h0)＝x0[0095]
α
min
≤α≤α
max
，σ
min
≤σ≤σ
max
，t
min
≤t≤t
max
[0096][0097]
x(h
f
)＝x
f
，y(h
f
)＝y
f
，γ(h
f
)＝γ
f
，χ(h
f
)＝χ
f
，m(h
f
)≥m
dry
ꢀꢀꢀ
(2)
[0098]
其中，x0＝[x0，y0，v0，γ0，χ0，m0]
t
为运载火箭期望的初始状态量；攻角α约束的上下限为
±
90
°
，α
min
＝
‑
90
°
，α
max
＝90
°
，该约束能表示为控制量u1的约束：u1≥0；倾侧角σ约束的上下限为
±
90
°
，σ
min
＝
‑
90
°
，σ
max
＝90
°
，该约束能表示为控制量u2和u3的约束：
‑
1≤u2≤1，
‑
1≤u3≤1；此外，三个控制量还满足约束t
min
和t
max
为推力的最小值和最大值；过程约束包括动压约束q≤q
max
，轴向推力加速度约束a
axial
≤a
max
和弯矩约束q
α
≤q
αmax
，q
max
为动压允许的最大值，a
max
为轴向推力加速度允许的最大值，q
αmax
为弯矩允许的最大值；x
f
，y
f
，γ
f
，χ
f
为运载火箭期望的终端状态量，m
dry
为运载火箭的结构质量；
[0099]
步骤3：用bezier曲线代替最优控制问题p0的控制量u的曲线，运载火箭上升段轨迹规划问题的控制变量变为bezier曲线的控制点：控制量约束方程
变为关于bezier曲线控制点的约束方程，从而得到基于bezier的最优控制问题p1；
[0100]
步骤3
‑
1：所述bezier曲线的表达式为：
[0101][0102]
其中，p
i
为bezier曲线的控制点，为伯恩斯坦多项式
[0103]
由于bezier曲线的自变量在0到1的范围，为了用bezier曲线代替控制量曲线，首先需要将运载火箭上升段动力学模型的自变量归一化处理，令ω＝(h
‑
h0)/(h
f
‑
h
0)，ω为动力学模型归一化后的自变量，此时新的性能指标变为j＝
‑
v(1)，新的动力学模型变为x
′
＝dx/dω＝(h
f
‑
h0)f(x，u)；
[0104]
步骤3
‑
2：用bezier曲线的控制点代替控制量u＝[u1，u2，u3，t]
t
：
[0105][0106]
其中，p
kj
是bezier曲线的控制点；为伯恩斯坦多项式；
[0107]
将式(4)表示成矩阵的形式：
[0108]
u
k
(ω)：＝w(ω)p
k
；p
k
＝[p
k0
，...，p
kn
]
t
；k＝1，2，3，4
[0109][0110]
步骤3
‑
3：bezier曲线控制点的约束方程为：
[0111]
轴向推力加速度约束，
[0112]
弯矩约束，
[0113]
推力约束，
[0114]
控制量约束，
[0115]
控制量约束，
[0116]
由于bezier曲线的凸包性，即bezier曲线总是位于由其控制点组成的凸包内，因此只要bezier控制点满足的约束，bezier曲线上任意一点都满足该约束，从而可以极大减少一些过程约束和控制量约束的数量，从而缩小问题的求解规模；
[0117]
步骤3
‑
4：基于bezier的最优控制问题p1表示为：
[0118]
min j＝
‑
v(1)
[0119]
s.t.x
′
＝(h
f
‑
h0)f(x，p)
[0120]
x(0)＝x0，x(1)＝x
f
，y(1)＝y
f
，γ(1)＝γ
f
，χ(1)＝χ
f
，m(1)≥m
dry
[0121][0122][0123]
步骤4：利用n
‑
k方法对运载火箭上升段动力学方程和过程约束进行凸化，得到关于状态增量δx和控制增量δp的线性微分方程和凸的过程约束，利用松弛技巧对控制量约束
进行凸化，得到凸的控制量约束，从而得到基于bezier曲线的子凸优化问题p2；
[0124]
步骤4
‑
1：利用n
‑
k方法对运载火箭上升段动力学方程和过程约束进行凸化：
[0125]
定义非线性算子f[x，p]＝x
′‑
f(x，p)＝0，对非线性算子进行广义泰勒展开并忽略高阶项：
[0126]
f[x δx，p δp]＝f[x，p] f
x
(x，p)[δx] f
p
(x，p)[δp]＝0
ꢀꢀꢀ
(8)
[0127]
其中，δx和δp分别为状态量和控制量的增量，f
x
(x，p)[δx]和f
p
(x，p)[δp]为frechet导数；
[0128][0129][0130]
步骤4
‑
2：将式(9)和式(10)带入广义泰勒展开式(8)，得到关于状态增量δx和控制增量δu
*
的线性微分方程：
[0131][0132]
值得注意的是，上述线性微分方程左端项为非线性算子f[x，p]的导数，右端项为负的非线性算子，因此上式可以写为f
′
＝
‑
f的形式，这是一种稳定控制的形式，f[x，p]的所有参数都可以指数收敛到收敛解，因此n
‑
k方法对初始猜测不敏感且具有更快的收敛速度。
[0133]
步骤4
‑
3：基于bezier曲线的子凸优化问题p2表示为：
[0134]
min j＝
‑
δv(1)
[0135]
s.t.
[0136]
δx(0)＝x0‑
x(0)
[0137]
δx(1)＝x
f
‑
x(1)，δy(1)＝y
f
‑
y(1)，δγ(1)＝γ
f
‑
γ(1)，δχ(1)＝χ
f
‑
χ(1)，δm(1)≥m
dry
‑
m(1)
[0138][0139]
t
min
≤p
4j
δp
4j
≤t
max
，0≤p
1j
δp
1j
≤1，
‑
1≤p
2j
δp
2j
≤1，
‑
1≤p
3j
δp
3j
≤1
[0140]
(p
1j
δp
1j
)2 (p
2j
δp
2j
)2 (p
3j
δp
3j
)2≤1
ꢀꢀꢀ
(12)
[0141]
这里应用松弛技巧将非凸的控制量约束(p
1j
δp
1j
)2 (p
2j
δp
2j
)2 (p
3j
δp
3j
)2＝1转化为凸的控制量约束(p
1j
δp
1j
)2 (p
2j
δp
2j
)2 (p
3j
δp
3j
)2≤1，这样处理得到的解被证明与原问题的解是相同的；
[0142]
步骤5：对子凸优化问题p2进行离散化，将自变量进行等距离散得到ω0，ω1，...，ω
n
，优化变量表示为向量动力学方程采用欧拉法进行离散，得到基于bezier曲线的离散子凸优化问题p3表示为：
[0143]
min j＝c
t
z
[0144]
s.t.
[0145]
δx1＝x0‑
x1[0146]
δx
n
＝x
f
‑
x
n
，δy
n
＝y
f
‑
y
n
，δγ
n
＝γ
f
‑
γ
n
，δχ
n
＝χ
f
‑
χ
n
，δm
n
≥m
dry
‑
m
n
[0147][0148]
t
min
≤p
4j
δp
4j
≤t
max
，0≤p
1j
δp
1j
≤1，
‑
1≤p
2j
δp
2j
≤1，
‑
1≤p
3j
δp
3j
≤1
[0149]
(p
1j
δp
1j
)2 (p
2j
δp
2j
)2 (p
3j
δp
3j
)2≤1
[0150]
其中，i＝1，2，...，n，j＝0，1，...，n，且n＞＞n；
[0151]
步骤6：采用内点法求解基于bezier曲线的离散子凸优化问题p3，将该次迭代求得的子问题的解作为下一次迭代的初值，直到迭代收敛至最优解，具体求解过程为：
[0152]
步骤6
‑
1：令迭代步数k＝0，给定状态量和控制量的初始猜想x0和p0，并令初始猜想x
k
＝x0，p
k
＝p0；
[0153]
步骤6
‑
2：在第k 1步迭代过程中，将所述初始猜想x
k
和p
k
结合凸优化求解器
‑‑
mosek求解器，求解所述基于bezier曲线的离散子凸优化问题p3，得到状态量增量δx和控制量增量δp；
[0154]
步骤6
‑
3：更新状态量和控制量：x
k 1
＝x
k
δx，p
k 1
＝p
k
δp；
[0155]
步骤6
‑
4：判断是否满足收敛条件：max(δx
i
)≤ε，若满足该条件，则停止迭代，x
k 1
和p
k 1
为优化问题的解；若不满足则令x
k
＝x
k 1
，p
k
＝p
k 1
；返回步骤6
‑
2。
[0156]
具体实施例：
[0157]
本实施例以多级运载火箭的子一级为仿真对象，推力t＝2961.6
×
103n，比冲i
sp
＝2556.2n
·
s/kg，参考面积s
ref
＝4m2，结构质量m
dry
＝70696kg，最大动压q
max
＝3
×
104n/m2，最大轴向推力加速度a
max
＝5gm/s2，最大弯矩q
αmax
＝3
×
103n
·
rad/m2；自变量飞行高度设置为h∈[5，63]km，仿真初始条件设置为：初始位置x0＝0km，y0＝0km，初始速度v0＝225.5m/s，初始航迹倾角γ0＝80.8deg，初始航向角χ0＝0deg，初始质量m0＝2.124
×
105kg；终端条件设置为：终端位置x
f
＝40.5km，y
f
＝0km，终端航迹倾角γ
f
＝44.5deg，终端航向角χ
f
＝0deg；计算机硬件条件为inter core i5
‑
4210m cpu2.60ghz，软件使用基于matlab的mosek求解器。
[0158]
如图1所示，本发明提供的基于bezier
‑
凸优化的运载火箭上升段轨迹规划方法包括以下步骤：
[0159]
1、确定无量纲化参数，令长度的无量纲化参数为地心矢径r0，速度的无量纲化参数为时间的无量纲化参数为质量的无量纲化参数为初始质量m0，且r0＝6378.13km，g0＝9.807m/s2；确定离散点个数n＝200和bezier控制点个数n＝20；
[0160]
2、对运载火箭上升段参考轨迹进行初始化，首先根据上述参数确定运载火箭初始的运动状态x0＝[0，0，0.0285，1.4104，0，0.7478]
t
，给定控制量的初始猜想其中p
10
设为元素都为1的20
×
1的向量，p
20
和p
30
设为大小为20
×
1的零向量，设为元素都为最大推力的20
×
1的向量，并通过龙格库塔积分计算出一条参考轨迹；然后将飞行高度h0＝7.8393
×
10
‑4到h
f
＝0.0099的变化范围均匀离散为200个区间，得到h＝[h1，h2，...，h
n
]，并将初始参考轨迹插值到每一个对应的离散高度上，得到一条离散
的初始参考轨迹令迭代步数k＝0，初始猜想x
k
＝x0，p
k
＝p0；
[0161]
3、在第k 1步迭代过程中，将所述初始猜想x
k
和p
k
结合凸优化求解器mosek求解器，求解所述基于bezier曲线的离散子凸优化问题p3，具体步骤为：
[0162]
(3a)性能指标的离散形式写成矩阵相乘的形式j＝c
t
z，其中向量c＝[01×
1202
，
‑
1，01×
83
]
t
，优化变量
[0163]
(3b)根据x
k
和p
k
计算每个离散点的f
i
，构成离散的动力学约束方程并将其写成矩阵形式mz＝f，其中
[0164][0165][0166]
[0167][0168][0169]
(3c)分别获得所述运载火箭上升段的初始状态凸化方程，终端状态凸化方程，过程凸约束以及控制量凸约束方程，构建离散的运载火箭上升段bezier
‑
凸优化子问题：
[0170]
min j＝c
t
z
[0171]
s.t.mz＝f
[0172]
δx1＝x0‑
x1[0173]
δx
n
＝x
f
‑
x
n
，δy
n
＝y
f
‑
y
n
，δγ
n
＝γ
f
‑
γ
n
，δχ
n
＝χ
f
‑
χ
n
，δm
n
≥m
dry
‑
m
n
[0174][0175]
t
min
≤p
4j
δp
4j
≤t
max
，0≤p
1j
δp
1j
≤1，
‑
1≤p
2j
δp
2j
≤1，
‑
1≤p
3j
δp
3j
≤1
[0176]
(p
1j
δp
1j
)2 (p
2j
δp
2j
)2 (p
3j
δp
3j
)2≤1
[0177]
(3d)结合mosek求解器的语法规则，对离散化的bezier
‑
凸优化子问题进行求解，得到状态量增量δx和控制量增量δp；
[0178]
4、更新状态量和控制量：x
k 1
＝x
k
δx，p
k 1
＝p
k
δp；
[0179]
5、设定本方法法的收敛条件为并判断是否满足收敛条件：max(δx
i
)≤ε，若满足该条件，则停止迭代，x
k 1
和p
k 1
为原优化问题的解；若不满足则令x
k
＝x
k 1
，p
k
＝p
k 1
返回第3步。
[0180]
根据上述步骤，本发明所提出的基于bezier
‑
凸优化的运载火箭上升段轨迹规划
方法规划出一条满足各项约束的最优轨迹计算经历了2次迭代，总耗时为0.1180s，以目前最新的改进凸优化方法n
‑
k伪谱凸优化(n
‑
k/pcp)为参考，该方法在相同的参数设置和硬件条件下的计算经历了4次迭代，总耗时为4.8103s，由此证明了本发明所提方法具有收敛速度快，求解效率高的有益效果。
[0181]
图2给出了基于bezier
‑
凸优化的运载火箭上升段轨迹规划方法规划出的最优三维轨迹曲线，可以清楚地看到，本发明方法与参考方法的优化结果一致且满足终端位置约束；图3和图4给出了本发明方法规划的最优速度曲线和航迹倾角曲线，可以看出本发明方法与参考方法优化结果基本相同；图5给出了本发明方法规划的攻角和倾侧角变化曲线，可以看到本发明方法相比于参考方法优化的控制量更加平滑，这得益于bezier曲线光滑的特性；图6给出了本发明方法的动压，轴向推力加速度和弯矩变化曲线，可以看到三者都严格满足了过程约束。
[0182]
为了进一步说明本发明方法的快速性和精确性，在不同离散点数量下对比了本发明方法与参考方法n
‑
k/pcp方法的求解时间，性能指标和终端误差；图7给出了两种方法的计算时间随离散点数量的变化曲线，可以看出本发明方法求解时间远小于参考方法，且随着离散点数量增多，这种优势越明显；图8给出了两种方法优化的最大终端速度对比曲线，可以看出本发明方法优化的性能指标略小于参考方法，但由于计算时间的大幅降低，这种结果也是可以接受的；图9和图10给出了两种方法的终端位置误差和终端速度误差，此处的终端误差为最优控制量的龙格库塔积分解与优化解之间的误差，可以看出本发明方法的终端误差均保持在允许的误差范围内且远小于参考方法的终端误差。
[0183]
本发明提供的一种基于bezier
‑
凸优化的运载火箭上升段轨迹规划方法，与现有技术相比，通过将传统凸优化与n
‑
k方法和bezier曲线相结合，利用n
‑
k方法处理高度非线性的动力学微分方程，将其转化为关于状态增量和控制增量的线性微分方程，且具有稳定收敛的形式，提升了方法的收敛速度；利用bezier曲线代替控制量曲线，由于bezier曲线可以由少数控制点决定，因此优化控制量减少为少量的bezier控制点，减少了优化变量的数量，同时由于bezier曲线的凸包性，部分过程约束和控制量约束也减少为关于控制点的约束，有效地降低了凸优化问题的求解规模，极大地提升了每步迭代凸优化子问题的求解效率，该方法具有在线求解复杂约束的轨迹规划问题的潜力。