具有丢包和多时滞的网络控制系统的最优控制研究方法与流程

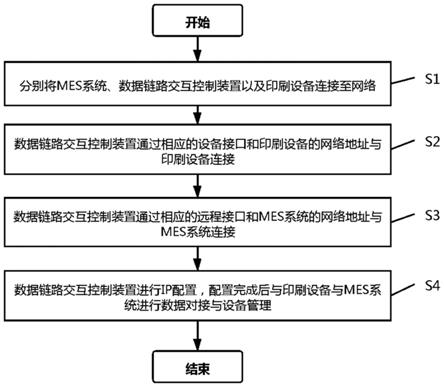
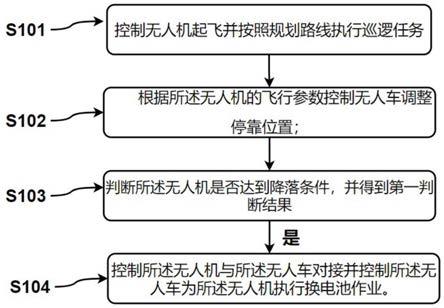
技术特征：
1.具有丢包和多时滞的网络控制系统的最优控制研究方法，其特征在于：首先给出如下定义：符号表示n维欧氏空间；上标'表示矩阵的转置；实数矩阵m＞0表示矩阵m是正定的；实数矩阵m≥0表示矩阵m是半正定的；表示指示函数，即当元素时，有否则有则有是由随机过程x所产生的自然滤波；e[
·
]是数学期望且是关于的条件期望；p(x)表示当事件x发生时的概率；i表示单位矩阵；δ
kl
表示克罗内克函数，即当k＝l时有δ
kl
＝1，否则有δ
kl
＝0；所述方法具体包括如下步骤：步骤1：利用带有时滞的量测数据{y
k
}设计出了最优估计器；步骤2：利用极大值原理，解出了最优控制器，并给出了有限时间范围内可解的充分必要条件；且最优控制器的增益为耦合的黎卡提方程的解；步骤3：通过定义一个李雅普诺夫函数，得出系统在均方意义下是可镇定的，当且仅当给定的耦合的黎卡提方程有唯一解。2.根据权利要求1所述的具有丢包和多时滞的网络控制系统的最优控制研究方法，其特征在于：在步骤2中，具体设计如下：有限时间的情况问题描述考虑下面带有丢包、输入时滞和量测时滞的乘性噪声系统：y
k
＝ω
k
x
k
‑
θ
，
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)；其中，代表状态向量，代表控制器，代表其协方差为的标量高斯白噪声；代表量测过程，ω
k
是服从概率为p(ω
k
＝1)＝p＝1
‑
q∈[0,1]的伯努利分布；a,b,是具有适当维数的常值矩阵，d和θ(>0)分别表示输入时滞和量测时滞；初始值x0表示均值为μ，协方差为θ的高斯随机向量，初始控制器u
i
,i＝
‑
d,...,θ
‑
1的值是已知的，而且{ω
k
}和x0彼此相互独立；系统(1)和(2)的性能指标定义为：其中，常值矩阵分别是用来平衡状态向量和输入向量的权重矩阵，x
n 1
为终端状态向量，为有界的常数终端加权矩阵；对于具有丢包和多时滞的乘性噪声系统，控制器u
k
只允许访问量测过程{y
θ
,...,y
k
}，也就是说，u
k
是可量测的；为了方便起见，将表示为同时，将表示为将表示为问题1对于系统(1)和(2)，利用量测数据{y
k
}，找到一个可量测的控制器u
k
使得目标函数(3)最小；为了确保问题的可解性，给出下面的假设：假设1目标函数(3)中矩阵满足q≥0，r>0和m
n 1
≥0；
最优估计在求解最优控制器之前，首先给出最优估计器的表达式；为了表示方便，将估计器表示为下面给出本小节的重要定理：定理1对于系统的状态方程(1)和量测方程(2)，最优估计器的递推式为：其中初始值为且有和p(ψ
k
＝1)＝q＝1
‑
p，θ≤k≤n，表示指示函数；除此之外，由系统方程(1)能够直接计算得到证首先计算最优估计器的初始值令y
θ
＝ω
θ
x0＝h，则由条件期望的定义得到其中，p(x
θ
＝r
i
|y
θ
＝h)表示在y
θ
＝h发生的情况下x
θ
取值为r
i
的条件概率；下面进行讨论：1)对于量测数据y
θ
，当出现数据丢包时，也就是说y
θ
＝h＝0，此时有p(x
θ
＝r
i
,y
θ
＝0)＝p(x
θ
＝r
i
)p(y
θ
＝0)，则由(5)得到2)当没有发生丢包时，也即y
θ
＝h≠0，则由(5)得到因此，结合式(6)和(7)，估计器的初始值表示为由于系统噪声和{ω
k
}是相互独立的，则通过系统状态方程(1)得到下面进一步分析最优估计器的一般形式θ≤k≤n；为了方便起见，令y
k
＝{y
θ
,...,y
k
}；类比式(5)，利用条件期望的定义，可得分类讨论如下：1)若y
θ
＝y
θ 1
...＝y
k
＝0，则有p(x
k
＝r
i
,y
θ
＝0,y
θ 1
＝0,...,y
k
＝0)＝p(x
k
＝r
i
)p(yθ＝0,y
θ 1
＝0,...,y
k
＝0)；因此，根据式(8)得e[x
k
|y
θ
＝h
θ
,y
θ 1
＝h
θ 1
,...,y
k
＝h
k
]＝ex
k
ꢀꢀꢀ
(9)；
2)若有y
k
＝h
k
＝0,且其中{θ,θ 1,...,k
‑
1}＝{i
θ
,i
θ 1
,...,i
k
‑1}，i
θ
＜i
θ 1
＜...＜i
j
；此时有；此时有则根据式(8)得3)若k时刻没有数据丢包，即y
k
＝h
k
≠0，估计器能够表示为其中y
k
＝ω
k
x
k
‑
θ
，且上式第二行利用了状态{x
k
}的马尔可夫特性；由式(1)和(11)得同理可得则由式(12)和(13)，式(11)中的估计器能够写成递推的形式，如下：综上所述，由式(9)
‑
(11)得最优估计器的形式为同时由系统方程(1)直接计算得下面对式(14)作进一步的化简；利用指示函数的特性知下面对式(14)作进一步的化简；利用指示函数的特性知因此，当y
θ
＝y
θ 1
...＝y
k
＝0时，由式(16)，式(14)能够写为e[x
k
|y
θ
,...,y
k
]＝ex
k
＝ae[x
k
‑1|y
k
‑1] bu
k
‑
d
‑1ꢀꢀꢀꢀꢀꢀꢀꢀ
(18)；同时，若有其中i
θ
＜i
θ 1
＜...＜i
j
＜...≤i
k
‑1，则1)当i
j
＜k
‑
1时，即且y
k
‑1＝0，由式(17)，式(14)能够写为2)当i
j
＝k
‑
1时，即y
k
‑1≠0，由式(17)，式(14)能够写为
因此，由式(14)，(18)
‑
(20)，并将定义为ψ
k
，得到最优估计器的递推形式为上式即为式(4)；最优输出反馈控制为了得到问题1的解，对系统状态方程(1)和目标函数(3)应用极大值原理得到如下的共态方程：λ
n
＝m
n 1
x
n 1
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(21)；(21)；其中下面给出问题1完整的解；定理2基于假设1，对于系统(1)和(2)，问题1有唯一的解，当且仅当矩阵δ
k
＞0，k＝d θ,...,n；且设计的令目标函数(3)最小的最优输出反馈控制器为其中估计器满足下式估计器已经在定理1中给出，且增益δ
k d
和γ
k d
满足满足在式(25)和(26)中，矩阵ψ
k
,φ
k
满足下列的黎卡提差分方程满足下列的黎卡提差分方程满足下列的黎卡提差分方程满足下列的黎卡提差分方程φ
k
＝(1
‑
q)a
′
ψ
k 1
a a
′
φ
k 1
a，
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(31)；式(27)
‑
(31)中的终端条件为ψ
n 1
＝0,φ
n 1
＝0；同时可得式(3)中的最优目标函数为
且状态和共态之间的关系满足下式推论令对式(27)
‑
(31)两端从i＝3到d 1进行累加，得到下面耦合的黎卡提方程(31)两端从i＝3到d 1进行累加，得到下面耦合的黎卡提方程(31)两端从i＝3到d 1进行累加，得到下面耦合的黎卡提方程φ
k
＝(1
‑
q)a
′
ψ
k 1
a a
′
φ
k 1
a，
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(37)；上式中的终端值为ξ
n 1
＝π
n 1
＝m
n 1
，且矩阵δ
k
和γ
k
能够直接计算得到能够直接计算得到下面给出定理2的证明：证首先给出必要性的证明，即在假设1的前提下，如果问题1有唯一解，式(25)中的矩阵δ
k
，d θ≤k≤n是严格正定的；定义新的目标函数为令式(40)中的k＝n，得到j(n)＝e[x
n
′
qx
n
u
n
‑
d
′
ru
n
‑
d
] x
n 1
′
m
n 1
x
n 1
；将系统的状态方程(1)代入上式，则j(n)能够写成状态x
n
和控制器u
n
‑
d
的二次型形式，且由于控制器解的唯一性，该二次型必然是正定的；令状态x
n
＝0，得到因此δ
n
＞0成立；下面计算最优控制器；由式(1)和(21)，平衡方程(23)能够写为因此，当k＝n时的最优控制器为明显式(41)满足式(24)；接下来说明k＝n时的共态方程具有式(33)的形式；利用式(1)、(21)、(22)和(41)，得到上式满足式(33)，且矩阵m
n1
和分别满足式(27)和(28)；为了进一步分析一般情况，并利用数学归纳法，取d θ≤l≤n，当k≥l 1，假设式(25)中的矩阵是正定的，且控制器u
k
‑
d
和共态λ
k
‑1的表达式为式(24)和(33)；接下来证明该情形在k
＝l时也成立；首先需要证明矩阵δ
l
的可逆性；由式(1)、(22)和(23)，得到将上式从k＝l 1到n进行累加，得到利用上式以及式(21)，并令式(40)中的k＝l，则j(l)表示成将式(33)代入上式，并令x
l
＝0，则j(l)被写成由于最优控制器解u
l
‑
d
的唯一性，则式(25)中矩阵δ
l
是严格正定的，也即δ
l
＞0成立；下面求解最优控制器；将式(33)代入式(23)得到则最优控制器的解为其中矩阵δ
l
和γ
l
分别满足式(25)和(26)；因此，最优控制器(24)在k＝l时也成立；最后证明状态和共态之间的关系式满足式(33)，如下：显然该式成立；这就完成了必要性的证明；
下面给出充分性的证明，即当式(25)中的矩阵δ
k
＞0，k＝d θ,...,n时，证明问题1有唯一解；定义则由式(1)、(25)
‑
(31)，能够计算得到v
n
(k 1,x
k 1
)如下)如下令v
n
(k,x
k
)和v
n
(k 1,x
k 1
)作差，得到对式(41)两端从k＝d θ到n进行累加，得到利用上式将目标函数写为
在上式中，x0,u
i
,i＝
‑
d,...,θ
‑
1已经初始化，对于0≤k≤d θ
‑
1，x
k
能够由初始值进行求解，且矩阵δ
k
是严格正定的；因此，令目标函数取到最小值，最优控制器的唯一性即得证，且满足式(24)。3.根据权利要求1所述的具有丢包和多时滞的网络控制系统的最优控制研究方法，其特征在于：在步骤3中，具体设计如下：无限时间的情况问题描述为了分析系统的镇定性，求解系统(1)和(2)在无限时间时的镇定问题；当n
→
∞时考虑如下的性能指标：首先给出下面几个重要的定义：定义1对于给定的初始值x0,u
‑
d
,...,u
θ
‑1，且控制器u
k
‑
d
＝0,k≥d θ，如果有则称方程(1)为渐进均方稳定的；定义2方程(1)在均方意义下是可镇定的，当存在一个可量测的控制器其中l和l
i
(i＝1,...,d θ)是常值矩阵，且满足使得(1)的闭环系统是渐进均方稳定的；定义3对于下面的随机系统为了方便起见，将上述系统简记为基于假设1，有q＝c'c成立；如果有下式成立则称系统是完全可观测的；问题2找到一个可测的控制器u
k
‑
d
使得系统(1)是渐进均方稳定的，同时使得目标函数(44)最小；假设2是完全可观测的；问题2的解为了表述清晰，将矩阵δ
k
,γ
k
,ψ
k
,φ
k
,ξ
k
,π
k
写为δ
k
(n),γ
k
(n),ψ
k
(n),
φ
k
(n),ξ
k
(n),π
k
(n)；由于终端值m
n 1
＝0，故上述矩阵都为时不变矩阵；下面给出几个重要引理：引理1基于假设1，得到π
k
(n)≥ξ
k
(n)≥0,ψ
k
(n)＜0，φ
k
(n)＜0和证在定理1中已经证得了δ
k
(n)＞0，k≥d θ，由式(28)
‑
(31)能够直接观察得出矩阵ψ
k
(n),φ
k
(n)都是负定的；接下来证明π
k
(n)≥ξ
k
(n)≥0和成立；定义其中m≥d θ；由式(3)和(32)能够类比得到式(45)的最优解为其中m≥d θ；由式(3)和(32)能够类比得到式(45)的最优解为对式(46)分析如下：其中有同理得同理得则由式(46)
‑
(49)；得到由于状态x
d θ
是随机变量，因此，得到ξ
d θ
(m)≥0；也即由定理2看出则必有利用ξ
d θ
(m),和的时不变特性，令m＝n d θ
‑
k，则有ξ
k
(n)＝ξ
d θ
(n d θ
‑
k)≥0,和因此不等式π
k
(n)≥ξ
k
(n)≥0，和也成立；引理2基于假设1和2，存在一个常数n0>0，使得当n＞n0时，有ξ
d θ
(n)＞0；
证对于式(46)，选定状态向量x
d θ
(≠0)，则有假设ξ
d θ
(n)＝0成立，那么式(46)能够写为其中和分别代表最优状态策略和最优控制器；由假设1可知，q＝c'c≥0且r＞0，再由式(51)能够观察得出则系统方程(1)能够写成基于定义3和假设2，得到x
d θ
＝0，矛盾；因此假设不成立，则有n0>0，使得当n＞n0时，有ξ
d θ
(n)＞0成立；引理3系统方程(1)是可镇定的，当且仅当不等式成立；证首先给出充分性的证明；显然，如果成立，则必有基于定义2可知系统方程(1)是可镇定的；下面证明必要性，即若系统方程(1)是镇定的，则不等式成立；由定义2可知，存在使得系统方程(1)是渐进均方稳定的；定义如下矩阵如下矩阵
利用上述矩阵可将系统方程(1)转变为一个新的状态方程为且控制器u
k
能够写为将式(53)代入式(52)得到回顾定义2知，控制器使系统方程(1)渐进均方稳定，也即存在同时，我们能够得到则由式(54)能够直接得到且有因此得利用式(55)，能够得到也即定理3系统方程在均方意义下是镇定的，当且仅当推论中耦合的黎卡提方程有唯一解，且有π≥ξ＞0,m1≥0,ψ,φ≤0和m
j
≤0,j＝2,...,d 1：≤0,j＝2,...,d 1：ψ＝
‑
(a
′
)
d
γ
′
δ
‑1γa
d
qa
′
ψa
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(58)；φ＝(1
‑
q)a
′
ψa a
′
φa
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(59)；其中δ和γ为其中δ和γ为使系统镇定的控制器为式(44)对应的最优目标函数为
其中下面给出定理3的证明：必要性：即若系统方程(1)是均方能够镇定的，则式(34)
‑
(39)中耦合的黎卡提方程有唯一解，且π≥ξ＞0,ψ,φ≤0；首先给出矩阵ξ
d θ
(n),π
d θ
(n),ψ
d θ
(n)和φ
d θ
(n)关于n的单调性证明；回顾式(32)和(42)，最优目标函数能够写为其中，且u
j
＝0,j＝
‑
d,...,
‑
1,1,下面对式(65)进行讨论：1)如果有x0＝ex0成立，则由定理1可以得到那么式(65)能够写为由于j
*
(n)≤j
*
(n 1)能够得到也即π0(n)≤π0(n 1)成立；2)如果有ex0＝0成立，能够得到类比上述分析得3)对于给定的x
d θ
，由式(46)，令m＝n，可有h
*
(n)≤h
*
(n 1)，则得也即ξ
d θ
(n)≤ξ
d θ
(n 1)成立；
综上所述，看出π0(n),和ξ
d θ
(n)关于n是单调递增的；下面证明上述矩阵是有界的；由定义2知，存在控制器使得系统方程(1)镇定；选定一常数λ使得q≤λi,成立；则有其中c和c1是常数；因此，得到再由式(50)，知上式表明矩阵ξ
d θ
(n)是有界的；类比式(65)进行如下讨论：1)若x0＝ex0，则有故有上式表明矩阵是有界的；2)若ex0＝0，则有故有得出也是有界的；综上知矩阵ξ
d θ
(n),π0(n),ψ0(n)和φ0(n)都是收敛的；且上述矩阵都是时不变矩阵，即有ξ
d θ
(n)＝ξ0(n
‑
d
‑
θ),π
d θ
(n)＝π0(n
‑
d
‑
θ)；φ
d θ
(n)＝φ0(n
‑
d
‑
θ)；因此，存在矩阵ξ,π,m1,ψ和φ，满足,ψ和φ，满足,ψ和φ，满足同时，在式(25)，(26)，(28)和(29)两端取极限得到收敛值为
因此，当时间变量n
→
∞，式(56)
‑
(61)是成立的；且利用引理1和2直接得到，π≥ξ＞0,m1≥0,ψ＜0,φ＜0和m
j
≤0,j＝2,...,d 1；最后证明式(56)
‑
(59)的解是唯一的；现假设存在另外一组解h,f,p和k也满足式(56)
‑
(59)；当有x0＝ex0时，对式(66)两端取极限，得到j
*
(n)＝e(x
′0πx0)＝e(x
′0fx0)；则有π＝f；而且若有ex0＝0，得j
*
(n)＝e{x
′0[π0(n)
‑
qψ0(n)
‑
qφ0(n)]x0}＝e{x
′0[f0(n)
‑
qp0(n)
‑
qk0(n)]x0}；由式(30)和(31)，看出φ
k
(n)依赖于ψ
k
(n)，也即若ψ0(n)≠p0(n)，则有φ0(n)≠k0(n)，这与上述方程式矛盾；故在该方程两侧取极限得到ψ＝p，φ＝k；同时，对于给定的x
d θ
，在式(51)两端取极限，直接得到e(x
′
d θ
ξx
d θ
)＝e(x
′
d θ
hx
d θ
)，则有ξ＝h；综上知式(56)
‑
(61)的解是唯一的；充分性：若式(56)
‑
(61)中耦合的黎卡提方程有唯一解，则控制器(62)能够使得系统方程(1)镇定；首先，令同时经计算也能够得到则对k≥d θ，有从式(69)看出，控制器满足式(62)，且函数v(k,x
k
)关于n是单调递减的；同时经计算得到上式表明函数v(k,x
k
)是有界的，由单调有界原理知函数v(k,x
k
)是收敛的；因此，通过式(69)得到
再由式(50)得在式(71)两端取极限并利用式(70)，得利用引理2知ξ
d θ
(n)＞0，则有也即式(62)中的控制器能够使得系统方程(1)镇定；接下来证明控制器(62)能够使目标函数(44)最小为(63)；对式(68)两端从k＝0到n进行累加，得到其中v(0,x0)和v(n 1,x
n 1
)已在式(67)中给出定义；利用射影定理有我们已经得到控制器(62)能够使得系统(1)镇定，因此有则在式(72)两端对n取极限，目标函数(44)能够写为通过以上的分析，控制器(62)能够使得目标函数(44)最小，且最优目标函数为式(63)。

技术总结
本发明公开了一种具有丢包和多时滞的网络控制系统的最优控制研究方法，属于网络控制领域。本文分析了带有乘性噪声、丢包、输入和量测时滞的离散网络控制系统中的最优输出反馈控制和镇定性问题。对于带有丢包和量测时滞的乘性噪声系统，首次给出了递归的最优估计器。基于该估计器，利用极大值原理求得了最优输出反馈控制器。同时给出了有限时间范围内最优控制问题可解的充分必要条件。最后，基于标准的可观性假设，证明了在均方意义下设计的控制器可以使得系统方程镇定，当且仅当耦合的黎卡提方程有唯一解。方程有唯一解。方程有唯一解。


技术研发人员：梁笑 吕传志 刘瑞国 高学辉 张桂林
受保护的技术使用者：山东科技大学
技术研发日：2021.07.15
技术公布日：2021/11/4