一种用于考虑生物活性对耳蜗感音放大机制贡献的计算方法与流程

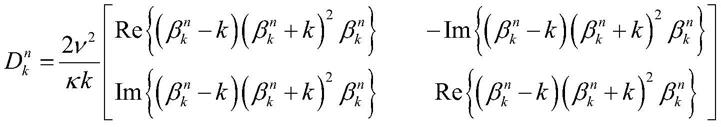
1.本发明属于生物物理技术领域，具体涉及一种用于考虑生物活性对耳蜗感音放大机制贡献的计算方法。


背景技术：

2.耳聋是一种最常见的人类感觉系统障碍性疾病，全球有3.6亿人(全世界人口的5％)患耳聋疾病。感音神经性耳聋是最具挑战性的医学难题，耳蜗主动感音放大机理作为耳医学的重大难题。基底膜是耳蜗感音功能中的关键宏观结构，诺贝尔获奖者冯贝克西提出了基底膜行波振动模型，以往报道的耳蜗计算分析模型都是基于行波理论，迄今为止，对于耳蜗主动放大机制的认识，均局限于耳蜗内各组织结构的相互作用和能量转换使得基底膜及微观组织的运动产生放大效应，然而并未考虑其本身作为生物活性结构的材料随时间变化的效应。即未考虑基底膜的生物活性。


技术实现要素：

3.本发明的目的是通过提出一种用于考虑生物活性对耳蜗感音放大机制贡献的计算方法及电池成组架构，以解决上述背景技术中提出的缺陷。
4.基于物理力学理论建立无因次化的耳蜗内淋巴液与基底膜耦合运动的控制方程，并将基底膜的运动行为通过体积力项引入navier-stokes方程中与流体运动进行耦合。
5.全面考虑基底膜的刚度随空间和时间同时变化的周期性函数以描述基底膜的生物活性,研究基底膜在不受到外界激励下，通过本身内部材料的周期性变化与淋巴液耦合振动行为。
6.本发明采用的技术方案如下：
7.一方面提供一种用于考虑生物活性对耳蜗感音放大机制贡献的计算方法，包括。
8.进行解析模型建立，并进行系统稳定性分析，再进行非周期性求解和周期性求解，得出系统共振特性。
9.作为本发明的一种优选技术方案：所述解析模型建立包括体积力f的计算：
[0010][0011]
式中，δ(x)表示二维的dirac delta函数，x(s,t)表示基底膜在拉格朗日坐标系下的位置参数，x0(s)＝(s,0)表示处在平衡位置；
[0012]
基底膜的刚度参数假定随着时间和空间进行变化，因此可通过函数表示为：
[0013]
k(s,t)＝σe-λs
(1 2τsin(ωt))
[0014]
式中，σ是平均时程弹性刚度常数，λ描述了沿基底膜空间的刚度变化，从以往试验数据整理发现基底膜的刚度沿长度呈现指数的变化规律，因此采用指数函数描述刚度的空间变化，另外，通过幅值参数τ和频率ω来描述基底膜周期性振动过程中的刚度的周期性变化规律；
[0015]
根据流体与基底膜的耦合振动界面条件，推得：
[0016][0017]
采用无因次化处理，无因次量如下：
[0018][0019]
式中，有波浪线上标的为无因次量，uc和pc分别表示速度和压强的特征尺度件，将无因次量代入得：
[0020][0021][0022][0023][0024][0025]
速度和压强的特征尺度表示为：
[0026][0027]
方程中的参数可表示为：
[0028][0029]
系统方程为：
[0030][0031]
▽
·
u＝0
[0032]
并且有以下条件：
[0033]
p＝-κe-αx
(1 2τsint)h(x,t)
[0034]
u(x,0,t)＝0
[0035][0036]
其中，h(x,t)表示基底膜的竖向位移，p(x,t)＝p(x,0

,t)-p(x,0-1
,t)表示基底膜上的压强差，u(x,y,t)和v(x,y,t)分别是纵向和竖向的速度。
[0037]
作为本发明的一种优选技术方案：所述系统的解满足以下形式：
[0038]
u(x,t)＝e
γt
p(x,t)
[0039]
式中，函数p(x,t)表示周期为2π的周期性函数，指数项系数决定了当t-》∞时，解的稳定性在[-π,π]区间内将p(x,t)进行级数化表示，可得：
[0040][0041][0042][0043][0044]
式中，p(x,t)进行了空间和时间的傅里叶级数展开。上述方程中需要进行求解的参数是沿y轴变化的傅里叶系数u
kn
,v
kn
,p
kn
；代入可得到关于压强方程为：
[0045][0046]
式中，由于线性无关特性，因此有：
[0047][0048]
求解上式，可得：
[0049][0050][0051]
进一步推导可到常微分方程为：
[0052][0053]
式中，
[0054]
假定γ in≠0,且k≠0，则上式的解为：
[0055][0056]
根据连续性得方程：
[0057][0058]
解之有：
[0059][0060]
根据连续性，可推得界面边界条件：
[0061][0062][0063]
进一步推导可得：
[0064][0065][0066]
带入可得：
[0067][0068]
当γ in＝0且k＝0时，则上式可简化为：
[0069][0070]
将上式中的指数函数和正弦函数进行傅里叶展开，有1 2τsint＝1-iτe
it
iτe-it
[0071]
对指数函数进行偶函数周期展开，并且当γ in≠0且k≠0时，有：
[0072][0073]
对于γ in＝0且k＝0时，有：
[0074][0075]
其中，
[0076]
是指数函数的傅里叶系数；针对ε
kn
项的系数进行整理，可得：
[0077][0078]
对于γ in＝0且k＝0时，有：
[0079][0080]
为了确保解的偶函数空间对称性，有：
[0081][0082][0083]
针对解u(x,t)＝e
γt
p(x,t)，有如下周期性条件：
[0084]
u(x,t 2πn)＝e
γ(t 2πn)
p(x,t)＝ξnu(x,t)
[0085]
如果γ＝0，则ξ＝1,并且有：
[0086]
u(x,t 2π)＝u(x,t)
[0087]
上式为以2π为周期的谐波解。如果γ＝1/2*i，则ξ＝-1,并且有：
[0088]
u(x,t 2π)＝-u(x,t),u(x,t 4π)＝u(x,t)
[0089]
对系统方程进行缩减，另n＝0,1,...,n,且k＝1,2,...,m，通过矩阵表示，可得：
[0090][0091]
其中，
[0092]
上述方程总共有2*m*(n 1)个待求解未知系数，a和b为斜对角矩阵；斜对角矩阵a可表示为a＝diag(a0，a1，...，an)，并且有以下形式：
[0093][0094]
其中，
[0095][0096][0097]
三角形斜对角矩阵b有如下形式：
[0098]
[0099]
其中，
[0100][0101]
a和b矩阵都已知，即：
[0102][0103]
其中，上述方程中的稳定性解的特征值为1/τ。
[0104]
作为本发明的一种优选技术方案：所述非周期性求解包括：
[0105]
当基底膜的刚度函数中τ＝0时，刚度函数为非周期性函数，方程的解是稳定的，且解的傅里叶系数满足：
[0106][0107]
当k＝0有：
[0108][0109]
上式中，φ＝ν2/κ＝π3μ2/(ρσl3)，它表示流体粘性阻力相对于基底膜弹性力的比值；上述方程可表示为其中t矩阵依赖于参数φ、γ和α。系统存在非奇异解的条件是满足det(t)＝0，当给定φ和α时，通过求解可得到γ。
[0110]
作为本发明的一种优选技术方案：所述周期性求解包括通过求解式
[0111][0112]
和
[0113][0114]
可得到τ以及对应的特征矢量，在此基础上，通过式
[0115][0116]
求解出周期性的解h(x,t)。
[0117]
本发明该结构紧凑、操作简单，通过将短梁绕光轴垂直旋转90
°
，可使安装于固定座之上的桌板竖直放置，避免了桌板的拆装收纳，有利于节省房车内部空间，具有较强实用性和应用价值。
附图说明
[0118]
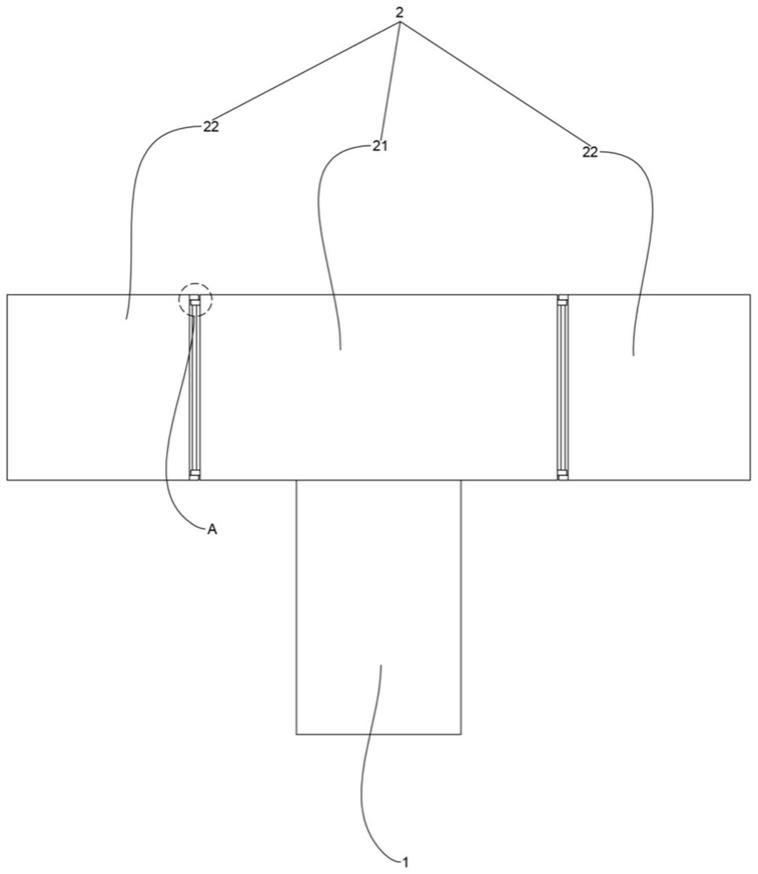
图1为本发明优选实施例的二维耳蜗模型图；
[0119]
图2为本发明优选实施例中满足det(t)＝0的γ的实部和虚部解图；
[0120]
图3为本发明优选实施例中无因次化的基底膜位移幅值曲线图；
[0121]
图4为本发明优选实施例中基底膜振动的峰值位置随频率的变化关系图；
[0122]
图5为本发明优选实施例中基底膜位移随时间变化曲线图；
[0123]
图6为本发明优选实施例中基底膜位移随时间变化曲线图(其中ω＝400s-1
,τ＝0.05,0.08和0.1分别对应上、中、下)；
[0124]
图7为本发明优选实施例中基底膜位移随时间变化曲线图(其中ω＝600s-1
,τ＝0.05,0.08和0.1分别对应上、中、下)；
[0125]
图8为本发明优选实施例中基底膜位移随时间变化曲线图(其中ω＝800s-1
,τ＝0.05,0.08和0.1分别对应上、中、下)；
[0126]
图9为本发明优选实施例中不同频率下基底膜的位移随位置的变化曲线图。
具体实施方式
[0127]
需要说明的是，在不冲突的情况下，本实施例中的实施例及实施例中的特征可以相互组合，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0128]
参照图1-9，本发明优选实施例提供了一种用于考虑生物活性对耳蜗感音放大机制贡献的计算方法。
[0129]
本发明主要分析耳蜗系统中的感音结构基底膜的振动特性，因此对耳蜗模型进行了合理简化，考虑简化的2维耳蜗模型，如图1所示。耳蜗通道为两腔体矩形结构，长为l，半腔体高度为h，基底膜位于腔体的中心。研究基底膜的本质特征对振动产生的影响。图1中实线表示基底膜离开平衡位置的振动，虚线代表基底膜的平衡位置，定义沿耳蜗长度方向为x轴，沿厚度方向为y轴。
[0130]
基于不可压缩的n-s方程，有：
[0131][0132]
▽
·
u＝0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
[0133]
式中，u(x,t)为流体速度，p(x,t)为压强，ρ为密度，μ表示粘度系数。本发明主要研究刚度在时空的变化，则体积力f为：
[0134][0135]
式中，δ(x)表示二维的dirac delta函数，x(s,t)表示基底膜在拉格朗日坐标系下的位置参数，x0(s)＝(s,0)表示处在平衡位置。方程的体积力f由基底膜的内在性质刚度k(s,t)来决定，通过基底膜刚度的参数的变化，可以描述基底膜内在性质调整下的振动特性。基底膜的刚度参数假定随着时间和空间进行变化，因此可通过函数表示为：
[0136]
k(s,t)＝σe-λs
(1 2τsin(ωt))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0137]
式中，σ是平均时程弹性刚度常数，λ描述了沿基底膜空间的刚度变化，从以往试验
数据整理发现基底膜的刚度沿长度呈现指数的变化规律，因此采用指数函数描述刚度的空间变化。另外，通过幅值参数τ和频率ω来描述基底膜周期性振动过程中的刚度的周期性变化规律。
[0138]
根据流体与基底膜的耦合振动界面条件，可推得：
[0139][0140]
为了使本发明具有共性，采用无因次化处理，无因次量如下：
[0141][0142]
式中，有波浪线上标的为无因次量。uc和pc分别表示速度和压强的特征尺度。将上述无因次量代入式(4)中可得：
[0143][0144][0145][0146][0147][0148]
速度和压强的特征尺度表示为：
[0149][0150]
因此，方程(6)和(9)中的参数可表示为：
[0151][0152]
针对以上建立的方程，为了进行求解和分析，还需要进一步处理。由于基底膜振幅一般在纳米尺度，这相比耳蜗通道的尺寸而言非常小，这意味流体的雷诺数很小，因此流体的非线性效应可以忽略。另外，基底膜的振动主要以横向y方向振动为主，本模型只考虑y方向的振动。综上，系统方程可为：
[0153][0154]
▽
·
u＝0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(14)
[0155]
并且有以下条件：
[0156]
p＝-κe-αx
(1 2τsint)h(x,t)
[0157]
u(x,0,t)＝0
[0158]
[0159]
其中，h(x,t)表示基底膜的竖向位移，p(x,t)＝p(x,0

,t)-p(x,0-1
,t)表示基底膜上的压强差，u(x,y,t)和v(x,y,t)分别是纵向和竖向的速度。
[0160]
由于系统中存在随时间变化的刚度参数，采用系统的解满足以下形式：
[0161]
u(x,t)＝e
γt
p(x,t)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(16)
[0162]
式中，函数p(x,t)表示周期为2π的周期性函数，指数项系数决定了当t-》∞时，解的稳定性。在[-π,π]区间内将p(x,t)进行级数化表示，可得：
[0163][0164][0165][0166][0167]
式中，p(x,t)进行了空间和时间的傅里叶级数展开。上述方程中需要进行求解的参数是沿y轴变化的傅里叶系数u
kn
,v
kn
,p
kn
。将式(17
‑‑
19)代入式(13)和(14)中可得到关于压强的泊松方程，表示为：
[0168][0169]
式中，由于线性无关特性，因此有：
[0170][0171]
通过求解式(22)，可得：
[0172][0173]
将式(18)代入式(13)中，有：
[0174][0175]
进一步推导可到常微分方程为：
[0176][0177]
式中，
[0178]
假定γ in≠0,且k≠0，则式(25)的解为：
[0179][0180]
根据连续性得方程：
[0181][0182]
解之有：
[0183][0184]
根据连续性，可推得界面边界条件：
[0185][0186][0187]
进一步推导可得：
[0188][0189][0190]
将式(32)和(33)代入式(23)中，并进一步代入式(13)中，可得：
[0191][0192]
当γ in＝0且k＝0时，则方程式(34)可简化为：
[0193][0194]
将上式中的指数函数和正弦函数进行傅里叶展开，有1 2τsint＝1-iτe
it
iτe-it
[0195]
由于e-ax
在[0,π]内不是周期性函数，因此它的傅里叶级数在[0,π]内无法收敛，故将函数延伸至[-π,π]区间进行展开，并且只关注x≥0的区间。因此，对指数函数进行偶函数周期展开，并且当γ in≠0且k≠0时，有：
[0196]
[0197]
对于γ in＝0且k＝0时，有：
[0198][0199]
其中，
[0200]
是指数函数的傅里叶系数。针对ε
kn
项的系数进行整理，可得：
[0201][0202]
对于γ in＝0且k＝0时，有：
[0203][0204]
对于α≠0时，上述方程式(39)和(40)组成了一个线性系统，该系统中的h
jn
是一个空间变化的刚度参数，且考虑了各个空间模态之间的耦合效应。
[0205]
因为本发明主要研究耳蜗力学系统的稳定性，我们主要求解式(39)和(40)中的周期性的解，即当re{γ}＝0时的情况。此外，对于稳定性边界的求解，参数γ有两类取值情况，第一类是γ＝0，对应了系统的谐波解；第二类是γ＝1/2*i，对应了系统的分谐波解。为了保证h(x,t)在实数范围内取值，引入了条件其中头上带横线的h表示h的共轭复数。为了确保解的偶函数空间对称性，有：
[0206][0207][0208]
针对解(16)，有如下周期性条件：
[0209]
u(x,t 2πn)＝e
γ(t 2πn)
p(x,t)＝ξnu(x,t)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(43)
[0210]
对于任何正整数n，当ξ＝e
γ2π
且t取固定值时，上述条件满足。当n-》∞时，如果|ξ|《1，这解是稳定的，如果|ξ|》1，解是非稳定的。当ξ＝
±
1时，对应了周期性的解从稳定到非稳定状态的边界条件。如果γ＝0，则ξ＝1,并且有：
[0211]
u(x,t 2π)＝u(x,t)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(44)
[0212]
上式为以2π为周期的谐波解。如果γ＝1/2*i，则ξ＝-1,并且有：
[0213]
u(x,t 2π)＝-u(x,t),u(x,t 4π)＝u(x,t)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(45)
[0214]
上式为双周期的分谐波解。为了对式(39)-(42)进行求解，我们对系统方程进行缩减，另n＝0,1,...,n,且k＝1,2,...,m，通过矩阵表示，可得：
[0215]
[0216]
其中，
[0217]
上述方程总共有2*m*(n 1)个待求解未知系数，a和b为斜对角矩阵。斜对角矩阵a可表示为a＝diag(a0，a1，...，an)，并且有以下形式：
[0218][0219]
其中，
[0220][0221]
三角形斜对角矩阵b有如下形式：
[0222][0223]
其中，
[0224][0225]
a和b矩阵都已知，式(46)问题的求解可以看作是一个特征值问题，即：
[0226][0227]
其中，上述方程中的稳定性解的特征值为1/τ。针对本文讨论的物理问题，我们只关注那些τ为实数且小于1/2的数值，这样才能确保刚度函数k(s,t)为实数且为非负。
[0228]
当基底膜的刚度函数中τ＝0时，刚度函数为非周期性函数，方程的解是稳定的，且解的傅里叶系数满足：
[0229]
[0230]
当k＝0有：
[0231]
式(54)中，φ＝ν2/κ＝π3μ2/(ρσl3)，它表示流体粘性阻力相对于基底膜弹性力的比值。上述方程可简单表示为其中t矩阵依赖于参数φ、γ和α。系统存在非奇异解的条件是满足det(t)＝0，当给定φ和α时，通过求解可得到γ。
[0232]
令α＝1，m＝20，分别计算了两种情况φ＝1*10-8
，1*10-4
下的γ，计算结果如图2所示。其中粗线表示实部解，细线表示虚部解，实部和虚部的交叉点对应了系统的共振模态。
[0233]
由图2可知，实部和虚部的交叉点位置永远为负，这表示解是稳定的。对于相当较小的φ，主要模态的im{γ}都是非零的，因此解是振荡的。当φ增加至1*10-4
时，流体粘度影响增加，主要模态呈现衰减，并无振荡。在以上两种情况，系统模态都是随着时间的增加逐渐衰减，因此，当τ＝0时，周期性的解或者非稳定的解不存在，必须在刚度函数中考虑时间变化效应的非零τ参数，才存在周期性的解。
[0234]
当考虑τ≠0时，基底膜的刚度函数相当于引入了一个随时间变化的内在的调解机制，这个机制的作用效果等同于考虑基底膜的生物活性，即基底膜的材料会随着时间发生变化，且有自我修复性。通过求解式(39)和(40)可得到τ以及对应的特征矢量，在此基础上，通过式(20)求解出周期性的解h(x,t)，计算中选取的参数见表1。
[0235]
表1人耳耳蜗系统计算的参数
[0236]
[0237][0238]
根据表1中的参数，分别计算了当频率ω＝400,1000,2000,5000时的基底膜的竖向位移曲线h(x,t
peak
)，其中t
peak
表示竖向位移取最大值时对应的时刻，计算结果如图3所示。图中的曲线结果为无因次结果，包络线是通过计算基底膜复函数确定，其中复函数的实部位基底膜的振动幅值，虚部为其hilber变换。其中，内部波浪实线表示基底膜的谐波振动，虚线表示基底膜的分谐波振动，外部波浪实线表示基底膜振动的包络曲线
[0239]
本发明采用comsol软件进行仿真。
[0240]
由于外淋巴液具有低粘性，且不可压缩，同时，雷诺数较低，因此，流体选用层流模型，且假定为不可压缩粘性流体，流体的n-s方程为：
[0241][0242]
ρ
▽
·ufluid
＝0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(57)
[0243]
式中，ρ和μ分别为流体的密度和粘度系数，u
fluid
和p分别表示流体的速度和压强，f表示作用在流体上体积力密度。
[0244]
基底膜与外淋巴液接触的界面为流固耦合界面，且有，
[0245]ufluid
＝u
solid
[0246]
σ
·
n＝γ
·
n,γ＝[-p μ(
▽ufluid
(
▽ufluid
)
t
)]
ꢀꢀꢀꢀꢀꢀꢀꢀ
(58)
[0247]
即界面上固体的位移和流体的位移相等，流体运动产生的压力作用在固体上，同时，固体变形产生的应力又反作用于流体上，界面上固体单元节点和流体单元节点保持对应一致，又相互区别。
[0248]
由图3可知，基底膜振动的包络曲线呈现非对称的分布特征，由基底到基顶，曲线幅值先缓慢增加，达到峰值点后，迅速降低。不同的频率下，对应的峰值点位置不同。由此可见，基底膜的行波振动并不一定需要外部主动力来实现，由于基底膜本身刚度随时空的变
化也可以取得与以往纯音激励模型一致的计算结果。
[0249]
图4计算了图3所示的曲线的峰值位置随频率的变化关系，在对数坐标系中进行显示。实心方形是上文计算得到的解析解，空心圆是有限元仿真结果，空心三角形是试验测试结果。由图可知，振动的峰值位置随着频率增加呈现近乎分段线性减少的趋势，频率为2000s-1
的点为分段点，解析结果与数值仿真结果及试验结果均比较吻合，因此说明本发明发展的解析模型是合理且准确的。
[0250]
为了对式(53)进行求解，先考虑一种简单的特殊情况α＝0，即基底膜的刚度函数不依赖于基底膜的位置，因此，傅里叶级数在空间上可以进行解耦，对于每一个空间波数k而言，有：
[0251][0252]
式(56)可简单表示为：
[0253][0254]
其中，对于每一个k，有：
[0255][0256][0257]
其中，d
kn
通过式(50)确定。选取参数ω＝900,1000,1100s-1
，且τ＝0.1,0.2，其他参数参见表1，计算得到不同参数下基底膜的幅值，如图4所示。
[0258]
由图5可知(其中α＝0，k＝1)，当τ＝0.1时，对于ω等于900s-1
和1100s-1
时，基底膜振动是稳定的，即随着时间的增加，基底膜发现近乎等幅的振动，在结束时刻发生了微小的衰减，而对于ω等于1000s-1
时，随着时间的增加，基底膜的振幅逐渐增大，并在结束时刻发生共振。当τ＝0.2时，仅ω等于900s-1
时，基底膜振动是稳定的，在其他频率下，基底膜发生了共振现象。对比两种情况，在ω等于1000s-1
时，基底膜都出现共振，且幅值最大，其他频率下的幅值相对较小。
[0259]
本发明建立的有限元数值仿真结果与解析模型结果较为一致(见图3、4和图9)，且由于考虑了基底膜的材料随时间的变化的效应，共同发现了基底膜存在非稳定的共振运动特征。所不同的是，解析模型未考虑外部激励作用，仅通过基底膜刚度参数的周期性变化调制引起基底膜产生非稳定的整体性共振现象，而有限元模型不仅考虑了材料本身的性质随时间变化，还考虑了外部的激励的时间变化因素，这意味着仅通过基底膜本身的生物活性的变化可使得基底膜感知不同频率的声音，从而产生不同的振动幅值和振动形式。
[0260]
继续分析α≠0的情况，即基底膜刚度在空间位置上是耦合的，且随着长度的变化呈现指数变化。针对选取不同的参数ω(400,600,800s-1
)和τ(0.05,0.08,0.1)，计算了基底膜的随时间变化的振动幅值曲线，如图6-图8所示。
[0261]
由图可知，当τ＝0.05时，基底膜的振动随着时间的增加逐渐衰减，但是刚度的产生的内力变化还无法显著引起基底膜振动的不稳定性。当τ增加至0.08时，基底膜的振动的不稳定性明显加强，且保持周期性的波动。当τ增加至0.1时，基底膜的不稳定性振动非常剧烈。
[0262]
综上分析，刚度参数的时间变化效应体现在频率ω和周期性的幅值参数τ，随着频率和幅值参数的变化，会引起基底膜发生剧烈的共振，从而可引发耳蜗的灵敏的主动听觉过程和放大声音过程。基底膜产生的共振现象会随着周期性的幅值参数τ的增大而越显剧烈，而在低频下的共振现象较中高频时更加显著。而基底膜刚度在空间和时间上的参数变化来源于基底膜结构本身的材料的空间分布性和生物活性，而并非来源于受到外部反馈力作用，即通过基底膜材料内在的属性
‑‑
生物活性实现了基底膜的振动感音放大过程。
[0263]
基于建立的有限元模型，计算了不同激励频率下基底膜的沿y方向位移随空间的变化关系，如图a-3所示。图中选取了高频15000s-1
、中频5000s-1
,1000s-1
,以及低频500s-1
和200s-1
。由图可知，当激励频率由高频逐渐减少至低频时，基底膜的最大位移大体上沿着基底部向顶部进行延伸，然而，当频率降低至500s-1
时，基底膜的振动形式跟以往行波振动(仅在局部产生剧烈振动)发生不同，基底膜不仅在局部出现峰值，且沿着整个空间发生共振现象，当频率继续降低至200s-1
时，基底膜整体产生较为剧烈的共振现象，这也诠释了以往行波理论无法描述的试验现象，即基底膜低频下会产生与行波振动不同的共振现象。
[0264]
基于建立的有限元模型，计算了不同激励频率下基底膜的沿y方向位移随空间的变化关系，如图a-3所示。图中选取了高频15000s-1
、中频5000s-1
,1000s-1
,以及低频500s-1
和200s-1
。由图可知，当激励频率由高频逐渐减少至低频时，基底膜的最大位移大体上沿着基底部向顶部进行延伸，然而，当频率降低至500s-1
时，基底膜的振动形式跟以往行波振动(仅在局部产生剧烈振动)发生不同，基底膜不仅在局部出现峰值，且沿着整个空间发生共振现象，当频率继续降低至200s-1
时，基底膜整体产生较为剧烈的共振现象，这也诠释了以往行波理论无法描述的试验现象，即基底膜低频下会产生与行波振动不同的共振现象。
[0265]
本发明建立考虑了基底膜的刚度参数随空间和时间周期性变化的特征(生物活性)的生物力学模型，不仅重现了以往试验的基底膜行波振动行为，验证了模型的正确性。而且还发现了基底膜存在非稳定的共振现象，通过解析和数值仿真的计算和分析得到以下结论：
[0266]
(1)当基底膜的刚度不存在时间变化效应，即当τ＝0时，基底膜的振动是稳定的，由于考虑了流体的粘性，基底膜的振动随着时间的增加是逐渐衰减的。当基底膜存在生物活性，即当τ≠0时，基底膜的振动变成非稳定的，且呈现周期性的振动特征。
[0267]
(2)在大于等于400s-1
频率范围时，基底膜的振动呈现行波的振动特性，随着刚度的频率参数的增加，基底膜的最大振幅逐渐从基顶向基底偏移，由于流体的粘性和基底膜本身的阻尼，振幅逐渐减少。当频率小于400s-1
时，基底膜振动形式跟以往行波振动(仅在局部产生剧烈振动)发生不同，基底膜不仅在局部出现峰值，且沿着整个空间发生共振现象，当频率为200s-1
时，基底膜整体产生较为剧烈的共振现象，这也诠释了以往行波理论无法描述的试验现象
[10,39-40]
，即基底膜低频下会产生与行波振动不同的共振现象。
[0268]
(3)当描述基底膜刚度的空间位置变化参数α＝0时，即不考虑时间变化参数与空间变化参数的耦合，在ω等于1000s-1
时，不管时间参数τ＝0.1或0.2时，基底膜均发生非稳定的共振现象，其他频率下的幅值较小。仅当时间参数τ逐渐增大时，基底膜才会在其他频率下发生稳定性的共振运动。
[0269]
(4)当α≠0时，即基底膜刚度在空间位置上是耦合的，基底膜在不同的频率下均发生非稳定的振动，且随着τ的增加，基底膜的非稳定振动变得剧烈，伴随发生共振现象。
[0270]
通过本发明研究，得到一个重要结论：未考虑外部激励作用，仅通过基底膜刚度参数在时间和空间的周期性变化调制，会引起基底膜产生非稳定的整体性共振现象，从而引发耳蜗灵敏的感知和放大声音过程，这暗示着无须通过附加力作用，仅通过基底膜本身的生物活性的变化可使得基底膜与周围淋巴液产生剧烈的耦合振动，(也就是说，耳蜗对声音的放大机制中有一部分来源于基底膜及其微观组织结构本身的生物活性，这个观点在以往的研究中未接报道。)本计算模型可以帮助人类全面的揭示耳蜗对声音的放大机理。
[0271]
由本发明的研究成果可以推断得到一个重要结论：应用物理力学原理建模分析生命体，应该突破以往研究物体的经典理论方法，补充计入生命体的生物活性的变化，这是生物力学与一般力学的本质差异。
[0272]
本发明为应用物理力学原理建模分析生命体提供了准确、可行且高效的计算方法。
[0273]
对于本领域技术人员而言，显然本发明不限于上述示范性实施例的细节，而且在不背离本发明的精神或基本特征的情况下，能够以其他的具体形式实现本发明。因此，无论从哪一点来看，均应将实施例看作是示范性的，而且是非限制性的，本发明的范围由所附权利要求而不是上述说明限定，因此旨在将落在权利要求的等同要件的含义和范围内的所有变化囊括在本发明内。不应将权利要求中的任何附图标记视为限制所涉及的权利要求。
[0274]
此外，应当理解，虽然本说明书按照实施方式加以描述，但并非每个实施方式仅包含一个独立的技术方案，说明书的这种叙述方式仅仅是为清楚起见，本领域技术人员应当将说明书作为一个整体，各实施例中的技术方案也可以经适当组合，形成本领域技术人员可以理解的其他实施方式。