基于几何代数的多环耦合机构奇异分析方法及系统

1.本发明涉及多环耦合机构奇异分析的技术领域，具体地，涉及基于几何代数的多环耦合机构奇异分析方法及系统，尤其涉及基于几何代数的等效支链的多环耦合机构奇异分析方法及系统。


背景技术：

2.并联机构属于多环闭链机构，奇异是并联机构的一个重要的机构学特性，当机构发生奇异时，机构运动约束条件在奇异位形下发生线性相关而失效，机构的自由度发生瞬变。机构处于奇异位形，或在奇异位形附近区域时，其传递性能会变差，机构动平台变得不可控。在涉及和应用并联机器人时应避开奇异位形。所以，分析机构的奇异位形对并联机构的设计，轨迹规划及驱动控制至关重要。
3.机构的奇异分析方法大致可以分为两种，分别是代数法和几何法。几何法主要是分析并联机构雅可比矩阵的秩来判断奇异。雅可比矩阵代表驱动关节速度与末端执行器速度之间的映射关系，当雅可比矩阵行列式为0时则产生奇异。gosselin和 angeless把并联机器人雅可比矩阵拆分为与运动学正解和运动学逆解相关的两部分。黄真等人通过运用螺旋的方法建立雅可比矩阵，分析其传递力螺旋与约束力螺旋产生线性相关时雅可比矩阵行列式为0来判断机构奇异。代数法是一种经典的传统的方法，但是对于结构复杂的并联机构，其雅可比矩阵行列式是一个复杂的非线性方程，要求得满足其为0的符号解十分困难，而且很难表示出其代表的几何意义。几何法的本质是通过分析并联机构中运动关节的运动矢量和约束矢量的线性相关性来判断奇异。hunt运用螺旋理论研究并联机构的奇异。merlet提出了基于grassmann 线几何的方法分析奇异。amine也应用grassmann-cayley代数的方法分析奇异。几何法可以直观的表示出机构奇异的几何条件，但是对于复杂的多环耦合机构，应用几何法的难度也很大。
4.近年来，机构的结构开始向更为复杂的空间结构发展，并联机构从简单的开环支链逐渐向多环耦合机构发展，多环耦合机构不仅具有并联机构承载能力强、精度高等优点，还具有串联机构工作空间大、控制灵活等优点。多环耦合机构包括复杂的，耦合的，封闭的子链，从而导致其拥有复杂的运动学关系，例如一些折展机构，变魔方机构，传统的奇异分析方法在处理这些机构时存在分析过程复杂，计算过程较为繁琐等不足，所以提出一种高效，简洁的计算多环耦合机构奇异分析的方法是十分必要的。
5.因此，需要提出一种新的技术方案以改善上述技术问题。


技术实现要素：

6.针对现有技术中的缺陷，本发明的目的是提供一种基于几何代数的多环耦合机构奇异分析方法及系统。
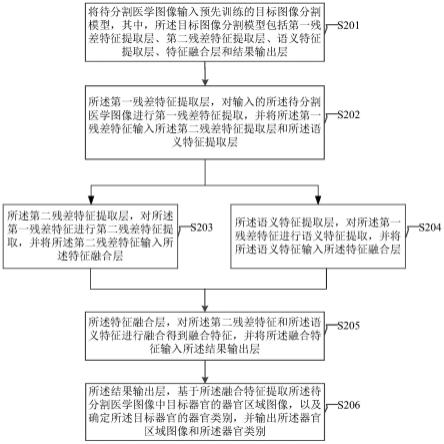
7.根据本发明提供的一种基于几何代数的多环耦合机构奇异分析方法，所述方法包括如下步骤：
8.步骤s1：选定机构的定平台和动平台，划分基础分支，写出每个基础分支上运动副的运动螺旋，计算每个基础分支的分支运动空间，计算每个基础分支的约束空间；
9.步骤s2：找出与基础分支形成闭环的所有耦合支链，写出每个耦合支链上运动副的运动螺旋，计算耦合支链上的分支运动空间，计算耦合支链的约束空间；
10.步骤s3：判断闭环中耦合支链的约束空间是否属于闭环中基础支链的约束空间，判断方法为：将闭环中耦合支链的约束空间和闭环中基础支链的约束空间求外积运算；
11.步骤s4：若步骤s3中外积运算结果为0，则说明闭环中两条支链的约束空间线性相关，则将闭环中基础支链的约束空间等效为闭环的约束空间；若步骤s3中外积运算结果不为0，则将基础支链和耦合支链的约束空间的并集等效为闭环输出的约束空间；
12.步骤s5：对所有包含闭环的基础分支进行以上步骤计算；
13.步骤s6：去除将闭环等效后每个新的等效分支上冗余和相同的约束螺旋，计算所有等效支链的约束空间的外积，得到外积系数，令外积系数为0得到机构的奇异位形。
14.优选地，所述步骤s1与步骤s2中，螺旋在六维几何代数g6中表示为一个一维片积：
15.s＝v1e1 v2e2 v3e3 b1e4 b2e5 b3e616.其中e1,e2,
…
,e6表示g6中的基底，标量系数vi和bi，i＝1,2,3，表示运动副轴线的 pl
ü
cker坐标。
17.优选地，第i个分支上的所有n个运动螺旋做外积运算张成的片积s
mi
表示该分支的运动空间：
18.s
mi
＝s
i1
∧s
i2
∧
…
∧s
in
19.其中s
ij
(j＝1,
…
,n)表示第i个分支上的第j个运动副的运动螺旋，“∧”表示外积运算符号；
20.第i个分支施加到动平台上的分支约束空间记为s
ci
：
[0021][0022]
其中表示g6中的单位伪标量的逆，“δ”表示直射变换算子，其运算为交换表示螺旋的主部系数vi和副部系数bi。
[0023]
优选地，所述步骤s3与步骤s4中，等效支链的处理方法为：
[0024]
确定基础分支后，找出闭环中与基础分支耦合的耦合支链，第i个基础分支的约束空间为s
ci
，与第i个基础分支耦合的耦合支链约束空间为s
ci1
,s
ci2
,
…
,s
cij
，计算闭环上每个分支的约束空间的外积，表示为：
[0025]sci
∧s
cij
[0026]
优选地，若外积结果为0，说明两个分支的约束空间线性相关，则用其一条分支等效代替闭环结构进行奇异分析；
[0027]
若外积结果不为0，将约束空间分解为约束子空间，判断和去除冗余的约束子空间，将线性不相关的约束子空间作并集，代替闭环的约束空间。
[0028]
本发明还提供一种基于几何代数的多环耦合机构奇异分析系统，所述系统包括如下模块：
[0029]
模块m1：选定机构的定平台和动平台，划分基础分支，写出每个基础分支上运动副的运动螺旋，计算每个基础分支的分支运动空间，计算每个基础分支的约束空间；
[0030]
模块m2：找出与基础分支形成闭环的所有耦合支链，写出每个耦合支链上运动副的运动螺旋，计算耦合支链上的分支运动空间，计算耦合支链的约束空间；
[0031]
模块m3：判断闭环中耦合支链的约束空间是否属于闭环中基础支链的约束空间，判断方法为：将闭环中耦合支链的约束空间和闭环中基础支链的约束空间求外积运算；
[0032]
模块m4：若模块m3中外积运算结果为0，则说明闭环中两条支链的约束空间线性相关，则将闭环中基础支链的约束空间等效为闭环的约束空间；若模块m3中外积运算结果不为0，则将基础支链和耦合支链的约束空间的并集等效为闭环输出的约束空间；
[0033]
模块m5：对所有包含闭环的基础分支进行以上模块计算；
[0034]
模块m6：去除将闭环等效后每个新的等效分支上冗余和相同的约束螺旋，计算所有等效支链的约束空间的外积，得到外积系数，令外积系数为0得到机构的奇异位形。
[0035]
优选地，所述模块m1与模块m2中，螺旋在六维几何代数g6中表示为一个一维片积：
[0036]
s＝v1e1 v2e2 v3e3 b1e4 b2e5 b3e6[0037]
其中e1,e2,
…
,e6表示g6中的基底，标量系数vi和bi，i＝1,2,3，表示运动副轴线的 pl
ü
cker坐标。
[0038]
优选地，第i个分支上的所有n个运动螺旋做外积运算张成的片积s
mi
表示该分支的运动空间：
[0039]smi
＝s
i1
∧s
i2
∧
…
∧s
in
[0040]
其中s
ij
(j＝1,
…
,n)表示第i个分支上的第j个运动副的运动螺旋，“∧”表示外积运算符号；
[0041]
第i个分支施加到动平台上的分支约束空间记为s
ci
：
[0042][0043]
其中表示g6中的单位伪标量的逆，“δ”表示直射变换算子，其运算为交换表示螺旋的主部系数vi和副部系数bi。
[0044]
优选地，所述模块m3与模块m4中，等效支链的处理系统为：
[0045]
确定基础分支后，找出闭环中与基础分支耦合的耦合支链，第i个基础分支的约束空间为s
ci
，与第i个基础分支耦合的耦合支链约束空间为s
ci1
,s
ci2
,
…
,s
cij
，计算闭环上每个分支的约束空间的外积，表示为：
[0046]sci
∧s
cij
[0047]
优选地，若外积结果为0，说明两个分支的约束空间线性相关，则用其一条分支等效代替闭环结构进行奇异分析；
[0048]
若外积结果不为0，将约束空间分解为约束子空间，判断和去除冗余的约束子空间，将线性不相关的约束子空间作并集，代替闭环的约束空间。
[0049]
与现有技术相比，本发明具有如下的有益效果：
[0050]
1、本发明计算过程简单，本发明的奇异分析方法只需确定多环耦合机构闭环分支的运动螺旋即可进行分支约束空间的计算，操作简单；
[0051]
2、本发明物理意义清晰，本发明应用几何代数求解约束空间，将多环耦合机构闭环的约束空间等效为新的基础分支的约束空间，相当于将多环耦合机构进行解耦等效为开链分支的并联机构，分析过程简单。
附图说明
[0052]
通过阅读参照以下附图对非限制性实施例所作的详细描述，本发明的其它特征、目的和优点将会变得更明显：
[0053]
图1为本发明等效支链奇异分析方法的流程图；
[0054]
图2为本发明实施例的bennett机构简图；
[0055]
图3为本发明实施例的twin-bennett机构简图；
[0056]
图4为本发明实施例的twin-bennett机构图；
[0057]
图5为本发明实施例的关节坐标系位置图；
[0058]
图6为本发明实施例的twin-bennett机构的运动螺旋图。
具体实施方式
[0059]
下面结合具体实施例对本发明进行详细说明。以下实施例将有助于本领域的技术人员进一步理解本发明，但不以任何形式限制本发明。应当指出的是，对本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变化和改进。这些都属于本发明的保护范围。
[0060]
实施例1：
[0061]
根据本发明提供的一种基于几何代数的多环耦合机构奇异分析方法，方法包括如下步骤：
[0062]
步骤s1：选定机构的定平台和动平台，划分基础分支，写出每个基础分支上运动副的运动螺旋，计算每个基础分支的分支运动空间，计算每个基础分支的约束空间；
[0063]
步骤s2：找出与基础分支形成闭环的所有耦合支链，写出每个耦合支链上运动副的运动螺旋，计算耦合支链上的分支运动空间，计算耦合支链的约束空间；
[0064]
步骤s1与步骤s2中，螺旋在六维几何代数g6中表示为一个一维片积：
[0065]
s＝v1e1 v2e2 v3e3 b1e4 b2e5 b3e6[0066]
其中e1,e2,
…
,e6表示g6中的基底，标量系数vi和bi，i＝1,2,3，表示运动副轴线的 pl
ü
cker坐标。
[0067]
第i个分支上的所有n个运动螺旋做外积运算张成的片积s
mi
表示该分支的运动空间：
[0068]smi
＝s
i1
∧s
i2
∧
…
∧s
in
[0069]
其中s
ij
(j＝1,
…
,n)表示第i个分支上的第j个运动副的运动螺旋，“∧”表示外积运算符号；
[0070]
第i个分支施加到动平台上的分支约束空间记为s
ci
：
[0071][0072]
其中表示g6中的单位伪标量的逆，“δ”表示直射变换算子，其运算为交换表示螺旋的主部系数vi和副部系数bi。
[0073]
步骤s3：判断闭环中耦合支链的约束空间是否属于闭环中基础支链的约束空间，判断方法为：将闭环中耦合支链的约束空间和闭环中基础支链的约束空间求外积运算；
[0074]
步骤s4：若步骤s3中外积运算结果为0，则说明闭环中两条支链的约束空间线性相
关，则将闭环中基础支链的约束空间等效为闭环的约束空间；若步骤s3中外积运算结果不为0，则将基础支链和耦合支链的约束空间的并集等效为闭环输出的约束空间；
[0075]
步骤s3与步骤s4中，等效支链的处理方法为：
[0076]
确定基础分支后，找出闭环中与基础分支耦合的耦合支链，第i个基础分支的约束空间为s
ci
，与第i个基础分支耦合的耦合支链约束空间为s
ci1
,s
ci2
,
…
,s
cij
，计算闭环上每个分支的约束空间的外积，表示为：
[0077]sci
∧s
cij
[0078]
若外积结果为0，说明两个分支的约束空间线性相关，则用其一条分支等效代替闭环结构进行奇异分析；
[0079]
若外积结果不为0，将约束空间分解为约束子空间，判断和去除冗余的约束子空间，将线性不相关的约束子空间作并集，代替闭环的约束空间。
[0080]
步骤s5：对所有包含闭环的基础分支进行以上步骤计算；
[0081]
步骤s6：去除将闭环等效后每个新的等效分支上冗余和相同的约束螺旋，计算所有等效支链的约束空间的外积，得到外积系数，令外积系数为0得到机构的奇异位形。
[0082]
实施例2：
[0083]
实施例2为实施例1的优选例，以更为具体地对本发明进行说明。
[0084]
本发明还提供一种基于几何代数的多环耦合机构奇异分析系统，系统包括如下模块：
[0085]
模块m1：选定机构的定平台和动平台，划分基础分支，写出每个基础分支上运动副的运动螺旋，计算每个基础分支的分支运动空间，计算每个基础分支的约束空间；
[0086]
模块m2：找出与基础分支形成闭环的所有耦合支链，写出每个耦合支链上运动副的运动螺旋，计算耦合支链上的分支运动空间，计算耦合支链的约束空间；
[0087]
模块m1与模块m2中，螺旋在六维几何代数g6中表示为一个一维片积：
[0088]
s＝v1e1 v2e2 v3e3 b1e4 b2e5 b3e6[0089]
其中e1,e2,
…
,e6表示g6中的基底，标量系数vi和bi，i＝1,2,3，表示运动副轴线的 pl
ü
cker坐标。
[0090]
第i个分支上的所有n个运动螺旋做外积运算张成的片积s
mi
表示该分支的运动空间：
[0091]smi
＝s
i1
∧s
i2
∧
…
∧s
in
[0092]
其中s
ij
(j＝1,
…
,n)表示第i个分支上的第j个运动副的运动螺旋，“∧”表示外积运算符号；
[0093]
第i个分支施加到动平台上的分支约束空间记为s
ci
：
[0094][0095]
其中表示g6中的单位伪标量的逆，“δ”表示直射变换算子，其运算为交换表示螺旋的主部系数vi和副部系数bi。
[0096]
模块m3：判断闭环中耦合支链的约束空间是否属于闭环中基础支链的约束空间，判断方法为：将闭环中耦合支链的约束空间和闭环中基础支链的约束空间求外积运算；
[0097]
模块m4：若模块m3中外积运算结果为0，则说明闭环中两条支链的约束空间线性相
关，则将闭环中基础支链的约束空间等效为闭环的约束空间；若模块m3中外积运算结果不为0，则将基础支链和耦合支链的约束空间的并集等效为闭环输出的约束空间；
[0098]
模块m3与模块m4中，等效支链的处理系统为：
[0099]
确定基础分支后，找出闭环中与基础分支耦合的耦合支链，第i个基础分支的约束空间为s
ci
，与第i个基础分支耦合的耦合支链约束空间为s
ci1
,s
ci2
,
…
,s
cij
，计算闭环上每个分支的约束空间的外积，表示为：
[0100]sci
∧s
cij
[0101]
若外积结果为0，说明两个分支的约束空间线性相关，则用其一条分支等效代替闭环结构进行奇异分析；
[0102]
若外积结果不为0，将约束空间分解为约束子空间，判断和去除冗余的约束子空间，将线性不相关的约束子空间作并集，代替闭环的约束空间。
[0103]
模块m5：对所有包含闭环的基础分支进行以上模块计算；
[0104]
模块m6：去除将闭环等效后每个新的等效分支上冗余和相同的约束螺旋，计算所有等效支链的约束空间的外积，得到外积系数，令外积系数为0得到机构的奇异位形。
[0105]
实施例3：
[0106]
实施例3为实施例1的优选例，以更为具体地对本发明进行说明。
[0107]
本发明提出一种使用几何代数这种数学工具，基于等效支链的多环耦合机构奇异分析方法，该方法具有分析过程简洁，计算过程方便的特点。
[0108]
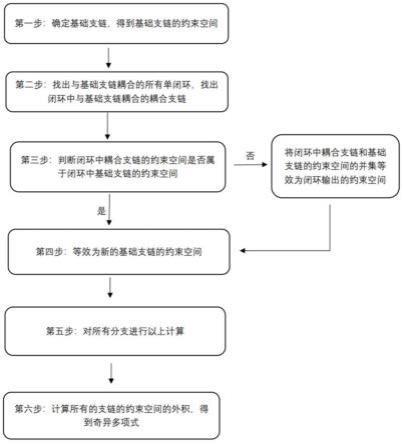
本发明提供一种基于几何代数的等效支链的多环耦合机构奇异分析方法，按以下步骤进行：
[0109]
步骤一：选定机构的定平台和动平台，划分基础分支，写出每个基础分支上运动副的运动螺旋，得到每个基础分支的分支运动空间，进而得到每个基础分支的约束空间；
[0110]
螺旋在六维几何代数g6中表示为一个一维片积：
[0111]
s＝v1e1 v2e2 v3e3 b1e4 b2e5 b3e6[0112]
其中e1,e2,
…
,e6表示g6中的基底，标量系数vi和bi(i＝1,2,3)表示运动副轴线的 pl
ü
cker坐标。
[0113]
第i个分支上的所有n个运动螺旋做外积运算张成的片积s
mi
表示该分支的运动空间：
[0114]smi
＝s
i1
∧s
i2
∧
…
∧s
in
[0115]
其中s
ij
(j＝1,
…
,n)表示第i个分支上的第j个运动副的运动螺旋，“∧”表示外积运算符号。
[0116]
第i个分支施加到动平台上的分支约束空间可以记为s
ci
,可以将运动空间s
mi
通过对偶和直射变换共同运算得出，表示为：
[0117][0118]
表示将运动空间s
mi
进行对偶运算，其中表示g6中的单位伪标量的逆，“δ”表示直射变换算子，其运算为交换表示螺旋的主部系数vi和副部系数bi, 螺旋的物理含义表示为构成运动空间和力空间的元素，可以用直射变换δ实现两个空间的转化。
[0119]
步骤二：找出闭环中与基础分支耦合的所有耦合支链，写出每个耦合支链上运动副的运动螺旋，计算耦合支链上的分支运动空间，计算耦合支链上的约束空间；
[0120]
闭环中与第i个基础分支耦合的耦合支链的分支运动空间s
′
mij
表示为：
[0121]s′
mij
＝s
′
ij1
∧s
′
ij2
∧
…
∧s
′
ijn
[0122]
其中s
′
mij
(j＝1,
…
,n)表示与第i个基础分支耦合的第j个耦合支链的运动空间， s
′
ijk
(k＝1,
…
,n)表示与第i个基础分支耦合的第j个闭环分支上第k个的运动副的运动螺旋；
[0123]
步骤三：判断闭环中与基础分支耦合的耦合支链的约束空间是否属于闭环中基础分支的约束空间，判断方法为将闭环中与基础分支耦合的耦合支链的约束空间和闭环中基础分支的约束空间求外积，对外积结果进行讨论；
[0124]
确定基础分支后，找出与基础分支耦合的耦合支链，第i个基础分支的约束空间为 s
ci
，与第i个基础分支耦合的耦合支链约束空间为s
ci1
,s
ci2
,
…
,s
cij
，计算闭环上基础分支和耦合支链的约束空间的外积，表示为：
[0125]sci
∧s
cij
[0126]
步骤四：若步骤三中外积运算结果为0，则说明闭环中两条支链的约束空间线性相关，则将闭环中基础支链的约束空间等效为闭环的约束空间；若步骤三中外积运算结果不为0，则将基础支链和耦合支链的约束空间的并集等效为闭环输出的约束空间；
[0127]
具体等效支链的处理方法为：
[0128]
若外积结果为0，说明两个分支的约束空间线性相关，则可用基础分支的约束空间为s
ci
等效代替闭环结构的约束空间进行奇异分析；
[0129]
若外积结果不为0，将基础分支的约束空间s
ci
和与基础分支耦合的耦合支链的约束空间s
ci1
,s
ci2
,
…
,s
cij
求并集，以此并集等效替换为闭环输出的约束空间。
[0130]
求并集的方法为：将约束空间s
ci
和s
cij
分解为只由1阶片积组成的约束子空间，判断和去除冗余的约束子空间，将线性不相关的约束子空间作并集，以此代替闭环的约束空间。
[0131]
步骤五：对所有包含闭环的基础分支进行以上步骤计算；
[0132]
步骤六：去除将闭环等效后每个新的等效分支上冗余和相同的约束螺旋，计算所有等效支链的约束空间的外积，得到外积系数，令外积系数为0得到机构的奇异位形。
[0133]
本发明提出等效支链分析奇异的方法，通过基于几何代数计算闭环上每个分支的约束空间，计算闭环上每个分支的约束空间之间的外积，判断分支约束空间之间的线性相关性，若外积结果为0，说明两个分支的约束空间线性相关，则可用其一条分支等效代替闭环结构的约束空间进行奇异分析；若外积结果不为0，将约束空间分解为约束子空间，判断和去除冗余的约束空间，将线性不相关的约束子空间作并集，以此代替闭环的约束空间进行奇异分析。最后对所有的将闭环等效后的分支的约束空间求并集，得到外积系数，令外积系数为0得到机构的奇异位形。
[0134]
twin-bennett闭环机构奇异分析：
[0135]
bennett机构是唯一的由4个转动副构成的单自由度空间机构，它在机构学理论上的地位非常重要，是公认的最经典的过约束机构，杆件数目最少，约束度最高的，并且有很多机构是以bennett机构作为单元进行综合得到的。bennett机构作为单自由度空间单环路
机构(图2为该机构简图)，由四个连杆和四个转动副组成。四个转动副的中心点分别为a、b、c、d位置相对的连杆具有相同的性质。四个连杆长度分别为 ab＝cd＝m和ad＝ba＝n，ab杆，cd杆，ad杆和bc杆两端转动副轴线相对的扭转角分别记为α
ab
,α
dc
,α
ad
和α
bc
,且α
ab
＝α
dc
＝α，α
ad
＝α
bc
＝β。连杆长度和连杆两端转动副轴线相对的扭转角度满足如下关系：
[0136][0137]
取两个相同的bennett机构，两者呈对称布置，通过共同连杆和运动副连接成一个过约束的6r机构，构成twin-bennett机构(图3为该机构简图)，该机构含有6个转动副和7个连杆，twin-bennett机构满足以下几何关系：
[0138]
oa＝cb＝cd＝a
[0139]
oc＝ab＝ad＝b
[0140]
α
oa
＝α
cb
＝α1＝-α，α
cd
＝α2＝α
[0141]
α
oc
＝α
ab
＝α
ad
＝β
[0142][0143][0144][0145]
以转动副6中心点为原点建立如图5所示固定坐标系,其中z轴沿着转动副6轴线杆方向，d杆和x轴的夹角为θ，α表示为3，4转动副的轴线关于z轴的扭转角，β表示1，6转动副之间的扭转角，表示c杆和f杆的夹角，表示c杆和b杆的夹角，m、l表示对应的杆长。
[0146]
将twin-bennett机构以杆e为动平台，转动副6作为驱动副，杆e到机架基础分支为：
[0147][0148]
支链1-a-2-b-3与基础分支6-d-1耦合，形成闭环。
[0149]
机构6个转动副的运动螺旋分别为：
[0150][0151]
基础分支6-d-1的运动空间s
m1
由其上螺旋s1,s6扩展而成：
[0152]sm1
＝s1∧s6[0153]
ꢀꢀ
＝-s(β)s(θ)e
1,3
s(β)c(θ)e
2,3-mc(β)s(θ)e
3,4
mc(β)c(θ)e
3,5-ms(β)e
3,6
[0154]
基础分支6-d-1的约束空间s
c1
可以写成：
[0155][0156]
基础分支4-f-5的运动空间s
m2
由其上螺旋s4,s5扩展而成：
[0157]sm2
＝s4∧s5[0158]
ꢀꢀ
＝s(β)s(θ)s(α)e
1,2,3
s(β)s(θ)lc(α)e
1,3,5-s(β)s(θ)ls(α)e
1,3,6-mc(β)s(θ)s(α)e
2,3,4 (mc(β)c(θ)s(α)-s(β)c(θ)lc(α))e
2,3,5
(s(β)c(θ)ls(α)-ms(β)s(α))e
2,3,6 mc(β)s(θ)lc(α)e
3,4,5-mc(β)s(θ)ls(α)e
3,4,6
(mc(β)c(θ)ls(α)-ms(β)lc(α))e
3,5,6
[0159]
基础分支4-f-5的约束空间s
c2
可以写成：
[0160][0161]
与基础分支6-d-1耦合的分支1-a-2-b-3的运动空间s'
m11
由其上螺旋s1,s2,s3扩展而成：
[0162]
s'
m11
＝s1∧s2∧s3[0163]
ꢀꢀꢀ
＝s(β)s(θ)s(α)e
1,2,3-s(β)s(θ)lc(α)e
1,3,5-s(β)s(θ)ls(α)e
1,3,6-mc(β)s(θ)s(α)e
2,3,4 (mc(β)c(θ)s(α) s(β)c(θ)lc(α))e
2,3,5
(s(β)c(θ)ls(α)-ms(β)s(α))e
2,3,6-mc(β)s(θ)lc(α)e
3,4,5
ꢀ‑
mc(β)s(θ)ls(α)e
3,4,6
(mc(β)c(θ)ls(α) ms(β)lc(α))e
3,5,6
[0164]
闭环分支1-a-2-b-3的约束空间s
c11
可以写成：
[0165][0166]
闭环支链的等效：
[0167]
将耦合分支1-a-2-b-3约束空间进行片积分解，分解成3个一阶片积，得到其3 个约束子空间b1,b2,b3：
[0168]sc11
＝b1∧b2∧b3[0169][0170][0171][0172]
将3个一阶片积b1,b2,b3分别与基础分支6-d-1的约束空间s
c1
进行外积运算：
[0173]sc1
∧b1＝0
[0174]sc1
∧b2＝0
[0175]sc1
∧b3＝0
[0176]
经过计算，链6-d-1的约束空间与链3-b-2-a-1的3个约束子空间的外积均为0，根据几何代数的运算法则，说明两个支链的约束空间是线性相关的，进一步说明，两个支链的约束空间可以相互等效替代，所以对于该机构，将基础分支6-d-1和耦合分支1-a-2-b-3构成的闭环的约束空间，用基础分支6-d-1的约束空间等效计算。
[0177]
所以，一个闭环的约束空间可以用链6-d-1的约束空间等效，令转动副6作为驱动副，锁住驱动副关节s6后，基础分支6-d-1的运动空间的约束空间可以写为：
[0178]sm1
＝s1[0179][0180]
判断和去除冗余约束后，为了分析两条支链的约束空间的线性相关性，对他们进行外积运算得：
[0181][0182]
多项式q包括机构的结构参数，给定机构的结构参数时，机构处于特定的位姿状态下q＝0，当驱动角θ角为0
°
或180
°
时，外积系数为0，机构会处于奇异位置。
[0183]
奇异位置验证：
[0184]
twin-bennett机构是由两个bennett机构，两边呈对称布置，两侧运动情况也与bennett机构的运动情况相同,输入角θ是唯一变量，不同位形下动平台上的运动螺旋如图6所示，
①
线表示不同位形下的动平台上的许动螺旋的方向，
②
线表示许动螺旋上一点的迹线，当θ角为0
°
和180
°
时，运动螺旋方向发生突变，是机构的奇异位置，验证了本发明分析奇异方法的正确性。
[0185]
本领域技术人员可以将本实施例理解为实施例1、实施例2的更为具体的说明。
[0186]
本领域技术人员知道，除了以纯计算机可读程序代码方式实现本发明提供的系统及其各个装置、模块、单元以外，完全可以通过将方法步骤进行逻辑编程来使得本发明提供的系统及其各个装置、模块、单元以逻辑门、开关、专用集成电路、可编程逻辑控制器以及嵌入式微控制器等的形式来实现相同功能。所以，本发明提供的系统及其各项装置、模块、单元可以被认为是一种硬件部件，而对其内包括的用于实现各种功能的装置、模块、单元也可以视为硬件部件内的结构；也可以将用于实现各种功能的装置、模块、单元视为既可以是实现方法的软件模块又可以是硬件部件内的结构。
[0187]
以上对本发明的具体实施例进行了描述。需要理解的是，本发明并不局限于上述特定实施方式，本领域技术人员可以在权利要求的范围内做出各种变化或修改，这并不影响本发明的实质内容。在不冲突的情况下，本技术的实施例和实施例中的特征可以任意相互组合。