利用变距实验测量毕奥-萨伐尔定律中零距离常数的方法与流程

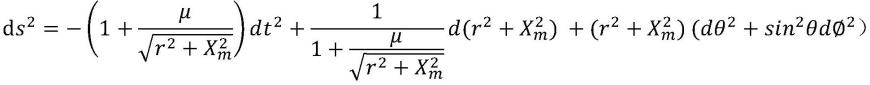
1.本发明涉及一种利用变距实验测量毕奥-萨伐尔定律中零距离常数的方法。


背景技术：

2.在静磁学中，毕奥-萨伐尔定律(英文：biot-savart law)描述电流元在空间任意点p处所激发的磁场。毕奥-萨伐尔定律表示如下：
3.电流元idl在空间某点p处产生的磁感应强度db的大小与电流元idl的大小成正比，与电流元idl所在处到p点的位置矢量和电流元idl之间的夹角的正弦成正比，而与电流元idl到p点的距离r的平方成反比。
[0004][0005]
μ0为真空磁导率；
[0006]
现有的毕奥-萨伐尔定律存在一个明显的缺陷，就是在电流元idl到p点之间的距离趋于零的情况下，磁感应强度db会趋于无穷大，但是，这个结论显然与事实不符，因为p点即使是在电流元idl的原点处，也不可能产生无穷大的磁感应强度db。事实上，即使电流元idl到p点之间之间的距离趋于零，磁感应强度db也只能是趋于一个常数，绝不会是无穷大,换言之，即使在构成电子流的一个个电子所在的原点处，该处的磁感应强度db也只能是一个常数，绝不会是无穷大。因此，修正后的毕奥-萨伐尔定律可表示如下：
[0007]
电流元idl在空间某点p处产生的磁感应强度db的大小与电流元idl的大小成正比，与电流元idl所在处到p点的位置矢量和电流元idl之间的夹角的正弦成正比，而与电流元idl到p点的距离r加上距离修正常数xb的平方成反比，即：
[0008][0009]
式中xb是毕奥-萨伐尔定律的距离修正常数。
[0010]
或者，修正后的毕奥-萨伐尔定律可表示如下：
[0011]
电流元idl在空间某点p处产生的磁感应强度db的大小与电流元idl的大小成正比，与电流元idl所在处到p点的位置矢量和电流元idl之间的夹角的正弦成正比，而与电流元idl到p点的距离r的平方加上距离修正常数xb成反比，即：
[0012][0013]
式中x是毕奥-萨伐尔定律的距离修正常数。
[0014]
需要说明的是，在得到足够精确、足够多的实验数据后，通过插入实验数据进行计算，有可能发现距离修正常数xb不是一个常数，而是变化不定的变数，这表明修正后的二个毕奥-萨伐尔定律的公式都不对，这时候就要根据这一具体情况调继续整毕奥-萨伐尔定律的表达式，直至根据实验数据计算出来的距离修正常数xb非常贴近于一个常数为止，这时候的磁场强度的表达式才是最符合实际状态的、也更加精确的磁场强度计算公式。
[0015]
需要指出的是，毕奥-萨伐尔定律的距离修正常数xb的具体数值是多少，人们在目前并不知道。因此，有必要通过实验测量来得到毕奥-萨伐尔定律中距离修正常数xb的具体数值。


技术实现要素：

[0016]
本发明的目的是提供一种可解决现有的毕奥-萨伐尔定律存在明显的缺陷，精确得到毕奥-萨伐尔定律的距离修正常数，再根据零距离常数进一步得到新的真空磁导率，从而更好的服务于各种涉及计算磁场作用力大小的科技项目的利用变距实验测量毕奥-萨伐尔定律中零距离常数的方法。
[0017]
本发明的利用变距实验测量毕奥-萨伐尔定律中零距离常数的方法，其包括如下步骤：
[0018]
a、设置一个直的长度为dl的长导线，给长导线通上电流强度为i的恒稳电流；
[0019]
b、利用可测量磁感应强度的装置，在长导线附近的空间点p1处测量该处的磁感应强度，得到该处磁感应强度参数b1，利用测距装置测量空间点p1与长导线的中心线之间的距离r1，得到距离参数r1，利用角度测量装置，测量空间点p1与长导线二端连线之间的夹角θ1；
[0020]
c、沿着长导线的垂直方向移动测量磁感应强度的装置，在长导线附近的空间点p2处测量该处的磁感应强度，得到该处磁感应强度参数b2，利用测距装置测量空间点p2与长导线的中心线之间的距离，得到距离参数r2，利用角度测量装置，测量空间点p2与长导线二端连线之间的夹角θ2，所述距离r2为距离r1的2倍以上；
[0021]
d，重复步骤c多次，即利用可测量磁感应强度的装置，在长导线附近的空间点p3、p4、
……
处分别测量该处的磁感应强度，分别得到对应的磁感应强度参数b3、b4、
……
，利用测距装置分别测量空间点p3、p4、
……
与长导线的中心线之间的距离，得到多个距离参数r3、r4、
……
，利用角度测量装置，分别测量空间点p3、p4、p5、
……
与长导线二端连线之间的夹角θ3、θ4、
……
；
[0022]
所述距离r3为距离r2的2倍以上，距离ri为距离ri-1的2倍以上，距离r4为距离r3的2倍以上，
……
；
[0023]
e、根据修正后的毕奥-萨伐尔定律公式：
[0024][0025]
式中xb是毕奥-萨伐尔定律的距离修正常数；
[0026]
将多次测量得到的数据分别代入修正后的毕奥-萨伐尔定律公式，分别得到：
[0027][0028][0029]
[0030][0031]
将上面的4个代入了测量得到的数据的修正后的毕奥-萨伐尔定律公式分别相互进行相除处理，可得到：
[0032]
b1/b2＝[sinθ1/(r1 x)2]/[sinθ2/(r2 xb)2]
ꢀꢀꢀ
(1)
[0033]
b1/b3＝[sinθ1/(r1 x)2]/[sinθ3/(r3 xb)2]
ꢀꢀꢀ
(2)
[0034]
b1/b4＝[sinθ1/(r1 x)2]/[sinθ4/(r4 xb)2]
ꢀꢀꢀ
(3)
[0035]
b2/b3＝[sinθ2/(r2 x)2]/[sinθ3/(r3 xb)2]
ꢀꢀꢀ
(4)
[0036]
b2/b4＝[sinθ2/(r2 x)2]/[sinθ4/(r4 xb)2]
ꢀꢀꢀ
(5)
[0037]
b3/b4＝[sinθ3/(r3 x)2]/[sinθ4/(r4 xb)2]
ꢀꢀꢀ
(6)
[0038]
……
[0039]
根据实验测量到的b1、b2、b3、b4、
……
、θ1、θ2、θ3、θ4、
……
、和r1、r2、r3、r4、
……
计算后，即可得出毕奥-萨伐尔定律中多个距离修正常数xb的具体数值,如果所得到的多个距离修正常数xb不一致，也就是距离修正常数xb是变化不定的变数，这表明修正后的(1)式的修正后的毕奥-萨伐尔定律公式有偏差，则将修正后的毕奥-萨伐尔定律的公式调整为：
[0040][0041]
然后重新利用步骤e进行计算处理，直至根据计算多个实验数据所得到的xe接近于一个常数或者就是一个常数，则该常数xe即为修正后的毕奥-萨伐尔定律中零距离常数xe的具体数值，而与之对应的公式，即为修正后的修正后的毕奥-萨伐尔定律。
[0042]
优选的，所述步骤c中，改变二个物体之间的距离时，让距离ri为距离ri-1的3—20倍。
[0043]
优选的，所述步骤c中，改变二个物体之间的距离时，让距离ri为距离ri-1的5—15倍。
[0044]
优选的，所述步骤c中，改变二个物体之间的距离时，让距离ri为距离ri-1的8—12倍。
[0045]
优选的，所述可测量磁感应强度的装置为便携式磁场测试仪。
[0046]
优选的，所述长导线中的电流强度i大于20安培，所述重复步骤c的次数大于30次。
[0047]
本发明的利用变距实验测量毕奥-萨伐尔定律中零距离常数的方法，其包括如下步骤：设置一个直的长度为dl的长导线，给长导线通上电流强度为i的恒稳电流；在长导线附近的空间点p1处测量该处的磁感应强度，得到该处磁感应强度参数b1，利用测距装置测量空间点p1与长导线的中心线之间的距离r1，得到距离参数r1，利用角度测量装置，测量空间点p1与长导线二端连线之间的夹角θ1。因此，本发明的利用变距实验测量毕奥-萨伐尔定律中零距离常数的方法可解决现有的毕奥-萨伐尔定律存在明显的缺陷，精确得到毕奥-萨伐尔定律的距离修正常数，再根据零距离常数进一步得到新的真空磁导率，从而更好的服务于各种涉及计算磁场作用力大小的科技项目。
[0048]
下面对本发明的利用变距实验测量毕奥-萨伐尔定律中零距离常数的方法的具体实施方式作进一步详细说明。
具体实施方式
[0049]
万有引力定律(law of universal gravitation)是艾萨克
·
牛顿在1687年于《自然哲学的数学原理》上发表的。牛顿的普适的万有引力定律表示如下：
[0050]
任意两个质点m1、m2由通过连心线方向上的力f
12
相互吸引，该引力f
12
大小与它们质量的乘积m1m2成正比，与它们之间距离r的平方成反比，与两物体的化学组成和其间介质种类无关。
[0051][0052]
现有的万有引力定律也存在一个明显的缺陷，就是在两个质点m1、m2之间的距离趋于零的情况下，引力f
12
会趋于无穷大，或者说质点的原点(奇点)所在处的引力场场强是无穷大。但是，这明显与事实不符，也就是说，在两个质点m1、m2之间相距为零时，两个质点m1、m2之间的相互作用力f
12
也不可能是无穷大。事实上，即使两个质点m1、m2之间的距离趋于零，引力f
12
也只能是趋于一个常数，绝不会是无穷大。同样地，如果质点的原点所在处的引力场场强是无穷大，那么，即使离开了质点的原点(奇点)进行检测，该无穷大的引力场场强也不会因为有了距离而有丝毫的递减，其依然只能是无穷大。因此，我们需要在万有引力定律的分母项中插入一个常数，插入的基本原则是让万有引力定律在两个质点m1、m2之间的距离趋于零的情况下，两个质点m1、m2之间的相互作用力f
12
不是无穷大即可，故修正后的万有引力定律、也就是奇点力学下的万有引力定律可表示如下：
[0053]
任意两个质点m1、m2由通过连心线方向上的力f
12
相互吸引，该引力f
12
大小与它们质量的乘积m1m2成正比，与它们之间距离r加上零距离常数x的平方成反比，与两物体的化学组成和其间介质种类无关，即：
[0054][0055]
式中xm是奇点力学下的万有引力定律的零距离常数，我们同时规定，两个质点的体积分别是无穷小，都不能为零。
[0056]
与之对应的，一个质量为m的质点在奇点力学下引力场的场强em为：
[0057][0058]
一个质量为m的质点的奇点力学下引力场的势能um为：
[0059][0060]
对于一个静止的质量为m的质点，在r＝0处，根据质能关系式，可以得到如下关系：
[0061][0062]
整理可得：
[0063][0064]
或者是：g＝xmc2。
[0065]
据此，我们可以将奇点力学下的万有引力定律公式改为以下三种形式：
[0066][0067][0068][0069]
式中的u
m01
＝m1c2，u
m02
＝m2c2。
[0070]
在此需要强调的是，任意两个质点m1、m2之间的距离在奇点力学下就是r xm，或者写成不再是现有知识中的r。也就是说，即使是r＝0，在引力场中，任意两个质点之间也还是有一个xm＝g/c2的常数距离。
[0071]
修正后的奇点力学下的万有引力定律的另一个方案可表示如下：
[0072]
任意两个质点m1、m2由通过连心线方向上的力f
12
相互吸引，该引力f
12
大小与它们质量的乘积m1m2成正比，与它们之间距离r的平方加上零距离常数xm的平方成反比，与两物体的化学组成和其间介质种类无关，即：
[0073][0074]
式中xm是奇点力学下的万有引力定律的零距离常数，我们同时规定，两个质点的体积分别是无穷小，都不能为零。
[0075]
与之对应的，一个质量为m的质点在奇点力学下引力场的场强em为：
[0076][0077]
一个质量为m的质点的奇点力学下引力场的势能um为：
[0078][0079]
对于一个静止的质量为m的质点，在r＝0处，根据质能关系式，可以得到如下关系：
[0080][0081]
整理可得：
[0082][0083]
或者是：g＝xmc2。
[0084]
据此，我们可以将奇点力学下的万有引力定律公式改为以下三种形式：
[0085][0086]
[0087][0088]
式中的u
m01
＝m1c2，u
m02
＝m2c2。
[0089]
在此需要强调的是，任意两个质点m1、m2之间的距离在奇点力学下就是或者写成不再是现有知识中的r。也就是说，即使是r＝0，在引力场中，任意两个质点之间也还是有一个xm＝g/c2的常数距离。
[0090]
我们定义在奇点力学下，如果质点m1、m2是在引力场作用下改变运动状态，则该粒子的运动距离可以采用任意两个质点m1、m2之间的奇点距离r＝r xm＝r g/c2，由此我们得出在奇点力学下的奇点速度概念，即：
[0091]
1、奇点平均速度：在δt时间内，如果两个质点m1、m2之间的数学位移为δr,则其奇点位移为r＝δr xm＝δr g/c2(或者)那么，奇点位移与时刻δt的比值，即为该质点在在δt时间内的奇点平均速度v为：
[0092][0093]
请注意，在δt时间内，当两个质点m1、m2之间的数学位移δr为零时，两个质点m1、m2之间还可以存在一个运动，在这个状态下的奇点平均速度v为：
[0094][0095]
在这种情况下，两个质点m1、m2之间的奇点平均速度v就是一种奇点的内在运动。我们也可以这么看，当两个质点m1、m2之间的数学位移δr为零时，两个质点m1、m2实际上是合并为一个质点，而一个质点的二个部分之间可以存在一种内在的运动，这个运动会趋于让两个质点m1、m2相互分离开，分离所需要的时间间隔δt是：
[0096][0097]
2、奇点瞬时速度v：在dt时间内，如果两个质点m1、m2之间的数学位移为dr,则其奇点位移为r＝δr xm＝δr g/c2(或者)那么，奇点位移与时刻dt的比值，即为该点电荷在在dt时间内的奇点瞬时速度v为：
[0098][0099]
作圆周运动两个质点m1、m2之间的奇点瞬时速度v：
[0100][0101]
上面的ω为质点在奇点力学下的自旋运动。
[0102]
请注意，在dt时间内，当两个质点m1、m2之间的数学位移为δr为零时，奇点力学下作圆周运动的奇点瞬时速度v为：
[0103][0104]
在这种情况下，两个质点m1、m2之间的奇点瞬时速度v就是一种奇点的内在运动。假设内在运动的奇点瞬时速度v为光速c，则又可以得到一个新的常量——奇点力学下的零时间常数dt＝xm/c＝g/c3。
[0105]
在光速下，我们有c＝xmω＝g/c2·
ω。
[0106]
3、奇点瞬时加速度a：
[0107][0108]
4、对于圆周运动，奇点处的向心加速度a：
[0109][0110]
当r＝0时，
[0111][0112]
5、奇点力学下的牛顿第二运动定律：
[0113][0114]
6、奇点力学下的圆周长l的计算公式：
[0115]
l＝2πr＝2π(r xm)＝2π(r g/c2)
[0116]
当r＝0时，
[0117]
l＝2πr＝2πxm＝2πg/c2[0118]
7、奇点力学下的圆面积s的计算公式：
[0119]
s＝πr2＝π(r xm)2＝π(r g/c2)2[0120]
当r＝0时，
[0121][0122]
8、奇点力学下的圆体积d的计算公式：
[0123][0124]
当r＝0时，
[0125][0126]
9、奇点力学下的做功的计算公式：
[0127][0128]
如果则
[0129][0130]
一个质量为m的质点的奇点力学下引力场的势能u为：
[0131][0132]
如果实验证明该质点的在奇点力学下引力场的势能u为：
[0133][0134]
如果实验证明则上面所有的r＝r xm全部换为
[0135]
库仑定律(coulomb's law)是静止点电荷相互作用力的规律，1785年法国科学家c,-a.de库仑由实验得出，库仑定律的常见表述：
[0136]
真空中两个静止的点电荷之间的相互作用力，与它们的电荷量的乘积(q1q2)成正比，与它们的距离(数学距离)的二次方(r2)成反比，作用力的方向在它们的连线上，同性电荷相斥，异性电荷相吸。即：
[0137][0138]
与万有引力定律类似，现有的库伦定律存在一个明显的缺陷，就是在两个点电荷q1、q2之间的距离趋于零的情况下，电场力f
12
会趋于无穷大，但是，这明显与事实不符，也就是说，在两个点电荷q1、q2之间相距为零时，两个点电荷q1、q2之间的相互作用力f
12
也不可能是无穷大。事实上，即使两个点电荷q1、q2之间的距离趋于零，电场力f
12
也只能是趋于一个常数，绝不会是无穷大。因此，需要在库伦定律中插入一个常数，插入的基本原则是让库伦定律在两个点电荷q1、q2之间的距离趋于零的情况下，两个点电荷q1、q2之间的相互作用力f
12
不是无穷大即可，修正后的库伦定律、也就是奇点力学下的库伦定律可表示如下：
[0139]
任意两个点电荷q1、q2由通过连心线方向上的力f
12
相互吸引，该电场力f
12
大小与它们电量的乘积q1q2成正比，与它们之间距离r(数学距离)加上零距离常数xe的平方成反比。即：
[0140][0141]
式中xe是奇点力学下的库伦定律的零距离常数，我们同时规定，两个点电荷q1、q2的体积分别是无穷小，都不能为零。
[0142]
在此需要强调的是，任意两个点电荷q1、q2之间有一个在奇点力学下的奇点距离r，在奇点力学下任意两个点电荷q1、q2之间的奇点距离r就是r xe，不再是现有知识中的数学距离r。也就是说，即使是数学距离r＝0，任意两个点电荷q1、q2之间也还是有一个xe的常数距离。即：对于奇点力学而言，任意两个点电荷q1、q2之间的奇点距离r＝r xe。
[0143]
与之对应的，一个电量为q1的点电荷在奇点力学下电场的场强ee为：
[0144][0145]
一个电量为q1的点电荷的奇点力学下电场的势能ue为：
[0146][0147]
对于一个静止的电量为q1的点电荷，在r＝0处，根据质能关系式，可以得到如下关系：
[0148][0149]
整理可得：
[0150][0151]
或者是：k＝xem
e1
c2/q1。
[0152]
上面的m
e1
是一个静止的电量为q1的点电荷的电磁质量，比例系数
[0153]
据此，我们可以将奇点力学下的一个电量为q1的点电荷的奇点力学下电场的场强ee改为以下三种形式：
[0154][0155][0156][0157]
式中的u
e1
＝m
e1
c2。
[0158]
在此需要强调的是，电场中任意两个点电荷之间的距离在奇点力学下就是r xe，不再是现有知识中的r。也就是说，即使是r＝0，任意两个质点之间也还是有一个
[0159][0160]
的常数距离。
[0161]
修正后的奇点力学下的库伦定律的另一个方案可表示如下：
[0162]
任意两个点电荷q1、q2由通过连心线方向上的力f
12
相互吸引，该电场力f
12
大小与它们电量的乘积q1q2成正比，与它们之间距离r(数学距离)的平方加上零距离常数xe的平方成反比。即：
[0163][0164]
式中xe是奇点力学下的库伦定律的零距离常数，我们同时规定，两个点电荷q1、q2的体积分别是无穷小，都不能为零。
[0165]
与之对应的，一个电量为q1的点电荷的奇点力学下电场的场强ee为：
[0166][0167]
一个电量为q1的点电荷的在奇点力学下电场的势能ue为：
[0168][0169]
对于一个静止的电量为q1的点电荷，在r＝0处，根据质能关系式，可以得到如下关系：
[0170][0171]
整理可得：
[0172][0173]
或者是：k＝xem
e1
c2/q1。
[0174]
上面的m
e1
是一个静止的电量为q的点电荷的电磁质量，比例系数
[0175]
据此，我们可以将奇点力学下的一个电量为q1的点电荷的奇点力学下电场的场强ee改为以下三种形式：
[0176][0177][0178][0179]
式中的u
e1
＝m
e1
c2。
[0180]
在此需要强调的是，电场中任意两个点电荷之间的距离在奇点力学下就是不再是现有知识中的r。也就是说，即使是r＝0，任意两个质点之间也还是有一个
[0181][0182]
的常数距离。
[0183]
那么，库伦定律中的零距离常数xe的物理意义是什么呢？奇点力学下的任意两个点电荷q1、q2之间的非数学的奇点距离r的物理意义又是什么呢？
[0184]
下面我们直接给出多个具体的应用答案。
[0185]
如上所述，我们定义在奇点力学下，如果点电荷q1、q2是在电场作用下改变运动状态，则该粒子的运动距离可以采用任意两个点电荷q1、q2之间的奇点距离r＝r xe，由此我们得出在奇点力学下的奇点速度概念，即：
[0186]
1、奇点平均速度：在δt时间内，如果两个点电荷q1、q2之间的数学位移为δr,则其奇点位移为r＝δr xe(或者)那么，奇点位移与时刻δt的比值，即为该点电
荷在在δt时间内的奇点平均速度v为：
[0187][0188]
请注意，在δt时间内，当两个点电荷q1、q2之间的数学位移为δr为零时，奇点平均速度v为：
[0189][0190]
在这种情况下，奇点平均速度v就是一种奇点的内在运动。
[0191]
2、奇点瞬时速度：在dt时间内，如果两个点电荷q1、q2之间的数学位移为dr,则其奇点位移为r＝δr xe(或者)那么，对于圆周运动，奇点位移与时刻dt的比值，即为该点电荷在在dt时间内的奇点瞬时速度v为：
[0192][0193]
请注意，当在dt时间内两个点电荷q1、q2之间的数学位移为δr为零时，奇点瞬时速度v为：
[0194][0195]
在这种情况下，奇点瞬时速度v就是一种奇点的内在运动。
[0196]
3、奇点瞬时加速度a：
[0197][0198]
4、对于圆周运动，奇点处的向心加速度a：
[0199][0200]
当r＝0时，
[0201][0202]
5、奇点力学下的牛顿第二运动定律：
[0203][0204]
6、奇点力学下的圆周长l的计算公式：
[0205]
l＝2πr＝2π(r xe)
[0206]
当r＝0时，
[0207]
l＝2πr＝2πxe[0208]
7、奇点力学下的圆面积s的计算公式：
[0209]
s＝πr2＝π(r xe)2[0210]
当r＝0时，
[0211]
s＝πr2＝πx
e2
[0212]
8、奇点力学下的圆体积d的计算公式：
[0213][0214]
当r＝0时，
[0215][0216]
9、奇点力学下的做功的计算公式：
[0217][0218]
如果则
[0219][0220]
10、平行板电容器的真空电容c:
[0221][0222]
式中d为两极板内表面之间的距离。
[0223]
如果实验证明则上面所有的r＝r xe全部替换为
[0224]
下面利用高斯定理来推导奇点力学下的库伦定律。
[0225]
高斯定理(gauss'law)也称为高斯通量理论(gauss'flux theorem)，或称作散度定理、高斯散度定理、高斯－奥斯特罗格拉德斯基公式、奥氏定理或高－奥公式。
[0226]
在静电学中，表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系。高斯定律(gauss'law)表明在闭合曲面内的电荷分布与产生的电场之间的关系。高斯定律在静电场情况下类比于应用在磁场学的安培定律，而二者都被集中在麦克斯韦方程组中。因为数学上的相似性，高斯定律也可以应用于其它由平方反比律决定的物理量，例如引力或者辐照度。
[0227]
奇点力学下的高斯定理指出：穿过一封闭曲面的电通量与奇点力学下的封闭曲面所包围的电荷量成正比，换一种说法：电场强度在一封闭曲面上的面积分与奇点力学下的封闭曲面所包围的电荷量成正比,即：
[0228][0229]
我们定义点电荷q1、q2
…
qi
…
的体积分别是无穷小，都不能为零，在这种情况下，奇点力学下的高斯定理推导出来的一个点电荷电场的公式：
[0230][0231][0232]
奇点力学下该点电荷的电势能u为：
[0233][0234]
上式中电场强度e的物理意义是：当我们用测试电荷测试电场强度时，即使测试电荷与粒子之间的距离r＝0，被测试的点电荷还是存在的，并且这个点电荷还是可以位于一个球面内，在实际中该点电荷体积是非常小，但不能为零，该点电荷的半径是xe，该点电荷的面积是4πxe2，被4πxe2包围在其中的点电荷的电量是q，面积是4πxe2球面上的电通量依然是有限的常量，不能是无穷大。所以，我们用r xe作为积分计算的上限边界，用零作为积分计算的下限边界。也就是说，点电荷与测试电荷之间的距离在奇点力学下就是r xe，不再是现有知识中的r，即使是r＝0，点电荷与测试电荷之间也还是有一个xe的常数距离。
[0235]
如果实验证明则
[0236][0237]
奇点力学下该点电荷的电势能u为：
[0238][0239]
上式中电场强度e的物理意义是：当我们用测试电荷测试电场强度时，即使测试电荷与粒子之间的距离r＝0，被测试的点电荷还是存在的，并且这个点电荷还是可以位于一个球面内，在实际中该点电荷体积是非常小，但不能为零，该点电荷的半径是xe，该点电荷的面积是4πxe2，被4πxe2包围在其中的点电荷的电量是q，面积是4πxe2球面上的电通量依然是有限的常量，不能是无穷大。因此，球面半径r不能为零，而是有一个最小值xe，在球面半径最小值xe之内，球面半径r继续减小后，会导致被包围的电量减少或变得没有，没有电量被包围的球面上的电通量应该为零。所以，我们用r作为积分计算的上限边界，用xe作为积分计算的下限边界。也就是说，点电荷与测试电荷之间的距离在奇点力学下就是不再是现有知识中的r，即使是r＝0，点电荷与测试电荷之间也还是有一个xe的常数距离。
[0240]
上述关于高斯定理的分析计算同样适用于万有引力定律的引力场。
[0241]
为了便于理解库伦定律中零距离常数，我们回顾一下声学基础理论中相关的知识。众所周知，在声学基础理论中，如果势函数以及其他表征介质波动介质波动特性的物理量仅与时间以及空间上称为波心的某一点的距离r有关，这样的纵波称为纵球面波。在各项同性均匀介质中，由点源激起的波就是球面波。所谓点源指的是其线度可以被视为非常小的点状振动体。
[0242]
在奇点力学中，我们用奇点距离r＝r x代替r，故纵球面波的波动方程是：
[0243][0244]
或者是：
[0245][0246]
当距离r＝0时，在奇点力学中纵球面波的波动方程变为：
[0247][0248]
在奇点力学中，式(a)的纵球面波的波动方程的通解形式是：
[0249][0250]
这里的c是纵球面波的波速，f1和f2是任意函数，是发散球面波的势函数，是向中心汇聚的球面波的势函数，x是纵球面波的零距离常数。
[0251]
当距离r＝0时，也就是在点源处，在奇点力学下的纵球面波的波动方程的通解形式是：
[0252][0253]
球面波的波面是一组同心的球面，奇点力学下的发散球面正弦波的方程是：
[0254][0255]
式中k为波矢，α为波源振动的初相位，r为距离波源的距离，a0为在距离r等于1处各个质点振动的振幅，x是发散球面正弦波的零距离常数。
[0256]
在点源处，奇点力学下的发散球面正弦波的方程是：
[0257][0258]
奇点力学下的球面波方程的指数形式是：
[0259][0260]
式中a为复振幅，
[0261]
其中，势函数在包括r＝0处全部满足波动方程：
[0262]
在点源处，奇点力学下的球面波方程的指数形式是：
[0263][0264]
通过以上对声学基础理论中相关知识的介绍，有助于我们理解纵球面波的零距离常数的物理意义，即纵球面波的零距离常数x对应的是在点源处的势函数的状态。显然，任何真实的点源处的势函数不可能是无穷大，这也间接地证明了在库仑定律中，两个点电荷q1、q2之间的距离为零的情况下，两个点电荷q1、q2之间的电场力f
12
不可能是无穷大。
[0265]
如果实验证明则上面所有的r＝r x全部换为
[0266]
下面我们直接给出奇点力学下的薛定谔方程的表达式：
[0267]
[0268]
或者是
[0269][0270]
下面我们直接给出奇点力学下的施瓦西度规(schwarschild metric)的表达式：
[0271][0272]
或者是
[0273][0274]
而奇点力学下的施瓦西度规的解为：
[0275][0276]
或者是
[0277][0278]
上式中的xm为万有引力定律下的零距离常数，g为万有引力常数，m为天体的质量。
[0279]
于是，其中一种奇点力学下的施瓦西解的黑洞视觉半径rs为：
[0280][0281]
如果成立，则有：
[0282][0283]
上述奇点力学下的施瓦西解的黑洞视觉半径rs的数学表达式无疑有助于我们更深刻的理解零距离常数的物理含义。
[0284]
从奇点力学下的施瓦西解的黑洞视觉半径rs的数学表达式可以看出，一个粒子的质量只有在2gm-c2xm≥0的情况下才能成为黑洞，即令其质量满足以下关系：
[0285][0286]
如果不满足这个条件，则rs的数值会是负值。
[0287]
以下是在奇点力学下的广义相对论的钟慢效应的数学表达式：
[0288][0289]
在奇点力学下的广义相对论的钟慢效应的另一种数学表达式：
[0290][0291]
当r＝0时，在奇点力学下的广义相对论的钟慢效应的数学表达式为：
[0292][0293]
如果则当r＝0时，在奇点力学下的广义相对论的钟慢效应的数学表达式为：
[0294][0295]
在奇点力学下的广义相对论的尺缩效应的数学表达式为：
[0296][0297]
也就是
[0298][0299]
或者是
[0300][0301]
也就是
[0302][0303]
当r＝0时，在奇点力学下的广义相对论的尺缩效应的数学表达式为：
[0304][0305]
或者是
[0306][0307]
如果则当r＝0时，在奇点力学下的广义相对论的尺缩效应的数学表达式为：
[0308][0309]
如果实验证明则上面所有的r＝r xm全部换为下面直接给出在引力场中奇点力学下的狭义相对论的尺缩效应的数学表达式：
[0310][0311]
其中的l0为静止参照系中的尺长，即零距离常数xm、也就是是不变的常量，而g为万有引力常数，c为光速。
[0312]
下面直接给出在引力场中奇点力学下的狭义相对论的钟慢效应的数学表达式：
[0313][0314]
其中的δt0为静止参照系中的时间间隔，xm/c为奇点力学下的零时间常数，g为万有引力常数，c为光速。
[0315]
下面直接给出在静电场中奇点力学下的狭义相对论的尺缩效应的数学表达式：
[0316][0317]
其中的l0为静止参照系中的尺长，其中的在静电场中的零距离常数xe为：
[0318][0319]
下面直接给出在静电场中奇点力学下的狭义相对论的钟慢效应的数学表达式：
[0320][0321]
其中的δt0为静止参照系中的时间间隔，xe/c为在静电场中奇点力学下的零时间常数，其中xe为：
[0322][0323]
下面我们直接给出奇点力学下的球极坐标系中的氢原子薛定谔方程的表达式：
[0324][0325]
上式中的xe为库伦定律下的零距离常数。
[0326]
上述奇点力学下的球极坐标系中的氢原子薛定谔方程的表达式同样有助于我们更深刻的理解零距离常数的物理含义。通过求解奇点力学下的球极坐标系中的氢原子薛定
谔方程，也能对库伦定律下的零距离常数xm的具体数值进行理论计算。
[0327]
需要说明的是，奇点力学下的薛定谔方程表达式中，在奇点力学中有一个特殊的解，那就是当r＝0的解。
[0328]
如果实验证明则上面所有的r＝r xe全部替换为
[0329]
当r＝0时，也就是距离粒子的r＝0时，由于粒子自身还有一个零距离常数x的存在，也就是粒子还有一个“残留的”尺寸常数，我们可以用“想象”这个放大镜将粒子所在的位置放大至“无穷大”，这样就有了一个新的空间让我们来分析被放大的粒子了。在这个被“想象”放大产生新的空间中，我们可以建立一个新的三维空间坐标系，这个三维空间坐标系的坐标轴可以用虚数来表示，与之对应的波函数ψ在这个新的三维空间坐标系也是虚数性质的波函数，虚数三维空间坐标系与我们人类熟悉的实数三维空间坐标系空间完全不同，在虚数三维空间坐标系中，物质的形态会发生变化，就是说，实数三维空间坐标系空间中观察看到的具有静止质量的基本粒子，在虚数三维空间坐标系中观察时，会变成没有静止质量、以光速运动的场物质，这个物质形态的变化是我们放大基本粒子所在点至无穷大带来的观察效应。
[0330]
那么，我们在实数三维空间坐标系空间中观察看到的具有静止质量的基本粒子在哪里呢，当然是即在实数三维空间坐标系中，也在虚数三维空间坐标系中，奇点力学下的薛定谔方程表达式中的波函数ψ就是这样的一个函数。
[0331]
波函数ψ就是在实数三维空间坐标系中存在、同时也在虚数三维空间坐标系中存在的函数。
[0332]
在实数三维空间坐标系中的基本粒子的波函数ψ在实数三维空间坐标系中表达出的是粒子性，在实数三维空间坐标系中的基本粒子的波函数ψ在虚数三维空间坐标系中表达出的是波动性。
[0333]
如果我们是对虚数三维空间坐标系中的基本粒子进行放大至无穷大的空间变化处理，这样还会出现一个新的空间让我们来分析虚数三维空间坐标系中被放大的粒子。在这个被“想象”放大产生新的空间中，我们还是可以建立一个新的三维空间坐标系，这个三维空间坐标系的坐标轴可以用超虚数来表示，与之对应的波函数ψ在这个新的三维空间坐标系也是超虚数性质的波函数，超虚数三维空间坐标系与我们人类熟悉的实数三维空间坐标系空间更是完全不同，在超虚数三维空间坐标系中，物质的形态会继续发生变化。
[0334]
如上所述，在实数三维空间坐标系空间中观察看到的具有静止质量的基本粒子，在虚数三维空间坐标系中观察时，会变成没有静止质量、以光速运动的场物质，这个物质形态的变化是我们放大基本粒子所在点至无穷大带来的观察效应。
[0335]
而在虚数三维空间坐标系空间中观察看到的具有静止质量的基本粒子，在实数三维空间坐标系中观察时，会变成虚粒子，也就是根本观测不到。这个物质形态的变化是虚数三维空间坐标系的性质带来的观察效应。但是，在超虚数三维空间坐标系中去观察在虚数三维空间坐标系空间中具有静止质量的基本粒子，该基本粒子会变成没有静止质量、以光速运动的场物质，这个物质形态的变化同样是我们放大该基本粒子所在点至无穷大带来的观察效应。
[0336]
我们同样可以用“想象”缩小镜将我们所在的这个宇宙空间缩小至“无穷小”，这样同样会出现一个新的空间，假设我们进入这个新的三维空间，并在这个被“想象”缩小产生
新的空间中立一个新的三维空间坐标系，这个三维空间坐标系的坐标轴可以用超实数来表示，与之对应的波函数ψ在这个新的三维空间坐标系也是超实数性质的波函数，超实数三维空间坐标系与我们人类熟悉的实数三维空间坐标系空间完全不同，在超实数三维空间坐标系中，物质的形态也会发生变化，就是说，实数三维空间坐标系空间中观察看到的具有静止质量的基本粒子，在超实数三维空间坐标系中观察时，会类似虚粒子，也就是根本观测不到。这个物质形态的变化是超实数三维空间坐标系的性质带来的观察效应。而在超实数三维空间坐标系中去观察在实数三维空间坐标系空间中以光速运动的场物质时，会发现这些场物质是具有静止质量的基本粒子，这个物质形态的变化同样是我们缩小该我们宇宙至无穷小带来的观察效应。
[0337]
需要指出的是，超实数三维空间坐标系也可以通过“想象”缩小镜将其缩小至“无穷小”，随之而产生的则是超超实数三维空间坐标系，如此循环向上，可以有无限多个新的实数三维空间坐标系。而超虚数三维空间坐标系也可以通过“想象”放大镜将其内部的一个点放大至“无穷大”，随之而产生的则是超超虚数三维空间坐标系，如此循环向下，可以有无限多个新的虚数三维空间坐标系。而一个真实的在某一空间坐标系中的“粒子”，可以在所有的三维空间坐标系中都存在，只不过其存在的形态是变化的，在不同性质的三维空间坐标系，该粒子具有不同性质的物质形态。
[0338]
那么，我们在实数三维空间坐标系空间中观察看到的具有静止质量的基本粒子在哪里呢，当然是即在超实数三维空间坐标系中，也在虚数三维空间坐标系中，奇点力学下的薛定谔方程表达式中的波函数ψ同样就是这样的一个函数。
[0339]
波函数ψ就是在超实数三维空间坐标系中存在、同时也在虚数三维空间坐标系中存在的函数。
[0340]
如果超实数三维空间坐标系中的基本粒子的波函数ψ在超实数三维空间坐标系中表达出的是粒子性，在超实数三维空间坐标系中的基本粒子的波函数ψ在实数三维空间坐标系中表达出的就是波动性。
[0341]
众所周知，为了描述一个物体的运动，通常是选择另一个物体作为参照物，为了方便地描述物体之间的相对运动规律，我们应尽可能的选择与被描述物体存在相互作用或相对运动的物体作为参照系。我们规定与被描述物体之间存在相互作用或相对运动的、被选作参考的物体为相对参照系，被选作参考的物体的运动状态可以是任意的。
[0342]
用相对参照系描述物体之间的相对运动时，可以得到如下规律：
[0343][0344]
式中m1和m2分别为相互作用的二个物体的质量，f
12
为相互作用的二个物体之间的相互作用力，a
12
为相互作用的二个物体之间相对运动所具有的的加速度，f1是质量为m1的物体所受的外力作用，f2是质量为m2的物体所受的外力作用。以上数学表达式所表达的运动规律我们称之为相对运动定律。
[0345]
下面我们用相对运动定律来分析一个黑洞与另一个物体相互作用的运动规律。
[0346]
设黑洞1的质量为m1，物体2的质量为m2，假设二者之间只有彼此的万有引力作用，忽略其他的外力作用，由奇点力学下的万有引力定律：
[0347][0348]
以及相对运动定律，可得到：
[0349][0350]
整理得到二者之间相对运动的加速度为：
[0351][0352]
设物体2在距离黑洞原点的奇点距离r处，也就是距离黑洞r xm处，物体2的重力势能
[0353]
物体2要想与黑洞1脱离，其相对运动速度v所具有的相对能量要大于重力势能取二者正好相等为临界值，可以得到：
[0354][0355]
将相关的已知数据代入上式，并解这个方程式，就可以得到物体2在距离黑洞原点的奇点距离r xm处的脱离速度v与距离黑洞原点的奇点距离r xm之间在临界值下的关系了，这个关系能帮助我们定性地了解万有引力定律中的零距离常数xm的物理意义。
[0356]
如果实验证明则上面所有的r＝r xe全部替换为
[0357]
实验发现，电子具有自旋运动,根据奇点力学，电子具有的自旋运动可以用奇点力学下的周长计算公式加以计算分析，即电子具有的自旋运动是在r＝0状态下、电子自身的旋转运动，根据奇点力学下的面积计算公式，电子的自旋面积s为：
[0358][0359]
在奇点力学下，电子自旋的周长l为：
[0360][0361]
再设定电子是一个稳定的圆环形驻波，即电子在虚数三维空间坐标系是在做自旋的环绕运动，自旋的周长为其波长λ，于是，得到电子自旋的半径xb为：
[0362][0363]
而电子自旋的电流强度i＝-νe，由此，我们可以计算出电子自旋的磁矩μs:
[0364][0365]
在上面的计算中电子自旋的半径xb为：
[0366][0367]
有可能就是与毕奥-萨伐尔定律中零距离常数相关的数值，可以作为分析本发明的实验数据时的参考。
[0368]
本发明的利用变距实验测量毕奥-萨伐尔定律中零距离常数的方法，其包括如下步骤：
[0369]
a、设置一个直的长度为dl的长导线，给长导线通上电流强度为i的恒稳电流；
[0370]
b、利用可测量磁感应强度的装置，在长导线附近的空间点p1处测量该处的磁感应强度，得到该处磁感应强度参数b1，利用测距装置测量空间点p1与长导线的中心线之间的距离r1，得到距离参数r1，利用角度测量装置，测量空间点p1与长导线二端连线之间的夹角θ1；
[0371]
c、沿着长导线的垂直方向移动测量磁感应强度的装置，在长导线附近的空间点p2处测量该处的磁感应强度，得到该处磁感应强度参数b2，利用测距装置测量空间点p2与长导线的中心线之间的距离，得到距离参数r2，利用角度测量装置，测量空间点p2与长导线二端连线之间的夹角θ2，所述距离r2为距离r1的2倍以上；
[0372]
d，重复步骤c多次，即利用可测量磁感应强度的装置，在长导线附近的空间点p3、p4、
……
处分别测量该处的磁感应强度，分别得到对应的磁感应强度参数b3、b4、
……
，利用测距装置分别测量空间点p3、p4、
……
与长导线的中心线之间的距离，得到多个距离参数r3、r4、
……
，利用角度测量装置，分别测量空间点p3、p4、p5、
……
与长导线二端连线之间的夹角θ3、θ4、
……
；
[0373]
所述距离r3为距离r2的2倍以上，距离ri为距离ri-1的2倍以上，距离r4为距离r3的2倍以上，
……
；
[0374]
e、根据修正后的毕奥-萨伐尔定律公式：
[0375][0376]
式中xb是毕奥-萨伐尔定律的距离修正常数；
[0377]
将多次测量得到的数据分别代入修正后的毕奥-萨伐尔定律公式，分别得到：
[0378][0379][0380][0381][0382]
……
[0383]
将上面的4个代入了测量得到的数据的修正后的毕奥-萨伐尔定律公式分别相互进行相除处理，可得到：
[0384]
b1/b2＝[sinθ1/(r1 x)2]/[sinθ2/(r2 xb)2]
ꢀꢀꢀ
(1)
[0385]
b1/b3＝[sinθ1/(r1 x)2]/[sinθ3/(r3 xb)2]
ꢀꢀꢀ
(2)
[0386]
b1/b4＝[sinθ1/(r1 x)2]/[sinθ4/(r4 xb)2]
ꢀꢀꢀ
(3)
[0387]
b2/b3＝[sinθ2/(r2 x)2]/[sinθ3/(r3 xb)2]
ꢀꢀꢀ
(4)
[0388]
b2/b4＝[sinθ2/(r2 x)2]/[sinθ4/(r4 xb)2]
ꢀꢀꢀ
(5)
[0389]
b3/b4＝[sinθ3/(r3 x)2]/[sinθ4/(r4 xb)2]
ꢀꢀꢀ
(6)
[0390]
……
[0391]
根据实验测量到的b1、b2、b3、b4、
……
、θ1、θ2、θ3、θ4、
……
、和r1、r2、r3、r4、
……
计算后，即可得出毕奥-萨伐尔定律中多个距离修正常数xb的具体数值,如果所得到的多个距离修正常数xb不一致，也就是距离修正常数xb是变化不定的变数，这表明修正后的(1)式的修正后的毕奥-萨伐尔定律公式有偏差，则将修正后的毕奥-萨伐尔定律的公式调整为：
[0392][0393]
然后重新利用步骤e进行计算处理，直至根据计算多个实验数据所得到的xb接近于一个常数或者就是一个常数，则该常数xb即为修正后的毕奥-萨伐尔定律中零距离常数xb的具体数值，而与之对应的公式，即为修正后的修正后的毕奥-萨伐尔定律。
[0394]
作为本发明的进一步改进，上述步骤c中，改变二个物体之间的距离时，让距离ri为距离ri-1的3—20倍。
[0395]
作为本发明的进一步改进，上述步骤c中，改变二个物体之间的距离时，让距离ri为距离ri-1的5—15倍。
[0396]
作为本发明的进一步改进，上述步骤c中，改变二个物体之间的距离时，让距离ri为距离ri-1的8—12倍。
[0397]
作为本发明的进一步改进，上述可测量磁感应强度的装置为便携式磁场测试仪。
[0398]
作为本发明的进一步改进，上述长导线中的电流强度i大于20安培，所述重复步骤c的次数大于30次。
[0399]
在本发明的步骤中，都特别提到要拉开距离，这是为了能够更精确的测量出的毕奥-萨伐尔定律中零距离常数xb，而太小范围的距离变化，会让实验数据的精度不够，不利于得出的毕奥-萨伐尔定律中零距离常数xb的精确数值。