2-DOF直升机系统自适应神经网络量化容错控制方法

2-dof直升机系统自适应神经网络量化容错控制方法
技术领域
1.本发明涉及直升机系统控制技术领域，具体地说，涉及一种2-dof直升机系统自适应神经网络量化容错控制方法。


背景技术：

2.与固定翼无人机相比，无人直升机可进行特殊的操作，如横向飞行，垂直起飞或悬停等。无人直升机的优点引起越来越多研究人员的关注，并已在许多领域得到了成功应用。但无人直升机的动力学模型非常复杂，且具有非线性、强耦合性和系统不稳定性等特点。此外，在飞行过程中还会受到来自非光滑执行器输入约束的影响，这都为其控制器的分析和设计增加了难度。
3.为了能稳定的控制直升机系统，科研人员提出了许多控制方法，其中就包括将直升机的非线性模型线性化以后再进行控制，还有直接对系统参数是已知的非线性模型设计控制器。但是，这些方法都只在最理想情况下考虑直升机飞行控制器的设计，在实际情况中，直升机系统是一个未知不确定的非线性系统，上述的这些方法都不再适用。此外，直升机在实际情况中，会不可避免的受到执行器故障和未知死区的影响，同时，其内部信号的传输也会因为通信压力过大导致信号的抖颤，这些因素的影响都会使得直升机系统的不稳定。


技术实现要素：

4.本发明的内容是提供一种2-dof直升机系统自适应神经网络量化容错控制方法，其能够克服现有技术的某种或某些缺陷。
5.根据本发明的2-dof直升机系统自适应神经网络量化容错控制方法，其包括以下步骤：
6.步骤1：建立2-dof直升机系统的动力学模型；
7.步骤2：利用磁滞量化器来减少量化信号中的颤振；设计辅助系统，以补偿未知的死区和执行器故障的影响；采用径向基函数神经网络对系统进行近似；并构建系统方程；
8.步骤3：构建李雅普诺夫方程；
9.步骤4：根据李雅普诺夫方程，构建系统的控制器和自适应律；
10.步骤5：根据李雅普诺夫方程、系统控制器和自适应律，证明2-dof直升机系统的稳定性；
11.步骤6：进行仿真，整理结果。
12.作为优选，步骤1中，根据拉格朗日力学模型，系统的非线性动力学方程如下：
13.[0014][0015]
其中，j
p
和jy分别表示为围绕俯仰轴和偏航轴的惯性矩，v
p
和vy表示两个电机的输入电压，m表示直升机的质量，la表示距离机身固定框架原点的质心距离，θ表示俯仰角，φ表示偏航角，k
pp
表示俯仰螺旋桨中作用于俯仰轴上的扭矩推力增益，k
py
表示偏航螺旋桨中作用于俯仰轴上的扭矩推力增益，k
yy
表示偏航螺旋桨中作用于偏航轴上的扭矩推力增益，k
yp
表示俯仰螺旋桨中作用于偏航轴上的扭矩推力增益，d
p
和dy表示黏性摩擦系数；
[0016]
定义q＝[q1,q2]
t
，q1＝[θ,φ]
t
和考虑到系统中的不确定性，非线性2-dof直升机系统模型为：
[0017][0018][0019]
y＝q1(5)
[0020]
其中，q,q1,q2分别是系统变量，输出角度变量和角速度变量，δa(q)、δb(q)表示系统得到不确定项，分别表示角度变量的导数和角速度变量的导数，u＝[v
p
,vy]
t
表示系统的控制输入；a(q)和b(q)是系统的增益矩阵，分别为：
[0021][0022][0023]
g表示重力加速度。
[0024]
作为优选，步骤2中，执行器故障包括增益故障和偏置故障，统一描述如下：
[0025][0026]
其中，uf(t)表示执行器故障输入，表示有效因子，ζ(t)表示未知有界信号；
[0027]
死区表达式如下所示：
[0028][0029]
其中，u(t)表示死区的输出，d()表示死区符号，v(t)表示死区的输入，ψ＞0、b
l
＞0、br＞0都表示死区的未知参数；
[0030]
将死区方程(9)改写为：
[0031]
d(v(t))＝ψv(t) χ(v(t))
ꢀꢀꢀ
(10)
[0032]
其中，
[0033][0034]
χ表示死区项，死区参数ψ是有界的，因此，调用(9)，有：
[0035]
|χ(v(t))|≤χ*
ꢀꢀꢀ
(11)
[0036]
其中，χ*＝max{ψb
l
,-ψbr}；
[0037]
为了减轻通信负担，需要将信号量化，为了避免信号量化过程中出现抖动，引入滞后量化器，因此，对死区的输入可以表示为：
[0038]
v(t)＝q(τ)
[0039]
其中，v(t)是死区的输入，q(τ)表示磁滞量化器，τ表示需要被量化的信号；
[0040]
然后，将量化定义为：
[0041][0042]
其中，τi＝ρ
1-i
τ
min
,(i＝1,2,
…
),τ
min
＞0，0＜ρ＜1表示量化密度；q(τ)∈u＝{0,
±
τi,
±
τi(1 δ),i＝1,2,
…
}，τ
min
表示量化的死区大小；q(τ(t-))表示q(τ)之前的时刻状态；
[0043]
此外，磁滞量化器还可以表示为：
[0044]
q(τ)＝g(τ)τ(t) t(t)
ꢀꢀꢀ
(12)
[0045]
其中，1-δ＜g(τ)＜1 δ和|t(t)|≤τ
min
都是增益函数，g(τ)表示一个未知的增益，τ(t)表示需要被量化的信号，δ表示一个量化参数；
[0046]
考虑(8)，(10)和(12)，重新改写为：
[0047][0048]
定义定义是一个未知的正整数，因为ψ都是未知正整数，有：
[0049][0050]
其中，a(q)，b(q)表示系统的增益矩阵，δa(q)，δb(q)表示系统中的不确定项，是一个未知的正整数，表示有效因子，ζ(t)表示未知有界信号，t增益函数，ψ表示死区参数，χ表示死区项；
[0051]
由于增益矩阵b的逆矩阵会不存在，引入τ＝b
t
(q)v，其中v是一个预期的控制信号；然后，得到系统方程如下所示：
[0052][0053]
其中，γ是一个设计参数；
[0054]
表示一个未知方程，也表示一个未知方程；
[0055]
因为ζ(t)表示未知有界信号，且|χ(v(t))|≤χ*，得出|ξ|≤ξf，其中，ξf表示未知正整数；
[0056]
此外，引入一个径向基函数神经网络来估计系统中的q(q,v)，因此，得出下式：
[0057]
q(q,ν)＝ψ
*t
d(x) ∈(x)
[0058]
其中，ψ
*t
表示神经网络的理想权重的转秩，d(x)表示神经元激活函数，∈(x)表示神经网络的近似误差，且存在一个未知的正常数∈
*
，使得‖∈‖≤∈
*
。
[0059]
作为优选，步骤3中，根据步骤1中给出的内容，构建李雅普诺夫函数方程：
[0060][0061][0062][0063]
其中，表示一个未知正整数，径向基神经网络的权重误差，和表示常数误差，z1＝q
1-qd表示角度跟踪误差，q1表示系统输出的角度变量，qd表示期望轨迹，z2＝q
2-α表示跟踪误差的导数，q2表示系统输出的角速度变量，α表示虚拟控制器，λ1和λ2表示设计参数；v1、v2、v3都表示李雅普诺夫方程。
[0064]
作为优选，步骤4中，虚拟控制器为：
[0065][0066]
其中，k1表示增益对角矩阵，z1表示角度误差，表示期望轨迹的导数；
[0067]
控制器为：
[0068]
[0069][0070]
其中，v是期望控制器，和表示常数的估计值，a(q)，b(q)表示系统的增益矩阵，表示径向基函数神经网络的估计权重值的转秩，γ表示一个设计参数，δ表示量化参数，表示一个双曲正切函数，d1表示一个很小的正整数。
[0071]
自适应律为：
[0072][0073][0074][0075]
其中，表示神经网络的自适应律，和表示常数的自适应律；γ表示一个对角矩阵，λ1、λ2、σ1、σ2、σ3表示系统中的设计参数，均为正数；表示径向基神经网络估计的权重，d(x)表示表示神经元激活函数，表示角速度误差的转秩。
[0076]
作为优选，步骤5中，首先对v2进行求导：
[0077][0078]
再对v3求导，可得：
[0079][0080]
再将(17)代入上式中，得：
[0081][0082]
推导出以下不等式：
[0083][0084]
再根据杨氏不等式，得出：
[0085][0086]
其中，ξ1和ξ2都是常数，||ψ
*
||表示径向基函数神经网络的范数；
[0087]
将(19)和(20)代入(18)中，可以得出：
[0088][0089]
其中，
[0090][0091]
此外，得出下列不等式：
[0092][0093][0094]
当上面的不等式满足条件时，证得v3是半全局稳定的。
[0095]
本发明考虑了执行器故障和未知死区2-dof直升机系统的综合效应，为了消除执行器故障和未知死区耦合引起的非线性，设计了一个辅助系统来处理耦合效应。此外，还引入的磁滞量化器减轻了量化信号的抖动。同时，综合考虑了量化信号、执行器故障和未知死区的耦合效应，设计了一种合理的控制器。该控制方法考虑了实际的2-dof直升机系统中的不确定性、未知死区和执行器故障，可以将其应用到实际的直升机系统中，具有一定的实用价值。
附图说明
[0096]
图1为实施例1中一种2-dof直升机系统自适应神经网络量化容错控制方法的流程
图；
[0097]
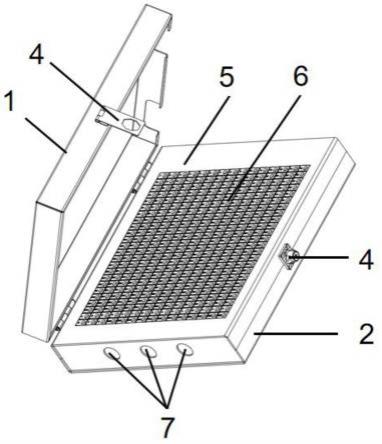
图2为实施例1中2-dof直升机的模型简图。
[0098]
图3：2-dof直升机俯仰角的角度跟踪期望角度的轨迹图；
[0099]
图4：2-dof直升机偏航角的角度跟踪期望角度的轨迹图；
[0100]
图5：2-dof直升机俯仰角的角速度跟踪期望角度的轨迹图；
[0101]
图6：2-dof直升机偏航角的角速度跟踪期望角度的轨迹图；
[0102]
图7：2-dof直升机角度误差轨迹跟踪响应图；
[0103]
图8：2-dof直升机系统的控制输入。
具体实施方式
[0104]
为进一步了解本发明的内容，结合附图和实施例对本发明作详细描述。应当理解的是，实施例仅仅是对本发明进行解释而并非限定。
[0105]
实施例1
[0106]
如图1所示，本实施例提供了一种2-dof直升机系统自适应神经网络量化容错控制方法，其包括以下步骤：
[0107]
步骤1：建立2-dof直升机系统的动力学模型；
[0108]
步骤1中，根据拉格朗日力学模型，系统的非线性动力学方程如下：
[0109][0110][0111]
其中，j
p
和jy分别表示为围绕俯仰轴和偏航轴的惯性矩，v
p
和vy表示两个电机的输入电压，m表示直升机的质量，la表示距离机身固定框架原点的质心距离，θ表示俯仰角，φ表示偏航角，k
pp
表示俯仰螺旋桨中作用于俯仰轴上的扭矩推力增益，k
yp
表示偏航螺旋桨中作用于俯仰轴上的扭矩推力增益，k
yy
表示偏航螺旋桨中作用于偏航轴上的扭矩推力增益，k
yp
表示俯仰螺旋桨中作用于偏航轴上的扭矩推力增益，d
p
和dy表示黏性摩擦系数；
[0112]
定义q＝[q1,q2]
t
，q1＝[θ,φ]
t
和考虑到系统中的不确定性，非线性2-dof直升机系统模型为：
[0113][0114][0115]
y＝q1ꢀꢀꢀ
(5)
[0116]
其中，q,q1,q2分别是系统变量，输出角度变量和角速度变量，δa(q)、δb(q)表示系统得到不确定项，分别表示角度变量的导数和角速度变量的导数，u＝[v
p
,vy]
t
表示系统的控制输入；a(q)和b(q)是系统的增益矩阵，分别为：
[0117][0118][0119]
g表示重力加速度。
[0120]
步骤2：利用磁滞量化器来减少量化信号中的颤振；设计辅助系统，以补偿未知的死区和执行器故障的影响；采用径向基函数神经网络对系统进行近似；并构建系统方程；
[0121]
步骤2中，执行器故障包括增益故障和偏置故障，统一描述如下：
[0122][0123]
其中，uf(t)表示执行器故障输入，表示有效因子，ζ(t)表示未知有界信号；
[0124]
死区表达式如下所示：
[0125][0126]
其中，u(t)表示死区的输出，d()表示死区符号，v(t)表示死区的输入，ψ＞0、b
l
＞0、br＞0都表示死区的未知参数；
[0127]
将死区方程(9)改写为：
[0128]
d(v(t))＝ψv(t) χ(v(t))
ꢀꢀꢀ
(10)
[0129]
其中，
[0130][0131]
χ表示死区项，死区参数ψ是有界的，因此，调用(9)，有：
[0132]
|χ(v(t))|≤χ*
ꢀꢀꢀ
(11)
[0133]
其中，χ*＝max{ψb
l
,-ψbr}；
[0134]
为了减轻通信负担，需要将信号量化，为了避免信号量化过程中出现抖动，引入滞后量化器，因此，对死区的输入可以表示为：
[0135]
v(t)＝q(τ)
[0136]
其中，v(t)是死区的输入，q(τ)表示磁滞量化器，τ表示需要被量化的信号；
[0137]
然后，将量化定义为：
[0138][0139]
其中，τi＝ρ
1-i
τ
min
,(i＝1,2,
…
),τ
min
＞0，0＜ρ＜1表示量化密度；q(τ)∈u＝{0,
±
τi,
±
τi(1 δ),i＝1,2,
…
}，τ
min
表示量化的死区大小；q(τ(t-))表示q(τ)之前的时刻状态；
[0140]
此外，磁滞量化器还可以表示为：
[0141]
q(τ)＝g(τ)τ(t) t(t)
ꢀꢀꢀ
(12)
[0142]
其中，1-δ＜g(τ)＜1 δ和|t(t)|≤τ
min
都是增益函数，g(τ)表示一个未知的增益，τ(t)表示需要被量化的信号，δ表示一个量化参数；
[0143]
考虑(8)，(10)和(12)，重新改写为：
[0144][0145]
定义定义是一个未知的正整数，因为ψ都是未知正整数，有：
[0146][0147]
其中，a(q)，b(q)表示系统的增益矩阵，δa(q)，δb(q)表示系统中的不确定项，是一个未知的正整数，表示有效因子，ζ(t)表示未知有界信号，t增益函数，ψ表示死区参数，χ表示死区项；
[0148]
由于增益矩阵b的逆矩阵会不存在，引入τ＝b
t
(q)v，其中v是一个预期的控制信号；然后，得到系统方程如下所示：
[0149][0150]
其中，γ是一个设计参数；
[0151]
表示一个未知方程，
也表示一个未知方程；
[0152]
因为ζ(t)表示未知有界信号，且|χ(v(t))|≤χ*，得出|ξ|≤ξf，其中，ξf表示未知正整数；
[0153]
此外，引入一个径向基函数神经网络来估计系统中的q(q,v)，因此，得出下式：
[0154]
q(q,ν)＝ψ
*t
d(x) ∈(x)
[0155]
其中，ψ
*t
表示神经网络的理想权重的转秩，d(x)表示神经元激活函数，∈(x)表示神经网络的近似误差，且存在一个未知的正常数∈
*
，使得‖∈‖≤∈
*
。
[0156]
步骤3：构建李雅普诺夫方程；
[0157]
步骤3中，根据步骤1中给出的内容，构建李雅普诺夫函数方程：
[0158][0159][0160][0161]
其中，表示一个未知正整数，径向基神经网络的权重误差，和表示常数误差，z1＝q
1-qd表示角度跟踪误差，q1表示系统输出的角度变量，qd表示期望轨迹，z2＝q
2-α表示跟踪误差的导数，q2表示系统输出的角速度变量，α表示虚拟控制器，λ1和λ2表示设计参数；v1、v2、v3都表示李雅普诺夫方程。
[0162]
步骤4：根据李雅普诺夫方程，构建系统的控制器和自适应律；
[0163]
步骤4中，虚拟控制器为：
[0164][0165]
其中，k1表示增益对角矩阵，z1表示角度误差，表示期望轨迹的导数；
[0166]
控制器为：
[0167][0168][0169]
其中，v是期望控制器，和表示常数的估计值，a(q)，b(q)表示系统的增益矩阵，表示径向基函数神经网络的估计权重值的转秩，γ表示一个设计参数，δ表示量化参数，表示一个双曲正切函数，d1表示一个很小的正整数。
[0170]
自适应律为：
[0171][0172][0173][0174]
其中，表示神经网络的自适应律，和表示常数的自适应律；γ表示一个对角矩阵，λ1、λ2、σ1、σ2、σ3表示系统中的设计参数，均为正数；表示径向基神经网络估计的权重，d(x)表示表示神经元激活函数，表示角速度误差的转秩。
[0175]
步骤5：根据李雅普诺夫方程、系统控制器和自适应律，证明2-dof直升机系统的稳定性；
[0176]
步骤5中，首先对v2进行求导：
[0177][0178]
再对v3求导，可得：
[0179][0180]
再将(17)代入上式中，得：
[0181][0182]
推导出以下不等式：
[0183][0184]
再根据杨氏不等式，得出：
[0185][0186]
其中，ξ1和ξ2都是常数，||ψ
*
||表示径向基函数神经网络的范数；
[0187]
将(19)和(20)代入(18)中，可以得出：
[0188][0189]
其中，
[0190][0191]
此外，得出下列不等式：
[0192][0193][0194]
当上面的不等式满足条件时，证得v3是半全局稳定的。
[0195]
步骤6：进行仿真，整理结果。
[0196]
本实施例公开了一种针对具有未知死区和执行器故障的2-dof直升机系统的自适应神经量化容错控制方法。该方法实现了所需设定点和轨迹的渐近姿态调整和跟踪。首先，利用磁滞量化器来减少量化信号中的颤振。为了解决非线性直升机系统中的不确定性，采用径向基函数神经网络对其进行近似。此外，还设计了一个辅助系统，以补偿未知的死区和执行器故障的影响。在神经网络和辅助系统的基础上，针对非线性2-dof直升机系统设计了一种自适应神经网络量化容错控制策略。然后，通过严格的李亚普诺夫稳定性分析，证明了封闭环系统的信号是半全局均匀的和有界的。最后，再matlab仿真软件上证明了该控制策略的有效性和合理性。
[0197]
图2为2-dof直升机的模型简图，其中，yaw是俯仰角，pitch是偏航角，x，y，z分别是x轴，y轴和z轴，f
p
是前电机产生的推力，fy是后电机产生的推力。front和back分别表示前电机和后电机。图3和图4分别是在控制直升机运动过程中的俯仰和偏航角跟踪期望轨迹的示
意图。图5和图6分别是在控制直升机过程中俯仰和偏航角的角速度与期望轨迹的示意图，从图中也可以看出角速度也能完全跟踪到期望轨迹。图7表示俯仰和偏航角在跟踪期望轨迹的过程中所产生的跟踪误差。图8表示控制系统的输入。从上述仿真结果可知本发明所提出的控制方法在控制2-dof直升机系统中具有一定的优越性。
[0198]
以上示意性的对本发明及其实施方式进行了描述，该描述没有限制性，附图中所示的也只是本发明的实施方式之一，实际的结构并不局限于此。所以，如果本领域的普通技术人员受其启示，在不脱离本发明创造宗旨的情况下，不经创造性的设计出与该技术方案相似的结构方式及实施例，均应属于本发明的保护范围。