配电信息物理系统可靠性评估方法与流程

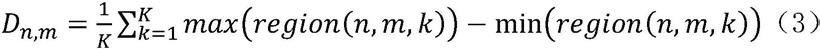
1.本发明属于配电网技术领域，尤其涉及配电网通信系统故障下的配电网可靠性评估。


背景技术：

2.地球温室效应和生态环境的不断恶化以及厄尔尼诺的出现，导致台风等极端自然灾害呈现越来越高发的态势。极端自然灾害造成了电网设施发生大规模故障，其导致的巨额的停电经济损失使电网的灾害应对能力得到了广泛关注。配电线路与用户负荷密切相关，是电网的重要组成部分，保证配电线路的安全可靠是整个电力系统稳定、经济运行的集中体现。但同时配电线路灾害应对能力较弱，而且不同地方配电网的设备质量参差不齐，故有必要对配电网进行灾害应对能力评估技术研究也即可靠性评估。
3.可靠性评估方法一般分为两种，模拟法和解析法。模拟法是基于蒙特卡洛模拟法对可靠性评估涉及的随机变量都采用抽样技术求取可靠性指标的一种评估方法，速度慢、计算时间长、收敛性能差；解析法枚举电网每一种故障，得出每种情况发生的概率以及造成的后果，从而计算出电网的可靠性指标，具有物理概念清晰，计算速度快，结果精确的优点。传统配电网可靠性评估假设通信系统完全可靠，而事实情况是通信系统的可靠性对配电网的可靠性会造成影响。假设配电网通信系统完全可靠势必造成系统可靠性指标评估较为乐观。
4.目前，国内外研究了配电信息物理系统(cpds)的可靠性评估。具有代表性的有：1)将配电网的信息系统的可靠性分为拓扑可靠性，时延可靠性和误码可靠性，结合蒙特卡洛模拟法评估cpds的可靠性。2)利用频域-时域变换评估信息系统可靠性，并利用等效法与最小路径法结合的方法对配电网的物理系统进行建模。当前评估方法都利用蒙特卡洛模拟法，求解速度慢，收敛性能差，难以快速找出配电网的薄弱环节并进行有针对性的补救措施。因此，需要一种配电信息物理系统可靠性评估方法。


技术实现要素：

5.本发明的目的在于提供一种配电信息物理系统可靠性评估方法，从而克服了现有配电网的物流系统通过蒙特卡洛法评估仿真求解时间长、收敛速度慢的缺点。
6.为实现上述目的，本发明提供了一种配电信息物理系统可靠性评估方法，包括以下步骤：
7.根据配电网原始数据建立配电网信息物理系统的可靠性评估模型；
8.对所述可靠性评估模型分成多个子单元，分别计算每一个单元的状态占用概率向量；
9.根据所述概率向量构建配电网信息物理系统的状态转移概率矩阵；
10.根据所述状态概率转移矩阵计算各个子单元故障状态下的后果；
11.根据所述后果计算电网信息物理系统的可靠性指标。
12.优选地，所述可靠性评估模型分为：物理层、网络层以及决策层三个单元。
13.优选地，所述配电网原始数据包括：配电网物理子系统和信息子系统的拓扑图以及配电网组成元件的故障率、修复时间。
14.优选地，各个子单元故障状态下的后果包括停电时间和停电次数。
15.优选地，建立配电网信息物理系统的可靠性评估模型分为元件建模和网络链路建模。
16.优选地，所述网络链路建模包括：
17.通过分析可靠性评估模型中的网络的拓扑结构，形成可达矩阵，分析主站到各个ied的连通性，确定信道；
18.分别判断信道的延时可靠性，选择延时可靠性最高的一条信道作为最优信道；
19.对所述最优信道进行误码可靠性的评估，从而完成对网络链路模型的建模和评估。
20.优选地，根据所述状态概率转移矩阵计算各个子单元故障状态下的后果，具体包括：
21.按照配电网故障处理的过程，根据各最小隔离区与电源的连接关系将各最小隔离区分为四种情况；
22.当网络子系统发生故障时，故障引发的后果根据四种所述情况进行停电时间和停电次数的计算，并重新划分受影响的区域，重新划分区域后再根据四种所述情况计算停电时间和停电次数。
23.优选地，根据各最小隔离区与电源的连接关系将各最小隔离区分为四种情况，具体包括：
24.故障发生后，不受故障影响而与主电源保持连接的区域记为a类区域，所述a类区域内负荷的停运时间等于0；
25.故障发生后与主电源失去连接，然后在操作隔离开关隔离故障区域之后恢复与主电源之间连接的区域记为b类区域，所述b类区域内负荷的停运时间等于隔离开关的操作时间；
26.故障发生后与主电源失去连接，然后在故障隔离之后，通过联络开关与备用电源连接而恢复通电的区域记为c类区域，所述c类区域内负荷的停运时间等于联络开关操作时间；
27.直到故障排除后，才恢复供电的区域记为d类区域，所述d类区域内负荷的停运时间等于故障的修复时间。
28.优选地，其特征在于，重新划分受影响的区域包括以下步骤：
29.若网络故障导致故障与电源最小路上离故障最近的开关动作发生故障，则在所述最小路上的上游寻找最近的能动作的隔离开关；其中，所述电源最小路为故障与电源的最短路径。
30.若网络故障导致故障与联络开关最小路上离故障最近的开关动作发生故障，则在此最小路上往下游寻找最近的能动作的隔离开关即可；其中，所述联络开关最小路为故障与联络开关的最短路径。
31.优选地，所述可靠性指标包括：配电网平均停电频率指标、配电网平均停电持续时
间指标、平均供电可用率指标以及户平均停电持续时间指标。
32.与现有的技术相比，本发明具有如下有益效果：
33.1、本发明所提供的配电信息物理系统cpds可靠性评估方法，通过将配电信息物理系统cpds拆分为三个互斥的子系统，分别计算各个子系统处于不同运行状态的概率，从而得到整个配电网信息物理系统在不同运行状态的概率。系统的每一种运行状态对应一种后果(停电次数与停电时间)，通过计算这些后果从而得出配电信息物理系统的可靠性指标。该配电信息物理系统可靠性评估方法物理意义明确、运算以及收敛速度快，克服了蒙特卡洛法仿真求解时间长、收敛速度慢的不足。
34.2、本发明中，对所述可靠性评估模型分成多个子单元，分别计算每一个单元的状态占用概率向量，即通过枚举配电网每一种故障情况并根据故障情况进行停电时间和停电次数的计算，物理意义明确。
35.3、本发明与传统配电网可靠性计算方法相比，考虑了配电网中信息系统故障对配电网故障处理的影响，计算结果更为精确。
36.4、本发明与基于蒙特卡洛法的配电网可靠性计算方法相比，计算与收敛速度更快，计算结果更精确。
附图说明
37.为了更清楚地说明本发明的技术方案，下面将对实施例描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一个实施例，对于本领域普通技术人员来说，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
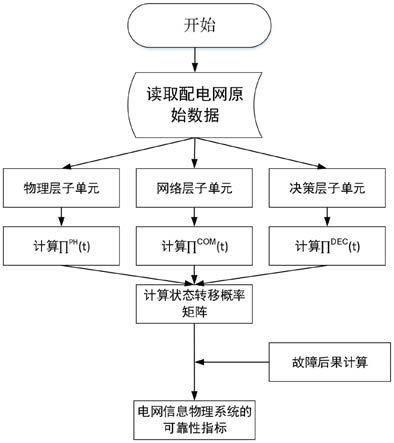
38.图1是本发明一种配电信息物理系统可靠性评估方法的流程图；
39.图2是本发明的配电信息物理系统的结构示意图；
40.图3是本发明的配电信息物理系统的拓扑图。
具体实施方式
41.下面结合本发明实施例中的附图，对本发明中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动的前提下所获得的所有其他实施例，都属于本发明保护的范围。
42.如图1所示，本发明所提供的配电信息物理系统可靠性评估方法包括以下步骤：
43.s1、根据配电网原始数据建立配电网信息物理系统的可靠性评估模型；
44.s2、对所述可靠性评估模型分成多个子单元，分别计算每一个单元的状态占用概率向量；具体的，可靠性评估模型分为：物理层、网络层以及决策层三个单元，对应的，状态占用概率向量∏
ph
(t)、∏
com
(t)、∏
dec
(t)；
45.s3、根据所述概率向量构建配电网信息物理系统的状态转移概率矩阵；
46.s4、根据所述状态概率转移矩阵计算各个子单元故障状态下的后果；
47.各个子单元故障状态下的后果包括停电时间和停电次数；
48.s5、根据所述后果计算电网信息物理系统的可靠性指标。
49.上述的配电信息物理系统cpds可靠性评估方法，通过将配电信息物理系统拆分为
三个互斥的子系统，分别计算各个子系统处于不同运行状态的概率，从而得到整个配电网信息物理系统在不同运行状态的概率。系统的每一种运行状态对应一种后果(停电次数与停电时间)，通过计算这些后果从而得出配电信息物理系统的可靠性指标。该配电信息物理系统可靠性评估方法物理意义明确、运算以及收敛速度快，克服了蒙特卡洛法仿真求解时间长、收敛速度慢的不足。
50.图2示出了配电信息物理系统的结构，配电网原始数据包括：配电网物理子系统和信息子系统的拓扑图以及配电网组成元件的故障率、修复时间。
51.具体的，步骤s1中，根据配电网原始数据建立配电网信息物理系统的可靠性评估模型包括元件建模和网络链路建模，即物理子系统和网络子系统。
52.在元件建模的过程中，通过“可用”和“不可用”两状态模型建立配电信息物理系统cpds中物理元件(如配电线路、变压器等)和信息元件(如传输线、交换机等)的可靠性模型。
53.网络链路建模的过程中，网络链路模型的可靠性通过拓扑可靠性c
o,p
(x)、延时可靠性d
o,p
(xi,y)以及无误可靠性判断e
o,p
(xi)。具体包括：
54.分析网络子系统的拓扑，形成可达矩阵，分析主站到各个ied的连通性，确定信道；
55.实际上，主站到一个特定ied的通信链路中可能存在多条信道，通过选出延时可靠性最高的一条信道作为最优信道，再对该信道进行误码可靠性的评估，从而完成对可靠性评估模型的建模评估，提高可靠性评估模型的可靠性。
56.一条信道xi的延时可靠性评估通过满足以下公式进行评估：
[0057][0058]
上式中，o,p分别为信道xi的始节点和末节点，y为默认延迟阈值，如果传输时间超过了y，那么信息传输失效。是信道延迟概率密度函数，相当于信道中各元件延迟概率密度函数的卷积，即：
[0059][0060]
上式中，f0(t)
…fp
(t)为信道xi中各元件延迟概率密度函数；
[0061]
一条信道xi的误码可靠性评估通过满足以下公式进行评估：
[0062][0063]
上式中，ek(xi)和e
k,k 1
(xi)分别表示信道xi中节点k和线路k,k 1传输没有发生错误的概率。
[0064]
步骤s2中，组成配电信息物理系统元件的故障率和修复率满足指数分布，与时间t无关，因此配电信息物理系统在组件故障下运行状态的演变表示为具有连续时间{x(t),t≥0}和离散状态s＝{0,1,2,
…
,n}的齐次马尔可夫过程。运行状态是指系统中所有组件的工作状态(可用或不可用)的集合。设定组成配电信息物理系统在时刻t的状态是x(t)＝i，由于组件故障，在时刻t δt的状态为x(t δt)＝j。那么配电信息物理系统在t时刻的状态为i且在t δt时刻状态为j的条件概率表示为：
[0065]
p{x(t δt)＝j|x(t)＝i}＝p{x(δt)＝j|x(0)＝i}
[0066]
上式中，i,j∈s。上式表示在t δt时刻处于状态j的概率仅取决于当前状态(当前时刻t的状态为i)，与时刻t之前的状态无关。条件概率也称为转移概率，即上式可表示为p
ij
(δt)。因此，一个系统在t1时刻处于状态j的概率表示为：
[0067]
其中
[0068][0069]
上式中，πj(t1)是系统在t1时刻处于状态j的概率质量函数(pmf)，也就是系统在t1时刻处于状态j的概率。πi(0)是系统在0时刻处于状态i的pmf，p
ij
(0,t1)表示系统在0时刻的状态为i且在t1时刻状态为j的条件概率，n代表系统的状态总数。因此，一个系统的状态占用概率向量π(t1)可以表示为：
[0070]
π(t1)＝[π1(t1) π2(t1)
…
πj(t1)
…
πn(t1)]
[0071]
给定系统的初始状态占用概率向量π(0)，这个状态占用概率向量通常表示系统处于正常工作状态的概率为1，其他故障状态的概率为0，那么π(t1)可以由以下式计算得出：
[0072][0073]
上式中，a表示系统的状态转移密度矩阵，用以下式来计算：
[0074]
其中
[0075]
i≠j且i,j∈[1,n]
[0076]
上式中，i,j为整数；n为系统的状态总数；q
ii
为在间隔开始时过程处于状态i的条件下，过程在δt期间不发生变化的概率；q
ij
为在间隔开始时过程处于状态i的条件下，过程在δt期间发生变化的概率，与引发该状态的部件的故障率或修复率有关；
[0077]
t矩阵为系统的状态转移概率矩阵，它与a矩阵的关系为：
[0078]
t＝a e
[0079]
上式中，e为单位矩阵。
[0080]
因此，物理层∏
ph
(t1)，网络层∏
com
(t1)和决策层∏
dec
(t1)三个子单元的状态占用概率向量表示为：
[0081][0082][0083][0084]
上式中，为物理层在t1时刻处于状态m的pmf；为网络层在t1时刻处于状态n的pmf；由于决策层仅由配电主站构成，是单元件系统，决策层的状态占用概率向量是一个二维向量，其中为决策层在t1时刻处于工作状态的pmf，为决策层在t1时刻处于失效状态的pmf。
[0085]
步骤s3中，cpds的状态转移概率矩阵mdrm的计算方式为：
[0086]
[0087]
上式中，mdrm矩阵是一个m
×
n矩阵，表示cpds中所有可能的运行状态组合。mdrm中的每个元素代表cpds处于三层持续时间的马尔科夫链(ctmc)单元组合状态的概率，从而可以对mdrm中每个元素对应的状态进行风险评估。
[0088]
步骤s4中，根据所述状态概率转移矩阵计算各个子单元故障状态下的后果，具体包括：
[0089]
s41、物理子系统的故障最多考虑到一阶，网络子系统也最多考虑到一阶故障，因此，按照配电网故障处理的过程，根据各最小隔离区与电源的连接关系将各最小隔离区分为四种情况，具体包括：
[0090]
s411、故障发生后，不受故障影响而与主电源保持连接的区域记为a类区域，所述a类区域内负荷的停运时间等于0；
[0091]
s412、故障发生后与主电源失去连接，然后在操作隔离开关隔离故障区域之后恢复与主电源之间连接的区域记为b类区域，所述b类区域内负荷的停运时间等于隔离开关的操作时间，记为tb；
[0092]
s413、故障发生后与主电源失去连接，然后在故障隔离之后，通过联络开关与备用电源连接而恢复通电的区域记为c类区域，所述c类区域内负荷的停运时间等于联络开关操作时间，记为tc；
[0093]
s414、直到故障排除后，才恢复供电的区域记为d类区域，所述d类区域内负荷的停运时间等于故障的修复时间，记为td；
[0094]
s42、当网络子系统发生故障时，故障引发的后果根据四种所述情况进行停电时间和停电次数的计算，并重新划分受影响的区域(b、c、d区域)，重新划分区域后再根据四种情况计算停电时间和停电次数，其中，重新划分受影响的区域包括以下步骤：
[0095]
s421、若网络故障导致故障与电源最小路上离故障最近的开关动作发生故障，则在所述最小路上的上游寻找最近的能动作的隔离开关；其中，所述电源最小路为故障与电源的最短路径。
[0096]
s422、若网络故障导致故障与联络开关最小路上离故障最近的开关动作发生故障，则在此最小路上往下游寻找最近的能动作的隔离开关即可；其中，所述联络开关最小路为故障与联络开关的最短路径。
[0097]
对cpds某一个特定状态，假设其物理层子单元状态为i，网络层子系统状态为j，则cpds处于状态(i，j)的概率为mdrm
(i，j)
(t1)，该情况下所有负荷停电时间总和为t
(i，j)
，所有负荷停电次数总和为n
(i，j)
。那么，cpds处于状态(i，j)的频率f
(i，j)
(t1)为：
[0098][0099]
其中，t
ph
为物理层子单元的状态转移概率矩阵，t
ph(k,i)
为该矩阵第k行，第i列的元素。
[0100]
步骤s5中，cpds的可靠性指标包括：配电网平均停电频率指标saifi、配电网平均停电持续时间指标saidi、平均供电可用率指标asai以及户平均停电持续时间指标caidi。计算方式分别如下：
[0101][0102][0103][0104][0105]
上式中，n为系统用户总数。
[0106]
下面结合具体配电网元件运行的具体参数数据对cpds可靠性计算作进一步的说明，本发明采用python程序编写cpds模型及其算法，以使本领域技术人员更了解本发明：
[0107]
本实施例cpds可靠性计算流程如图1所示，实施例物理子系统及网络子系统拓扑图如图3所示，实施例中物理子系统的参数如表1所示，信息子系统的参数如表2所示。负荷点a有250个用户，负荷点b有100个用户，负荷点c有50个用户。分段开关隔离切换时间为每次0.5小时，替代电源切换时间为1.0小时。
[0108]
表1物理子系统的参数
[0109][0110]
表2信息子系统的参数
[0111][0112][0113]
步骤s1中，读取配电网原始数据包括：组成配电网各元件两端节点、故障率以及平均修复时间等参数，建立配电网信息物理系统的可靠性评估模型。
[0114]
步骤s2中，t可取100s，表示电网处于稳态，根据上述计算公式，计算得出来的结果如下：
[0115]
∏
ph
(t)＝[0.99962,0.00000,0.00000,0.00000,0.00003,0.00006,0.00009,0.00000,0.00000,0.00000,0.00000,0.00000,0.00000,0.00003,0.00010,0.00007,0.00000]
[0116]
∏
com
(t)＝[0.96129,0.00006,0.00240,0.00240,0.00240,0.00120,0.00120,0.00240,0.00240,0.00240,0.00120,0.00120,0.00240,0.00240,0.00240,0.00120,0.00120,0.00006,0.00006,0.00006,0.00240,0.00240,0.00240,0.00120,0.00120]
[0117]
∏
dec
(t)＝[0.9999988,0.0000012]
[0118]
经过步骤s3的计算可以得出系统的mdrm矩阵为：
[0119]
mdrm＝[0.9609288415,0.0000640619,0.0024023221,0.0024023221,0.0024023221,0.0012011611,0.0012011611,0.0024023221,0.0024023221,0.0024023221,0.0012011611,0.0012011611,0.0024023221,0.0024023221,0.0024023221,0.0012011611,0.0012011611,0.0000640619,0.0000640619,0.0000640619,0.0024023221,0.0024023221,0.0024023221,0.0012011611,0.0012011611
[0120]
0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000
[0121]
0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,
0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000
[0122]
0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000
[0123]
0.0000274238,0.0000000018,0.0000000686,0.0000000686,0.0000000686,0.0000000343,0.0000000343,0.0000000686,0.0000000686,0.0000000686,0.0000000343,0.0000000343,0.0000000686,0.0000000686,0.0000000686,0.0000000343,0.0000000343,0.0000000018,0.0000000018,0.0000000018,0.0000000686,0.0000000686,0.0000000686,0.0000000343,0.0000000343
[0124]
0.0000548475,0.0000000037,0.0000001371,0.0000001371,0.0000001371,0.0000000686,0.0000000686,0.0000001371,0.0000001371,0.0000001371,0.0000000686,0.0000000686,0.0000001371,0.0000001371,0.0000001371,0.0000000686,0.0000000686,0.0000000037,0.0000000037,0.0000000037,0.0000001371,0.0000001371,0.0000001371,0.0000000686,0.0000000686
[0125]
0.0000822713,0.0000000055,0.0000002057,0.0000002057,0.0000002057,0.0000001028,0.0000001028,0.0000002057,0.0000002057,0.0000002057,0.0000001028,0.0000001028,0.0000002057,0.0000002057,0.0000002057,0.0000001028,0.0000001028,0.0000000055,0.0000000055,0.0000000055,0.0000002057,0.0000002057,0.0000002057,0.0000001028,0.0000001028
[0126]
0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000
[0127]
0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000
[0128]
0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000
[0129]
0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,
0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000
[0130]
0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000
[0131]
0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000
[0132]
0.0000329085,0.0000000022,0.0000000823,0.0000000823,0.0000000823,0.0000000411,0.0000000411,0.0000000823,0.0000000823,0.0000000823,0.0000000411,0.0000000411,0.0000000823,0.0000000823,0.0000000823,0.0000000411,0.0000000411,0.0000000022,0.0000000022,0.0000000022,0.0000000823,0.0000000823,0.0000000823,0.0000000411,0.0000000411
[0133]
0.0000987256,0.0000000066,0.0000002468,0.0000002468,0.0000002468,0.0000001234,0.0000001234,0.0000002468,0.0000002468,0.0000002468,0.0000001234,0.0000001234,0.0000002468,0.0000002468,0.0000002468,0.0000001234,0.0000001234,0.0000000066,0.0000000066,0.0000000066,0.0000002468,0.0000002468,0.0000002468,0.0000001234,0.0000001234
[0134]
0.0000658170,0.0000000044,0.0000001645,0.0000001645,0.0000001645,0.0000000823,0.0000000823,0.0000001645,0.0000001645,0.0000001645,0.0000000823,0.0000000823,0.0000001645,0.0000001645,0.0000001645,0.0000000823,0.0000000823,0.0000000044,0.0000000044,0.0000000044,0.0000001645,0.0000001645,0.0000001645,0.0000000823,0.0000000823
[0135]
0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000,0.0000000000]
[0136]
步骤s4仅取一例作为说明。以物理子系统中m2馈线故障，信息子系统未故障为例，计算得出该情况下全部负荷加起来的停电时间为325小时，停电次数为400次。
[0137]
步骤s5的计算结果如表3所示，比对考虑信息子系统前后的可靠性指标可以发现信息子系统的可靠性对cpds可靠性有一定影响。
[0138]
表3计算结果
[0139][0140][0141]
通过蒙特卡罗方法计算结果可验证本发明所述方法的可行性。由于本发明所述方法计算用时为0.5秒而蒙特卡洛方法计算用时为40.6小时，综上，本发明一种可靠性评估方法能可靠评估cpds的可靠性，有效提高计算速度，具有物理意义清晰等特点，运算以及收敛速度快，能够克服了蒙特卡洛法仿真求解时间长、收敛速度慢的不足。
[0142]
以上所揭露的仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到变化或变型，都应涵盖在本发明的保护范围之内。