一种基于广义协同高斯过程模型的结构不确定性量化解析方法与流程

1.本发明涉及工程结构不确定性量化领域，具体为基于广义协同高斯过程模型的结构不确定性量化解析方法。


背景技术：

2.土木工程的结构参数不可避免存在不确定性，可大致归纳为以下几个方面：结构材料物理特性的不确定性(如材料的弹性模量、质量密度的不确定性)；几何尺寸的不确定性(如构件的长度和截面高、宽度的不确定性)；结构边界条件的不确定性(如构件之间连接的不确定性)。引起结构参数不确定性的因素很多，比如加工容差、装配磨损、环境侵蚀、参数自身固有的随机性。传统的结构设计分析方法(如安全系数法)，一般将相关的不确定性参数当作确定量来考虑，再根据经验或以往资料确定安全系数的值，最终得到确定的计算结果。但参数不确定性必然导致结构响应具有不确定性，若简单地忽略这些不确定性，会造成对结构的认识不足，导致结构设计无法准确地反映结构的实际情况，可能会使结构处于一种不安全的状态。因此，为了提高工程结构的可靠度，为设计人员进行工程结构设计与决策提供更准确的信息，需要量化参数不确定性传递给结构的不确定性大小。
3.蒙特卡洛法(mcs)是常用的不确定性量化方法，需要对不确定性参数进行大量采样，然后进行相应的有限元模型计算，再对模型计算结果进行统计分析。mcs方法具有适用范围广、稳定性好、易实现的优点，但大量次数的有限元模型分析会导致计算成本很高，难以应用于大型复杂结构的不确定性量化。为克服mcs法计算效率低的不足，代理模型方法采用数学模型近似代替结构物理模型，后续不确定性量化无需原始物理模型，大大降低了计算成本。其中，一种基于高斯过程模型(gpm)的结构不确定性量化方法，将均值和方差的复杂高维积分问题转化为简单一维积分问题，得到了统计矩的解析结果。
4.gpm的建立涉及到训练样本，训练样本精度越高，建立的模型越准确。高精度样本数据的获取需要建立复杂的有限元模型，这在一定程度上也会增加计算成本，导致采用高精度样本建模效率较低。
5.综上所述，要通过较低的计算成本达到满意的建模精度，需要一种采用较少高精度样本数据就能获得良好预测精度的模型，以较低成本得到较高精度的统计矩计算结果，准确地量化结构不确定性大小。


技术实现要素：

6.本发明针对代理模型用来不确定性量化，存在高精度样本计算成本高和低精度样本建模精度低的问题，提出一种基于广义协同高斯过程模型(gc
‑
gpm)的结构不确定性量化解析方法。
7.本发明的目的是通过以下技术方案来实现的：一种基于广义协同高斯过程模型的结构不确定性量化解析方法，包括以下步骤：
8.a.获得高、低精度的训练样本集
9.a1.采样概率分布服从正态或均匀分布的结构不确定性参数，对于结构不确定性参数的概率分布不服从正态或均匀分布时，根据概率相等的原则将其转化为服从正态或均匀分布的参数u
i
后再采样，转化表达式如下：
[0010][0011]
其中，是参数x
i
的概率分布函数，g表示正态分布或均匀分布函数；然后通过拉丁超立方抽样获得结构不确定性参数的两组样本点，数量分别为n1和n2，将n1个样本点作为低精度输入值x1，n2个样本点作为高精度输入值x2，其中，n1＞n2；
[0012]
a2.在ansys中建立低精度和高精度的结构有限元模型，分别利用所述的低精度输入值x1和高精度输入值x2进行对应的有限元模型的循环计算，得到低精度观测值y1和高精度观测值y2，分别组成低精度训练样本集和高精度训练样本集
[0013]
b.利用所述的低精度训练样本集建立低精度高斯过程模型；具体为：
[0014]
将低精度训练样本集代入高斯过程模型进行建模，假定低精度高斯过程模型超参数为参数为表示低精度高斯过程模型的过程方差；l
1，k
表示当低精度输入值从x
1，k
到x
′
1，k
时低精度输出值y1的变化速度，l
1，k
越大，速度越慢，k表示向量的第k个维度，共有d维。根据最大化边缘似然函数mle得到超参数θ1，获得训练完成后的低精度高斯过程模型y1：
[0015][0016]
式中，表示高斯过程，和分别表示低精度高斯过程模型的预测值和预测方差，可写为：
[0017][0018][0019]
式中，c1＝c(x1，x1)是样本点集x1的协方差函数矩阵，表示低精度样本点之间的相关性；表示待预测点x
*
与低精度输入值x1之间的相关性，x
1，i
(i＝1，2，...，n1)表示组成低精度输入值x1的第i个样本点；e1表示长度为n1的单位向量。
[0020]
c.利用所述的高精度训练样本集建立差值高斯过程模型
[0021]
c1.假设最终预测值可由所述低精度高斯过程模型的预测值和一个高斯误差线性表示：
[0022][0023]
其中，y1(x)是低精度模型的真实值；y2(x)是高精度模型的真实值；δ2(x)表示高斯
过程误差；
⊥
表示相互独立；ρ1是一个比例系数，通过最大化边缘似然函数(mle)获得；
[0024]
c2.考虑步骤b中所述低精度高斯过程模型的预测值误差，预测值与真实值之间的关系可表示为：
[0025][0026]
其中，ε1(x)表示低精度高斯过程模型的预测值误差，对于两个不同的输入值，ε1(x)是相互独立的，即对任何x≠x
′
，有cov(ε(x)，ε(x
′
))＝0；y1(x)服从正态分布：
[0027]
c3.联立步骤c1和步骤c2中公式，可将y2(x)与ρ1y1(x)的差值δ2(x)表示为：
[0028][0029]
其中，δ2(x)服从正态分布：
[0030]
c4.将步骤c3中所述的记为δ
′2，将高精度训练样本集代入高斯过程模型的建立过程，假定差值高斯过程模型超参数为斯过程模型的建立过程，假定差值高斯过程模型超参数为表示差值高斯过程模型的过程方差；l
2，k
表示当高精度输入值从x
2，k
到x
′
2，k
时差值δ
′2的变化速度，l
2，k
越大，速度越慢，k表示向量的第k个维度，共有d维。根据mle得到超参数θ2，获得训练完成后的差值高斯过程模型：
[0031][0032]
式中，表示高斯过程，和分别表示差值高斯过程模型的预测值和预测方差，可写为：
[0033][0034][0035]
式中，c2＝c(x2，x2)是x2的协方差函数矩阵；表示低精度高斯过程模型在x2处的预测方差；表示待预测点x
*
与x2之间的相关性，x
2，i
(i＝1，2，...，n2)表示组成高精度输入值x2的第i个样本点；e2表示长度为n2的单位向量。
[0036]
d.利用低精度高斯过程模型和差值高斯过程模型共同构成广义协同高斯过程模型；具体为：
[0037]
将步骤b和步骤c所述的低精度高斯过程模型和差值高斯过程模型线性组合，共同
构成广义协同高斯过程模型，得到最终的高精度预测值和预测方差
[0038][0039][0040]
e.通过步骤d构建的广义协同高斯过程模型解析地计算结构响应的均值和方差；
[0041]
e1.根据统计原理，均值和方差的表达式为：
[0042][0043][0044]
式中，p(
·
)表示概率密度函数；x表示输入值；表示预测值，v
y
表示预测方差。
[0045]
通过将协方差函数分离为正态分布密度函数的形式，可将步骤d中所述和的不可积分形式转化为可积分形式：
[0046][0047]
[0048]
式中，α
1(2)，i(j)
表示α
1(2)
的第i(j)个元素；a
ji
表示第j行第i列的元素；b
ji
表示第j行第i列的元素；第j行第i列的元素；p
1(2)，i
表示p
1(2)
的第i个元素；q1＝c1e1，q2＝λ2e2，q
1(2)，j
表示q
1(2)
的第j个元素；d表示向量的维度；
[0049][0050]
x
k
表示x
*
的第k个元素；表示样本点集x
1(2)
第i(j)行、第k列的元素。
[0051]
e2.将步骤e1中所述的和代入和中，基于广义协同高斯过程模型，将均值和方差的高维积分转化为一维积分：
[0052]
[0053][0054]
e3.e2中所述的一维积分和可统一地表达为：
[0055][0056]
式中，表示均值为ζ，方差为的正态概率密度函数；p(x
k
)表示参数x
k
的概率密度函数。
[0057]
当参数为正态分布或均匀分布时，通过解析地计算一维积分，最终可以直接得到均值和方差的解析结果，量化结构不确定性大小，解析结果为：
[0058][0059]
式中，表示参数x
k
服从均值为ξ，方差为θ2的正态分布；表示参数x
k
服从上下限分别为和x的均匀分布；φ(
·
)表示标准正态概率分布函数。
[0060]
进一步地，在步骤c中，由于考虑了所述低精度高斯过程模型在所述高精度输入值x2处的预测误差ε1(x)，因此不需要满足嵌套样本数据的限制条件。
[0061]
进一步地，步骤a2中，根据结构的复杂程度，在ansys能够计算的条件下，将结构几何模型划分较少的单元作为低精度有限元模型，将划分单元数为低精度有限元模型的4
‑
5倍作为高精度有限元模型；或者将复杂原始模型作为高精度有限元模型，通过结构受力方式及自重相等进行等效简化的简单模型作为低精度有限元模型。通过低精度模型计算得到的低精度观测值与真实值偏差较大，因此称为低精度模型。
[0062]
进一步地，步骤b和步骤c4中，高斯过程模型的建立过程包括以下步骤：
[0063]
高斯过程模型表达式如下：
[0064][0065]
式中，表示高斯过程；m(x)为均值函数，采用常数形式μ；c(x，x
′
)为平方指数协方差函数，表示为：
[0066][0067]
式中，x和x
′
是输入值；x
k
与x
′
k
分别是x和x
′
的第k个元素，d表示输入值的维度；高斯过程模型的超参数定义为θ＝{l1，l2，...，l
k
，...，l
d
，η2}，η2表示过程方差；l
k
表示输出值在输入值从x
k
到x
′
k
时的变化速度，l
k
越大，速度越慢；
[0068]
假设有n个观测值的训练样本集其中，其中，根据模型输出y服从高斯分布的先验假设，则有：
[0069][0070]
同样的，待预测点x
*
处的预测值y
*
与y也服从高斯分布：
[0071][0072]
根据贝叶斯原理，预测值y
*
的后验分布为：
[0073]
将所述p(y)和p(y，y
*
)代入后验分布的计算公式，可得：
[0074][0075]
其中，
[0076][0077][0078]
式中，c＝c(x，x)；α＝c
‑1(y
‑
eμ
*
)；e表示长度为n的单位向量。
[0079]
其中，高斯过程模型的超参数θ＝{l1，l2，...，l
k
，...，l
d
，η2}可通过最大化边缘似然函数(mle)求得，即最小化负对数边缘似然函数
[0080][0081][0082]
本发明的优势是：
[0083]
1.相较于传统的蒙特卡洛方法，本发明提出的基于广义协同高斯过程模型(gc
‑
gpm)的结构不确定性量化解析方法采用数学模型代替结构物理模型，省去了大量原始模型计算，大大降低了计算成本，同时保证了计算结果有良好的精度；
[0084]
2.本发明采用整合了高、低精度样本数据的gc
‑
gpm，低精度样本用来拟合原始模型的整体趋势，较少的高精度样本用来对该趋势进行修正，以较低成本达到满意的建模精度，与一般的高斯过程模型(gpm)方法相比具有高效率的优势；
[0085]
3.本发明基于的gc
‑
gpm框架考虑了所述低精度高斯过程模型的预测值误差，相较于一般的多精度高斯过程模型，本发明适用范围更广，不仅适用于嵌套样本数据还适用于非嵌套样本数据
[0086]
4.本发明是基于gc
‑
gpm推导的结构不确定性量化解析方法，相较于使用一般的高斯过程模型和其他多精度高斯过程模型直接预测再统计预测结果，本发明所提解析方法能够快速直接地得到均值和方差的解析结果，准确量化结构的不确定性大小。
附图说明
[0087]
图1：基于gc
‑
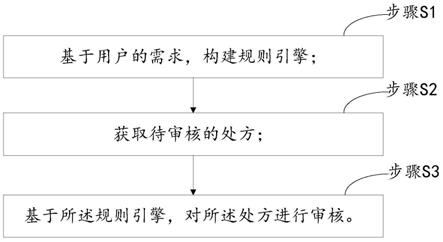
gpm的结构不确定性量化解析方法流程图；
[0088]
图2：gc
‑
gpm的建模步骤流程图；
[0089]
图3：单层球面壳的高低精度有限元模型。
具体实施方式
[0090]
下面结合一单层球面壳的固有频率统计矩计算进一步说明本发明。假定钢管直径、钢材密度和弹性模量为不确定性参数，分别服从均匀、正态和对数正态分布，计算不确定参数下网壳结构固有频率的均值和方差。利用本发明所提解析方法进行计算，具体包括以下步骤：
[0091]
a.获得高、低精度的训练样本集。
[0092]
a1.结构不确定性参数的概率分布包括但不限于正态分布、均匀分布、对数正态分布、威布尔分布、贝塔分布、伽马分布，将不服从正态或均匀分布的单层球面壳的结构不确定性参数(钢管直径、钢材密度和弹性模量)根据概率相等的原则转化为正态或均匀分布，再通过拉丁超立方抽样获得所述结构不确定性参数的两组样本点，数量分别为n1、n2，将n1个样本点作为低精度输入值x1，n2个样本点作为高精度输入值x2，其中，n1＞n2。本算例中，n1＝30，n2＝12；
[0093]
a2.利用所述的低精度输入值x1和高精度输入值x2进行对应的低精度有限元模型的循环计算，得到单层网壳固有频率的低精度数据y1和高精度数据y2，分别组成低精度训练样本集和高精度训练样本集本算例中，采用ansys软件建立该网壳的有限元模型，所有杆件均采用beam188梁单元模拟，根据结构的复杂程度，在ansys能够计算的条件下，将结构几何模型划分较少的单元作为低精度有限元模型，将划分单元数为低精度有限元模型的4
‑
5倍作为高精度有限元模型；或者将复杂原始模型作为高精度有限元模型，通过结构受力方式及自重相等进行等效简化的简单模型作为低精度有限元模型。通过低精度模型计算得到的低精度观测值与真实值偏差较大，因此称为低精度模型。高精度有限元模型将每根梁单元划分5个单元，共375个单元；低精度有限元模型将每个梁单元划分1个单元，共75个单元。高、低精度有限元模型如图3所示。
[0094]
b.利用所述的低精度训练样本集建立低精度高斯过程模型；具体为：
[0095]
高斯过程模型的建立过程包括以下步骤：
[0096]
高斯过程模型表达式如下：
[0097][0098]
式中，表示高斯过程；m(x)为均值函数，采用常数形式μ；c(x，x
′
)为平方指数协方差函数，表示为：
[0099][0100]
式中，x和x
′
是输入值；x
k
与x
′
k
分别是x和x
′
的第k个元素，d表示输入值的维度；高斯过程模型的超参数定义为θ＝{l1，l2，...，l
k
，...，l
d
，η2}，η2表示过程方差；l
k
表示输出值在输入值从x
k
到x
′
k
时的变化速度，l
k
越大，速度越慢；
[0101]
假设有n个观测值的训练样本集其中，其中，根据模型输出y服从高斯分布的先验假设，则有：
[0102][0103]
同样的，待预测点x
*
处的预测值y
*
与y也服从高斯分布：
[0104][0105]
根据贝叶斯原理，预测值y
*
的后验分布为：
[0106]
将所述p(y)和p(y，y
*
)代入后验分布的计算公式，可得：
[0107][0108]
其中，
[0109][0110][0111]
式中，c＝c(x，x)；α＝c
‑1(y
‑
eμ
*
)；e表示长度为n的单位向量。
[0112]
其中，高斯过程模型的超参数θ＝{l1，l2，...，l
k
，...，l
d
，η2}可通过最大化边缘似然函数(mle)求得，即最小化负对数边缘似然函数
[0113][0114][0115]
将低精度训练样本集代入高斯过程模型进行建模，假定低精度高斯过程模型超参数为参数为表示低精度高斯过程模型的过程方差；l
1，k
表示当低精度输入值从x
1，k
到x
′
1，k
时低精度输出值y1的变化速度，l
1，k
越大，速度越慢，k表示向量的第k个维度，共有d维。根据最大化边缘似然函数mle得到超参数θ1获得训练完成后的网壳固有频率的低精度高斯过程模型y1：
[0116][0117]
式中，表示高斯过程，和分别表示低精度高斯过程模型的预测值和预测方差，可写为：
[0118][0119][0120]
式中，c1＝c(x1，x1)是样本点集x1的协方差函数矩阵，表示低精度样本点之间的相关性；表示待预测点x
*
与低精度输入值x1之间的相关性，x
1，i
(i＝1，2，...，n1)表示组成低精度输入值x1的第i个样本点；e1表示长度为n1的单位向量。
[0121]
c.利用所述的高精度训练样本集建立差值高斯过程模型
[0122]
c1.假设最终预测值可由所述低精度高斯过程模型的预测值和一个高斯误差线性表示：
[0123][0124]
其中，y1(x)是网壳固有频率低精度模型的真实值；y2(x)是网壳固有频率高精度模的型真实值；δ2(x)表示高斯过程误差；
⊥
表示相互独立；ρ1是一个比例系数，通过最大化边缘似然函数(mle)获得；
[0125]
c2.考虑步骤b中所述网壳固有频率的低精度高斯过程模型的预测值误差，其预测值与真实值之间的关系可表示为：
[0126][0127]
其中，ε1(x)表示低精度高斯过程模型的预测值误差，对于两个不同的输入值，ε1(x)是相互独立的，即对任何x≠x
′
，有cov(ε(x)，ε(x
′
))＝0；y1(x)服从正态分布：考虑了所述低精度高斯过程模型在所述高精度输入值x2处的预测误差ε1(x)，不需要满足嵌套样本数据的限制条件。
[0128]
c3.联立步骤cl和步骤c2中公式，可将y2(x)与ρ1y1(x)的差值δ2(x)表示为：
[0129][0130]
其中，δ2(x)服从正态分布：
[0131]
c4.将步骤c3中所述的记为δ
′2，将高精度训练样本集代入高斯过程模型的建立过程，假定差值高斯过程模型超参数为斯过程模型的建立过程，假定差值高斯过程模型超参数为表示差值高斯过程模型的过程方差；l
2，k
表示当高精度输入值从x
2，k
到x
′
2，k
时差值δ
′2的变化速度，l
2，k
越大，速度越慢，k表示向量的第k个维度，共有d维。根据mle得到超参数θ2，获得训练完成后的差值高斯过程模型：
[0132][0133]
式中，表示高斯过程，和分别表示差值高斯过程模型的预测值和预测方差，可写为：
[0134][0135][0136]
式中，c2＝c(x2，x2)是x2的协方差函数矩阵；表示低精度高斯过程模型在x2处的预测方差；表示待预测点x
*
与x2之间的相关性，x
2，i
(i＝1，2，...，n2)表示组成高精度输入值x2的第i个样本点；e2表示长度为n2的单位向量。
[0137]
d.利用低精度高斯过程模型和差值高斯过程模型共同构成广义协同高斯过程模型；具体为：
[0138]
将步骤b和步骤c所述的网壳固有频率的低精度高斯过程模型和差值高斯过程模型线性组合，共同构成广义协同高斯过程模型，得到最终单层球面壳固有频率的高精度预测值和预测方差
[0139][0140][0141]
e.通过步骤d构建的单层球面壳固有频率的广义协同高斯过程模型解析地计算该网壳固有频率的均值和方差；
[0142]
e1.根据统计原理，均值和方差的表达式为：
[0143][0144][0145]
式中，p(
·
)表示概率密度函数；x表示输入值；表示预测值，v
y
表示预测方差。
[0146]
通过将协方差函数分离为正态分布密度函数的形式，可将步骤d中所述和的不可积分形式转化为可积分形式：
[0147][0148][0149]
式中，α
1(2)，i(j)
表示α
1(2)
的第i(j)个元素；a
ji
表示第j行第i列的元素；b
ji
表示第j行第i列的元素；第j行第i列的元素；p
1(2)，i
表示p
1(2)
的第i个元素；q1＝c1e1，q2＝λ2e2，q
1(2)，j
表示q
1(2)
的第j个元素；d表示向量的维度；
[0150][0151]
x
k
表示x
*
的第k个元素；表示样本点集x
1(2)
第i(j)行、第k列的元素。
[0152]
e2.将步骤e1中所述的和代入和和，基于广义协同高斯过程模型，将网壳固有频率均值和方差的高维积分转化为一维积分：
[0153]
[0154][0155]
[0156]
e3.e2中所述的一维积分和可统一地表达为：
[0157][0158]
式中，表示均值为ζ，方差为的正态概率密度函数；p(x
k
)表示参数x
k
的概率密度函数。
[0159]
当参数为正态分布或均匀分布时，通过解析地计算一维积分，最终可以直接得到均值和方差的解析结果，量化结构不确定性大小，解析结果为：
[0160][0161]
式中，表示参数x
k
服从均值为ξ，方差为θ2的正态分布；表示参数x
k
服从上下限分别为和x的均匀分布；φ(
·
)表示标准正态概率分布函数。
[0162]
在本算例中，得到该网壳结构固有频率的均值和方差的解析结果，并与mcs法对比，计算结果见表1。由表1可知，gc
‑
gpm法与mcs法的计算结果非常吻合，均值的最大误差仅为0.0070％，方差的最大误差仅为0.6295％。因此，gc
‑
gpm法对不确定性量化具有较高的计算精度。
[0163]
表1 gc
‑
gpm前5阶固有频率统计矩的计算结果及相对误差
[0164]
为进一步证明本发明所提解析方法的优势，将其与传统高斯过程模型(gpm)方法进行对比。分别采用15、25、35、45个高精度样本数据建立gpm，并计算该网壳前5阶固有频率的均值和方差，同时与mcs法对比，计算结果列于表2。由表1、2可知，要达到与12个高精度样本点的gc
‑
gpm法的计算精度相当，传统gpm法需要35个高精度样本点，而获取高精度样本的计算成本相对较高。以上分析表明，gc
‑
gpm法具有高精度低成本的优势。
[0165]
表2：gpm前5阶固有频率统计矩的计算结果及相对误差
[0166][0167][0168]
注：表中15h、25h、35h、45h分别表示15、25、35、45个高精度样本
[0169]
本说明书实施案例所述的内容仅仅是对发明构思的实现形式的列举，本发明的保护范围不应当被视为仅限于实施案例所陈述的具体形式，本发明的保护范围也包括本领域技术人员根据本发明构思所能够想到的等同技术手段。