一种基于观测器的连续网络化Lurie控制系统的鲁棒容错控制方法

一种基于观测器的连续网络化lurie控制系统的鲁棒容错控制方法
技术领域
1.本发明属于网络控制技术领域，尤其涉及事件触发机制下基于观测器的连续网络化lurie 控制系统的鲁棒容错控制方法。


背景技术：

2.随着计算机、通信和控制技术的迅速发展与广泛应用，网络控制系统(networked controlsystems,简记ncs)即各节点(传感器、控制器、执行器和被控对象)通过共享的通信网络传 输数据的控制系统备受关注。与传统的点对点控制系统相比，ncs具有安装成本低、易于维护、 灵活性高、可实现信息资源共享及远程操作简便等优点，目前已被广泛应用于智能医疗、智能 交通、智能制造等领域。但因ncs在应用中衍生出的时延、丢包、通讯资源浪费等问题，以及 实际生产过程会受到许多不确定因素的影响，如设备磨损、生产线老化等，系统不可避免地会 发生故障。系统一旦发生故障，就可能造成灾难性的损失甚至损害人身安全，因此借助容错控 制提高ncs运行的可靠性与稳定性，具有十分重要的经济意义和社会意义。
3.现有处理事件触发机制下具有时延的ncs的容错控制方法可分为两类。第一类主要针对传 感器到控制器之间的时延进行ncs的容错控制。得到了在执行器故障下闭环系统随机均方稳定 的性能以及容错控制器与事件触发机制的联合设计方法。第二类主要研究了传感器到控制器和 控制器到执行器之间均具有时延的ncs的容错控制。将传感器到控制器网络中的时延和控制器 到执行器网络中的时延合并为总时延，并结合李雅普诺夫稳定性理论设计了容错控制器增益和 事件触发参数，以保证故障系统的所需性能，减少通信资源的浪费。目前针对事件触发机制下 具有时延的ncs的容错控制方法还不完善，关于传感器到控制器和控制器到执行器之间均具 有时延的ncs容错控制方法还需要进一步分析。现有技术存在的问题是：
4.1)多数技术仅考虑控制器到执行器的时延或者将传感器到控制器、控制器到执行器之间的 时延合并到一起处理，并假设系统的状态可测，缺乏基于观测器的将传感器到控制器、控制 器到执行器的时延分别进行处理的容错控制器的设计方法；
5.2)多数技术缺乏同时考虑时延、系统参数的不确定性、执行器故障等因素，并未建立事 件触发机制下网络化lurie控制系统模型，并未在同一框架内对时延、不确定性、事件触发 机制和执行器故障对网络化lurie控制系统性能的影响进行分析；
6.3)根据lyapunov稳定性理论，具有双侧时延的闭环系统稳定性条件，事件触发权重矩阵、 鲁棒容错控制器和观测器的联合设计方法需要进一步研究。
7.解决上述技术问题的意义：
8.考虑传感器到控制器之间以及控制器到执行器之间均具有时延和不确定性的网络化lurie 控制系统，设计鲁棒容错控制器，使得系统执行器发生故障时，能够对故障有效的容错并使系 统保持稳定，对于推动ncs理论的应用有重要的实际意义。通过在控制器节
点上构造一个观 测器，建立基于观测器的事件触发机制数学模型，在保证闭环系统稳定的同时还可以减少网络 中的数据传输量，进而节约网络带宽资源。根据lyapunov稳定性理论，推导出闭环系统稳定的 充分条件，进而实现事件触发机制、容错控制器与观测器的协同设计。


技术实现要素：

9.针对现有技术存在的问题，本发明提供了一种基于观测器的连续网络化lurie控制系统的 鲁棒容错控制方法，包括以下步骤：
10.步骤1：建立起闭环系统数学模型：
11.考虑如下含有不确定性与执行器故障的lurie系统：
[0012][0013]
其中，x(t)∈rn,u(t)∈rm,y(t)∈rq分别为系统状态向量、输入向量和输出向量；a,b,c,d为合适 维数的实常矩阵，δa,δb,δd为范数有界的不确定性矩阵，且满足[δa δb δd]＝uξ(t)[h
1 h
2 h3]， 其中u,h1,h2,h3为具有适当维数的已知矩阵，ξ(t)为满足ξ(t)
t
ξ(t)＜i的未知矩阵；f为执行 器故障指示矩阵，满足f＝diag{f1,f2,
…fm
}，fj∈[0,1],j＝1,2,
…
m，其中，fj＝0表示第j个 执行器完全失效，fj＝1表示第j个执行器正常工作，fj∈(0,1)表示第j个执行器部分失效； ψ(
·
):rq→rq
为无记忆非线性函数，满足局部lipschitz条件，ψ(0)＝0，且对于任意的y(t)∈rq满足如下扇形区条件：
[0014]
ψ
t
(y(t))[ψ(y(t))-θy(t)]≤0
ꢀꢀ
(2)
[0015]
其中，θ为实对角矩阵，通常称这样的非线性函数ψ(
·
)属于扇形区域[0,θ]，记为ψ(
·
)∈l[0,θ]；
[0016]
采样器以固定的周期h采集系统的输出信号，采样器采集的信号会直接传给与它相连的事 件发生器，事件发生器是否能将采样数据y(tkh jh)发送给控制器需要根据条件(3)来判断：
[0017]
[y(tkh jh)-y(tkh)]
t
v[y(tkh jh)-y(tkh)]＞σy
t
(tkh jh)vy(tkh jh)
ꢀꢀꢀ
(3)其中，v是一个正定矩阵，j∈z

,σ∈[0,1]；
[0018]
当事件发生器释放了当前采样信号后，采样信号直接经网络传给零阶保持器，进而经由观 测器传给执行器，在此过程中，由于网络的存在，信号在传输过程中会有时延，用表示从传 感器到控制器的时延,表示从控制器到执行器的时延，对任意的t≥0均有 [0019]
将事件发生器发送数据的时刻记为i0h,i1h,i2h,
…
,其中i0h＝0是初始触发时刻，由于时延的存 在，释放的信号到达观测器的时刻为另外，事件发生器发送数据的周 期可表示为
[0020]
观测器端收到的系统输出为：
[0021][0022]
对于分两种情况进行讨论：
[0023]
第一种情况：如果定义
[0024][0025]
可得
[0026][0027]
相应地，定义一个误差向量：
[0028]
θk(t)＝0
ꢀꢀꢀ
(7)
[0029]
第二种情况：若因为存在一个正整数ε≥1使得
[0030][0031]
为了简化表达，令：
[0032][0033]
然后区间就可以被分成下面ε 1个子区间
[0034][0035]
定义分段函数
[0036][0037]
由(9)、(10)可以得到
[0038][0039]
定义误差向量为
[0040][0041]
从θk(t)的定义可知，时可以得到(13)及(14)
[0042]
y(ikh)＝θk(t) y(t-ρ(t))
ꢀꢀꢀ
(13)
[0043][0044]
在控制器端构造如下形式的观测器：
[0045][0046]
其中代表观测器的状态，代表观测器的输出，l是待设计的观测器增益矩阵；
[0047]
采用如下基于观测器的反馈控制律：
[0048][0049]
式中k为控制器增益矩阵；
[0050]
由于控制器到执行器网络中存在时延控制对象的输入不同于观测器的输入，
(17)成立：
[0051][0052]
定义误差向量增广向量z(t)＝[x
t
(t) e
t
(t)]
t
，，闭环网络控制系统可以写成如下形式：
[0053][0054]
其中，c1＝[0 c],k1＝[-k k],
[0055][0056]
此时，条件(2)变为
[0057][0058]
其中，
[0059]
步骤2：考虑传感器到控制器和控制器到执行器时延对闭环系统参数的影响，对闭环系统(18) 进行稳定性分析：
[0060]
对于给定的标量h1,h2,h3,h4,σ，执行器故障指示矩阵f，增益矩阵k和l，如果存在合适 维数的矩阵m,n和正定矩阵w＞0,v＞0,si＞0,pi＞0,i＝1,2,3,4,满足(20)及(21)：
[0061][0062][0063]
其中，
[0064][0065][0066][0067][0068][0069]
φ
34
＝-m p2，φ
44
＝-s
2-p2，
[0070]
φ
55
＝-2p4 n n
t
,φ
56
＝p
4t-n
t
,φ
57
＝p
4-n,φ
66
＝-s
3-p
3-p4,φ
77
＝-s
4-p4,
[0071]
则lurie系统(18)在l[0,θ]内是鲁棒绝对稳定的；
[0072]
步骤3：给出事件触发机制下观测器和控制器的联合设计方法：
[0073]
对于给定的标量h1,h2,h3,h4,σ，执行器故障指示矩阵f，增益矩阵k和l,如果存在合适维 数的矩阵y1,y2和正定矩阵x＞0,v＞0,y＞0,满足(29)及(30):
[0074][0075][0076]
其中，
[0077][0078][0079][0080][0081][0082]
i1＝[-i i]，i2＝[0 i]，
[0083]
则lurie系统(18)在l[0,θ]内是鲁棒绝对稳定的，控制器增益矩阵k，观测器增益矩阵l，事 件触发权重矩阵v可由(31)给出：
[0084]
k＝y1x-1
,l＝y2x-1c
,v＝c
t
x-1
yx-1c
。
ꢀꢀ
(31)
[0085]
本发明的有益效果为：针对一类传感器到控制器和控制器到执行器均具有时延的不确定性 连续网络化lurie控制系统，研究了其在执行器故障下基于事件触发机制的观测器与容错控制器 的协同设计问题。首先考虑系统的状态不能直接测量，在控制器节点上构造了一个观测器。其 次，为减少网络带宽资源浪费，提高网络控制系统运行性能，提出了一种基于事件触发机制的 网络控制系统方法。通过引入事件触发机制和执行器故障指示矩阵，利用状态增广技术将lurie 网络化控制系统建模为一个多时滞的lurie系统，获得闭环系统的模型。最后，根据lyapunov 稳定性理论，推导出闭环系统稳定的充分条件，并给出了容错控制器和观测器的设计方法，所 得到的结果都是以线性矩阵不等式的形式给出的，便于利用线性矩阵不等式工具箱进行求解。
附图说明
[0086]
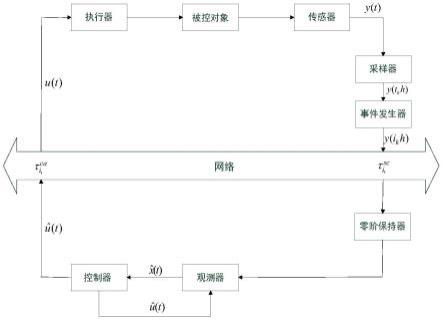
图1是本发明实施例提供的事件触发机制下基于观测器的ncs结构图。
[0087]
图2是本发明实施例提供的执行器正常时事件触发时间间隔图。
[0088]
图3是本发明实施例提供的执行器正常时系统状态x1(t)及其估计值图。
[0089]
图4是本发明实施例提供的执行器正常时系统状态x2(t)及其估计值图。
[0090]
图5是本发明实施例提供的执行器故障时事件触发时间间隔图。
[0091]
图6是本发明实施例提供的执行器故障时系统状态x1(t)及其估计值图。
[0092]
图7是本发明实施例提供的执行器故障时系统状态x2(t)及其估计值图。
具体实施方式
[0093]
考虑如下含有不确定性与执行器故障的lurie系统：
[0094][0095]
其中，x(t)∈rn,u(t)∈rm,y(t)∈rq分别为系统状态向量、输入向量和输出向量；a,b,c,d为合适 维数的实常矩阵，δa,δb,δd为范数有界的不确定性矩阵，且满足[δa δb δd]＝uξ(t)[h
1 h
2 h3], 其中u,h1,h2,h3为具有适当维数的已知矩阵，ξ(t)为满足ξ(t)
t
ξ(t)＜i的未知矩阵；f为执行 器故障指示矩阵，满足f＝diag{f1,f2,
…fm
},fj∈[0,1],j＝1,2,
…
m，其中，fj＝0表示第j个 执行器完全失效，fj＝1表示第j个执行器正常工作，fj∈(0,1)表示第j个执行器部分失效； ψ(
·
):rq→rq
为无记忆非线性函数，满足局部lipschitz条件，ψ(0)＝0，且对于任意的y(t)∈rq满足如下扇形区条件：
[0096]
ψ
t
(y(t))[ψ(y(t))-θy(t)]≤0
ꢀꢀ
(2)
[0097]
其中，θ为实对角矩阵，通常称这样的非线性函数ψ(
·
)属于扇形区域[0,θ]，记为ψ(
·
)∈l[0,θ]；
[0098]
注1：对于更一般的情况ψ(
·
)∈l[θ1,θ2]，总可以通过环路变换转化为ψ(
·
)∈l[0,θ]的情况， 故本发明只考虑ψ(
·
)∈l[0,θ]的情况；
[0099]
图1所示的ncs结构图由执行器、被控对象、传感器、采样器、零阶保持器、观测器、事 件发生器、控制器组成。采样器以固定的周期h采集系统的输出信号。采样器采集的信号会直 接传给与它相连的事件发生器，然后，事件发生器是否能将采样数据y(tkh jh)发送给控制器需 要根据如下条件来判断：
[0100]
[y(tkh jh)-y(tkh)]
t
v[y(tkh jh)-y(tkh)]＞σy
t
(tkh jh)vy(tkh jh)
ꢀꢀ
(3)
[0101]
其中，v是一个正定矩阵，j∈z

,σ∈[0,1]；
[0102]
注2：只有满足式(3)的输出采样数据y(tkh jh)才会被传输，很显然这个事件触发机制 将会降低网络中的通信负载，降低控制器的计算量，有一种特殊情况，如果式(3)中σ＝0， 则对所有的采样输出数据y(tkh jh)式(3)都成立，此时，事件触发机制将退化为时间触发机 制，另外，本发明所采用的事件触发机制触发时刻是基于系统采样周期h的，只有在采样时刻 才有可能触发，保证了最小事件间隙时间为正，避免了芝诺行为；
[0103]
当事件发生器释放了当前采样信号后，采样信号直接经网络传给零阶保持器，进而经由观 测器传给执行器，在此过程中，由于网络的存在，信号在传输过程中会有时延，用
表示从传 感器到控制器的时延,表示从控制器到执行器的时延；
[0104]
为了方便于分析，提出以下合理假设：
[0105]
(a)矩阵c是行满秩矩阵；
[0106]
(b)假设传感器采用时间驱动，控制器和执行器采用事件驱动，数据采用单包传输；
[0107]
(c)系统时延和都是有界的,即对任意的t≥0均有
[0108]
将事件发生器发送数据的时刻记为i0h,i1h,i2h,
…
,其中i0h＝0是初始触发时刻，由于网络时延 的存在，那些释放的信号到达观测器的时刻为另外，事件发生器发送 数据的周期可表示为
[0109]
基于上述分析观测器端收到的系统输出：
[0110][0111]
对于分两种情况进行讨论：
[0112]
第一种情况：如果定义
[0113][0114]
可得
[0115][0116]
相应地，定义一个误差向量：
[0117]
θk(t)＝0
ꢀꢀꢀ
(7)
[0118]
第二种情况：若因为很容易证明存在一个正整数ε≥1使得
[0119][0120]
为了简化表达，令：
[0121][0122]
然后区间就可以被分成下面ε 1个子区间
[0123][0124]
定义分段函数
[0125][0126]
由(9)、(10)可以得到
[0127][0128]
这时，定义误差向量
[0129][0130]
从θk(t)的定义可知，时可以得到以下式子成立
[0131]
y(ikh)＝θk(t) y(t-ρ(t))
ꢀꢀꢀ
(13)
[0132][0133]
在控制器端构造一个如下形式的观测器：
[0134][0135]
其中代表观测器的状态，代表观测器的输出，l是待设计的观测器增益矩阵；
[0136]
采用如下基于观测器的反馈控制律：
[0137][0138]
式中k为控制器增益矩阵；
[0139]
注3：由于控制器到执行器网络中存在时延控制对象的输入不同于观测器的输入，下 面式子成立：
[0140][0141]
定义误差向量增广向量z(t)＝[x
t
(t) e
t
(t)]
t
，，基于以上分析，闭环网络控制系统可以写成如下形式：
[0142][0143]
其中，
[0144][0145][0146]
此时，条件(2)变为
[0147][0148]
其中，
[0149]
注4：在实际工业系统中，执行器故障指示矩阵f＝diag{0,0}代表执行器是完全失效的， 控制器将无法实现对被控对象的控制，因此，只考虑执行器部分失效的情况，即执行器即使失 效了，但仍能在一定范围内正常工作。
[0150]
定义1：如果对于所有的ψ(
·
)∈l[0,θ]，lurie系统(18)都是全局渐近稳定的，则称其在l[0,θ] 内是绝对稳定的。
[0151]
定理1：考虑如图1所示的系统，对于给定的标量h1,h2,h3,h4,σ，执行器故障指示矩阵f，增益 矩阵k和l,如果存在合适维数的矩阵m,n和正定矩阵w＞0,v＞0,si＞0,pi＞0,i＝1,2,3,4,满足 下列不等式
[0152][0153][0154]
其中，
[0155][0156][0157][0158][0159]
φ
22
＝-s
1-p
1-p2，φ
23
＝-m p2，
[0160]
φ
34
＝-m p2，φ
44
＝-s
2-p2，φ
55
＝-2p4 n n
t
，φ
56
＝p
4t-n
t
，
[0161]
φ
57
＝p
4-n,φ
66
＝-s
3-p
3-p4,φ
77
＝-s
4-p4.
[0162]
则lurie系统(18)在l[0,θ]内是鲁棒绝对稳定的。
[0163]
证明：构造一个lyapunov-krasovskii泛函
[0164]
v(t,z(t))＝v1(t,z(t)) v2(t,z(t)) v3(t,z(t)).
ꢀꢀ
(22)
[0165]
其中，
[0166]v1
(t,z(t))＝z
t
(t)wz(t),
[0167][0168][0169]
沿系统(18)对v(t,z(t))求导，
[0170][0171]
其中，
[0172][0173]
[0174][0175]
应用引理1和引理2来处理(23)式中的积分项，可以得到
[0176][0177][0178][0179][0180]
其中，
[0181][0182][0183]
将(24)，(25)，(26)，(27)代入(23)，结合式(14)及式(19)可得
[0184][0185]
其中由schur 补引理和定义1得，若式(28)小于0可知lurie系统(18)对任意的l[0,θ]都是全局渐近稳定 的，因而是绝对稳定的，定理1证毕。
[0186]
定理2：考虑如图1所示的系统，对于给定的标量h1,h2,h3,h4,σ，执行器故障指示矩阵f，增益 矩阵k和l,如果存在合适维数的矩阵y1,y2和正定矩阵 x＞0,v＞0,y＞0,满足下列不等式
[0187]
[0188][0189]
其中，
[0190][0191][0192][0193][0194][0195]
i1＝[-i i]，i2＝[0 i].
[0196]
则lurie系统(18)在l[0,θ]内是鲁棒绝对稳定的,控制器增益矩阵k,观测器增益矩阵l,事件触 发权重矩阵v可由下式求取
[0197]
k＝y1x-1
,l＝y2x-1c
,v＝c
t
x-1
yx-1c
.
ꢀꢀ
(31)
[0198]
证明：由schur补引理及引理3可知可转化为
[0199][0200]
其中，
[0201][0202]
λ
22
＝diag{-p1，-p2，-p3，-p4，-si，-s-1
i}，
[0203][0204]
[0205]
φ
22
＝-s
1-p
1-p2，φ
23
＝-m p2，φ
34
＝-m p2， φ
44
＝-s
2-p2，φ
55
＝-2p4 n n
t
，φ
56
＝p
4t-n
t
，φ
57
＝p
4-n，φ
66
＝-s
3-p
3-p4，φ
77
＝-s
4-p4，
[0206]
由于中存在非线性项，不便控制器的求解，因此取定义定义
[0207]
在矩阵两边分别左乘右乘注意 到由于必有
[0208][0209]
式(33)等价于
[0210][0211]
即可得到线性矩阵不等式(29)成立，其中k＝y1x-1
,l＝y2x-1c
,v＝c
t
x-1
yx-1c
，定理2证毕。
[0212]
注5：由于矩阵c是m
×
n的行满秩矩阵，则存在n
×
m的矩阵c

使得cc

＝i,c

称为c的 右逆，由y2＝lcx可得观测器增益矩阵l＝y2x-1c
。
[0213]
注6：由于x＞0,v＞0,cx≠0,c行满秩，所以必然存在(cx)
t
v(cx)＞0,即y＝xc
t
vcx为 非奇异矩阵，可得事件触发权重矩阵v＝c
t
x-1
yx-1c
。
[0214]
仿真算例
[0215]
为了验证算法的有效性和可用性，考虑如下的lurie系统，其中
[0216][0217][0218]
显然此系统不稳定。
[0219]
根据定理2，当其他参数的选取不变时，系统所允许的时延上界随事件触发阈值σ变化的 规律如表1所示。
[0220]
表1不同事件触发阈值σ下的或
[0221][0222]
从表1可以看到，事件阈值σ越小，所允许的系统时延上界越大。因此，为了减轻时延对 系统性能的影响，可以适当减小事件阈值σ。
[0223]
假设事件触发阈值σ＝0.1，系统采样周期h＝0.01s，时延 h1＝0.01,h2＝0.11,h3＝0.01,h4＝0.11。取非线性函数ψ(
·
)为饱和函数sat(
·
)，系统初始状态取为 x(0)＝[-0.8 0.8]
t
,
[0224]
根据定理2，给定故障指示矩阵可求得系统正常运行时的控制器增益矩阵、观 测器增益矩阵及事件触发权重矩阵为：
[0225][0226]
事件触发时间间隔如图2所示，系统的状态曲线如图3-图4所示。
[0227]
给定故障指示矩阵可求得系统执行器故障时的控制器增益矩阵、观测器增益矩 阵及事件触发权重矩阵为：
[0228][0229]
事件触发时间间隔如图5所示，系统的状态曲线如图6-图7所示。
[0230]
由图2和图5可以看出，系统在平衡点附近，需传输的数据较暂态过程中要少得多，这恰 好符合按控制需求传输数据的期望，较时间触发机制而言，可有效地节约网络通讯资源，减少 浪费，节省资源。由图6-图7可以看出，在执行器发生故障时，系统通过有效的容错控制，依 旧可以稳定。
[0231]
本发明针对传感器到控制器之间以及控制器到执行器之间均具有时延和不确定性的网络化 lurie控制系统，设计了鲁棒容错控制器，使得系统执行器发生故障时，能够对故障有效的容错 并使系统保持稳定。通过在控制器节点上构造了一个观测器，建立了基于观测器的事件触发机 制数学模型，在保证闭环系统稳定的同时还减少了网络中的数据传输量，进而节约了网络带宽 资源。根据lyapunov稳定性理论，推导出闭环系统稳定的充分条件，实现事件触发机制、容错 控制器与观测器的协同设计。
[0232]
以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则 之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。