一种增益受限不确定分数阶混沌系统的保密通信方法

1.本发明涉及保密通信技术领域，特别是涉及一种增益受限不确定分数阶混沌系统的保密通信方法。


背景技术：

2.在通常的控制设计当中，控制方向一般是需要预先获知的，当控制方向不确定时，特别当控制系数是时变或是缓变时，不仅混沌系统的同步控制问题会变得非常困难，原本稳定的系统也可能会失去稳定。因此控制方向未知的情况也是工程实践方面设计者们必须考虑的问题。
3.从理论的角度分析，增益越大，系统的动态响应性能越好，响应速度也越快，鲁棒性越强。但是，在实际应用中，不建议使用高增益，这是因为高增益会使得控制难以实现，也会使得控制成本更高，同时，过高的增益会使系统变得不够稳定，抗干扰能力降低，也会放大噪声，如何同时综合考虑不确定性(控制方向未知)和增益受限成为本领域亟需解决的技术问题。


技术实现要素：

4.基于此，本发明的目的是提供一种增益受限不确定分数阶混沌系统的保密通信方法，以实现同时考虑控制方向未知和增益受限。
5.为实现上述目的，本发明提供了一种增益受限不确定分数阶混沌系统的保密通信方法，所述方法包括：
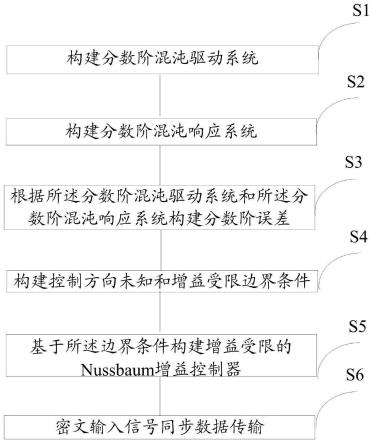
6.步骤s1：构建分数阶混沌驱动系统；
7.步骤s2：构建分数阶混沌响应系统；
8.步骤s3：根据所述分数阶混沌驱动系统和所述分数阶混沌响应系统构建分数阶误差；
9.步骤s4：构建控制方向未知和增益受限的边界条件；
10.步骤s5：基于所述边界条件构建增益受限的nussbaum增益控制器；
11.步骤s6：密文输入信号同步数据传输；传输密文输入信号时，分数阶混沌驱动系统输出混沌驱动输入信号，并通过第一通道传输所述混沌驱动输入信号，所述混沌驱动输入信号经过所述nussbaum增益控制器和所述分数阶混沌响应系统后生成响应输出信号，加密函数利用所述混沌驱动输入信号对所述密文输入信号进行掩盖后生成秘钥，并通过第二通道传输至解密函数，解密函数根据所述响应输出信号和秘钥进行解密，生成解密后的密文输入信号。
12.可选地，所述构建分数阶混沌驱动系统，具体公式为：
13.d
α
x＝f(x)θ
x
f(x)
ꢀꢀ
(1)；
14.其中，d
α
x表示分数阶导数，f(x)∈rn×m为系统函数矩阵，θ
x
∈rm为驱动系统的实际值，f(x)∈rn为已知或未知的非线性函数向量，x为系统的混沌驱动输入信号。
15.可选地，所述构建分数阶混沌响应系统，具体公式为：
16.d
α
y＝g(y)θy g(y) bu
ꢀꢀ
(2)；
17.其中，y∈rn为系统的响应输出信号，g(y)∈rn×m为函数矩阵，θy∈rm为响应系统的实际值，g(y)∈rn为已知或未知的非线性函数向量，b为未知控制系数，u为控制输入，d
α
y为分数阶导数。
18.可选地，所述根据所述分数阶混沌驱动系统和所述分数阶混沌响应系统构建分数阶误差，具体公式为：
[0019][0020]
其中，e为误差向量，y∈rn为系统的响应输出信号，g(y)∈rn×m为函数矩阵，θ
x
∈rm为驱动系统的实际值，θy∈rm为响应系统的实际值，θ
x
∈rm和θy∈rm均为未知的参数向量，g(y)∈rn为已知或未知的非线性函数向量，b为未知控制系数，u为控制输入，f(x)∈rn×m为系统函数矩阵，f(x)为已知或未知的非线性函数向量，x为系统的混沌驱动输入信号。
[0021]
可选地，所述基于所述边界条件构建增益受限的nussbaum增益控制器，具体公式为：
[0022][0023]
其中，为驱动系统的估计值，为响应系统的估计值，θ
x
为驱动系统的实际值，θy为的响应系统的实际值，s为分数阶积分滑模曲面，u为控制输入，f(x)为系统函数矩阵，f(x)为已知或未知的非线性函数向量，g(y)为响应系统函数矩阵，g(y)为已知或未知的非线性函数向量，e为误差向量，r1、r2均为滑模系数，s为分数阶积分滑模曲面，n(k)为nussbaum函数，k为nussbaum增益，为nussbaum增益的调节律，h为增益边界，l为nussbaum增益的调节律变量，c为系数矩阵，ud为控制率。
[0024]
可选地，所述方法还包括：
[0025]
步骤s7：验证nussbaum增益控制器的增益受限，具体包括：
[0026]
步骤s71：构建分数阶积分滑模曲面；
[0027]
步骤s72：基于线性频率分布模型确定滑模面的等价频率分布模型；
[0028]
步骤s73：基于滑模面的等价频率分布模型构建第一lyapunov函数的导数；
[0029]
步骤s74：利用所述nussbaum增益控制器对所述第一lyapunov函数的导数进行化简，获得化第一简化导数；
[0030]
步骤s75：基于自适应律分别构建驱动系统的频率分布模型和响应系统的频率分布模型；
[0031]
步骤s76：基于所述驱动系统的频率分布模型和所述响应系统的频率分布模型构建第二lyapunov函数的导数；
[0032]
步骤s77：将所述第一简化导数和所述第二lyapunov函数的导数进行求和简化，获得第二简化导数；
[0033]
步骤s78：将所述第二简化导数进一步简化，获得第三简化导数；
[0034]
步骤s79：对所述第三简化导数两边积分，获得积分公式。
[0035]
可选地，所述将所述第一简化导数和所述第二lyapunov函数的导数进行求和简化，获得第二简化导数，具体公式为：
[0036][0037]
其中，为第二简化导数，分别为的简写，为第一简化导数，为第二lyapunov函数的导数，为驱动系统的实际值θ
x
与驱动系统的估计值之间的差值，为响应系统的实际值θy与响应系统的估计值之间的差值，s为分数阶积分滑模曲面，r1、r2均为滑模系数，f(x)为系统函数矩阵，g(y)为响应系统函数矩阵，n(k)为nussbaum函数，k为nussbaum增益，b为未知控制系数，为nussbaum增益的调节律，μ(ω)为权重函数，z(ω,t)∈r为实际误差变量，ω为频率分布模型中的变量。
[0038]
可选地，所述利用所述nussbaum增益控制器对所述第一lyapunov函数的导数进行化简，获得化第一简化导数，具体公式为：
[0039][0040]
其中，为第一简化导数，为驱动系统的实际值θ
x
与驱动系统的估计值之间的差值，为响应系统的实际值θy与响应系统的估计值之间的差值，s为分数阶积分滑模曲面，r1、r2均为滑模系数，f(x)为系统函数矩阵，g(y)为响应系统函数矩阵，n(k)为nussbaum函数，k为nussbaum增益，b为未知控制系数，为nussbaum增益的调节律，μ(ω)为权重函数，z(ω,t)∈r为实际误差变量，ω为频率分布模型中的变量。
[0041]
可选地，所述基于所述驱动系统的频率分布模型和所述响应系统的频率分布模型构建第二lyapunov函数的导数，具体公式为：
[0042][0043]
其中，为第二lyapunov函数的导数，ω为频率分布模型中的变量，μ(ω)为权重函数，均为函数，均为估计误差的分数阶形式，为驱动系统的实际值θ
x
与驱动系统的估计值之间的差值，为响应系统的实际值θy与响应系统的估计值之间的差值，f(x)为系统函数矩阵，g(y)为响应系统函数矩阵，s为分数阶积分滑模曲面。
[0044]
可选地，所述密文输入信号为视频、语音、图像、军事命令、资料文件中至少一种。
[0045]
根据本发明提供的具体实施例，本发明公开了以下技术效果：
[0046]
本发明公开一种增益受限不确定分数阶混沌系统的保密通信方法，传输密文输入信号时，分数阶混沌驱动系统输出混沌驱动输入信号，并通过第一通道传输所述混沌驱动输入信号，所述混沌驱动输入信号经过所述nussbaum增益控制器和所述分数阶混沌响应系统后生成响应输出信号，加密函数利用所述混沌驱动输入信号对所述密文输入信号进行掩盖后生成秘钥，并通过第二通道传输至解密函数，解密函数根据所述响应输出信号和秘钥进行解密，生成解密后的密文输入信号。本发明实现双通道密文输入信号传输，综合考虑了不确定性和增益受限的问题。
附图说明
[0047]
为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
[0048]
图1为用x
(1)
变量作为驱动的同步系统；
[0049]
图2为本发明实施例双信道混沌保密通信sc原理图；
[0050]
图3为本发明实施例保密通信方法流程图
[0051]
图4为本发明实施例仿真图；
[0052]
图5为本发明实施例秘钥传输示意图；
[0053]
图6为本发明实施例保密通信过程中密文输入信号和解密后密文输入信号示意图。
具体实施方式
[0054]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于
本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0055]
本发明的目的是提供一种增益受限不确定分数阶混沌系统的保密通信方法，以实现同时考虑控制方向未知和增益受限。
[0056]
为使本发明的上述目的、特征和优点能够更加明显易懂，下面结合附图和具体实施方式对本发明作进一步详细的说明。
[0057]
基础知识：
[0058]
1.驱动-响应同步法
[0059]
原理是利用两个非线性动力系中存在着的驱动响应的关系，lyapunov指数为负的稳定部分设置为主系统，再用主系统中驱动信号中的某一信号去驱动响应系统，驱动系统的系统行为决定了响应系统的动态性能表现。该同步方法只需通过信道传送一路加密信号，并且是自同步方式，以一个3维自治动力系统为例，用x
(1)
变量作为驱动变量，采用pc同步的工作原理如图1所示。
[0060]
由图1可以看出，假设对于系统分为稳定部分为和不稳定部分响应系统结构同驱动系统，假设把v
(1)
作为驱动信号，那么响应系统就变为
[0061][0062]
同步理论中的条件lyapunov指数稳定性判据也是这时由pecora和carroll提出的。lyapunov稳定性定理也直接或间接得运用在其他同步控制方法的稳定性证明中，起着至关重要的作用。
[0063]
2.自适应同步法
[0064]
当实际系统中存在不确定因素时，常规的反馈控制方法不再适用，需要系统自动动态调整响应系统的某些参数，此时自适应控制很好的解决了这个问题。现有文献大多是针对特定混沌系统的自适应同步问题，本发明也是基于统一的思想，并没有区别考虑各种混沌系统，而是从不失一般性的系统模型入手，进行控制器的设计。
[0065]
3.滑模变结构同步法
[0066]
滑模控制是本质上来说，是由于其控制系统结构随时间变化而改变，而具有相应的开关特性，滑模面的设计可以由设计者们依情况而定。其特点是对系统的不确定性不敏感，已成为提高系统鲁棒性的重要方法。缺点是变结构控制固有的抖震问题会在一定程度上影响同步的效果，在设计中应尽可能的避免或减小抖震的发生。如何使不确定超混沌系统渐近收敛的问题仍然是未来研究的重点方向之一。
[0067]
4.反演设计法
[0068]
反演的提出始于90年代，是当前控制理论和应用的前沿课题之一，该方法主要是针对不确定严反馈系统，本质是引入虚拟控制律，将系统逐级处理，通过选择合适的lyapunov函数分别逐级证明各闭环子系统的稳定性，最终得到实际控制律，解决了相对复杂的非线性系统的控制问题。不仅可以针对欠驱动系统有很好的效果，而且对于具有严反馈结构的非线性系统的稳定性分析问题和控制器设计难题，也提供了结构化、系统化的解
决方法。而对于非严反馈系统，学者们又提出了交叉严反馈技术，将系统分为多个有共同参数的严反馈系统，本发明正是基于此思想展开研究，期望所设计的同步控制方法能适用于更多的混沌系统。
[0069]
5.神经网络控制
[0070]
神经网络由于其优异的逼近能力，能有效处理未知非线性函数和不确定性，已被应用于混沌控制中，并取得了一些成果
[87]-[89]
。用经典rbf神经网络的对函数进行逼近，优点是权值调节的收敛速度快，无局部极小，分类能力优异且学习速度快。
[0071]
自17世纪始，就有关于分数阶运算的相关记录，然而至今它仍然是一个热门的课题。近二十年来，分数阶微积分(fractional order calculus，简称foc)得到了巨大的关注和发展，它可以很好的描述一些复杂运动、不规则现象、记忆特征、中间过程。分数阶微分方程(fractional differential equations，简称fdes)和常微分方程(ordinary differential equations，简称odes)在描述系统的动态时存在自相似性，并且有大量的分数阶系统普遍存在于自然界和工程实际中。
[0072]
foc实际上是指任意阶次的微积分。下面简单介绍几种常用的定义。
[0073]
定义1.1分数阶积分由riemann-liouville积分定义。函数f(t)的n阶积分(n为正实数)表达式为：
[0074][0075]
其中，为euler's gamma函数。
[0076]
定义1.2单参数mittag-leffler函数，具体公式为：
[0077][0078]
特别的，当α＝1时，式就表示在odes里重要作用的指数函数ez，即
[0079][0080]
双参数(广义)的mittag-leffler函数的表达式为：
[0081][0082]
式中，α＞0，β＞0，z∈c。当β＝1，e
α
(z)＝e
α,1
(z)，进一步有e
1,1
(z)＝ez。
[0083]
广义mittag-leffler函数经过拉普拉斯变换后，在求解fdes的过程中十分重要，其表达式为
[0084][0085]
分数阶算子是非整数阶基本运算的微分和积分运算，其中a和t是运算的起止边界。三种常用的分数阶定义分别为gr
ü
nwald-letnikov型定义、riemann-liouvill型定义和caputo型定义。
[0086]
定义1.3 gr
ü
nwald-letnikov型分数阶导数多用于数值计算，其定义为
[0087][0088]
定义1.4 riemann-liouvill型分数阶导数定义为
[0089][0090]
riemann-liouvill型分数阶导数有超奇异性，20世纪60年代，意大利的caputo提出了弱奇异的分数阶微分定义。
[0091]
定义1.5 caputo分数阶导数定义为
[0092][0093]
比较定义1.4和定义1.5来看，二者主要差别在于微积分顺序不同，即对函数f(t)的要求不同，定义1.5对f(t)要求是n阶可微。
[0094]
由foc的定义可以看出，输入函数的初值以衰减的形式进入输出，零初值下foc是卷积分的形式。因此，foc实际上是一个积分，且随时间衰减记忆，这就是分数阶微分算子最大的特点。
[0095]
稳定性是设计控制器时首要考虑的问题，是系统工作的前提。lyapunov技术不仅可以用来分析ode的稳定性，也可以分析非线性系统稳定性的基本工具，2011年j.c.trigeassou等定义了一种频率分布模型，是目前能够与伪状态变量完全等价的一种定义方式。本发明对分数阶系统的研究则是以此理论为基础展开。
[0096]
混沌在保密通信(secure communication，简称sc)中的应用打实了基础。虽然目前应用更多的是伪随机信号加密，但是混沌加密作为一种动态加密，不仅在处理速度上不依赖于密钥长度，计算效率高，既可以用于视频、语音等实时信号处理，又可以满足图像、军事命令、资料文件等静态加密的需求。复杂混沌系统加密的信息破译难度很大，因此混沌加密在sc中的应用一直以来都是研究的热点问题。
[0097]
如图2-3所示，本发明公开一种增益受限不确定分数阶混沌系统的保密通信方法，具体包括：
[0098]
步骤s1：构建分数阶混沌驱动系统。
[0099]
步骤s2：构建分数阶混沌响应系统。
[0100]
步骤s3：根据所述分数阶混沌驱动系统和所述分数阶混沌响应系统构建分数阶误差。
[0101]
步骤s4：构建控制方向未知和增益受限的边界条件。
[0102]
步骤s5：基于所述边界条件构建增益受限的nussbaum增益控制器。
[0103]
步骤s6：密文输入信号同步数据传输；传输密文输入信号时，分数阶混沌驱动系统输出混沌驱动输入信号，并通过第一通道传输所述混沌驱动输入信号，所述混沌驱动输入信号经过nussbaum增益控制器和分数阶混沌响应系统后生成响应输出信号，加密函数利用所述混沌驱动输入信号对密文输入信号进行掩盖后生成秘钥，并通过第二通道传输至解密函数，解密函数根据所述响应输出信号和秘钥进行解密，生成解密后的密文输入信号。
[0104]
下面对各个步骤进行详细论述：
[0105]
步骤s1：构建分数阶混沌驱动系统，具体公式为：
[0106]dα
x＝f(x)θ
x
f(x)
ꢀꢀ
(1)；
[0107]
其中，d
α
x表示分数阶导数，f(x)∈rn×m为系统函数矩阵，θ
x
∈rm为驱动系统的实际值，f(x)∈rn为已知或未知的非线性函数向量(函数矩阵)，x为系统的混沌驱动输入信号，x为x(t)的简写。
[0108]
步骤s2：构建分数阶混沌响应系统，具体公式为：
[0109]dα
y＝g(y)θy g(y) bu
ꢀꢀ
(2)；
[0110]
其中，y∈rn为系统的响应输出信号，g(y)∈rn×m为函数矩阵，θy∈rm为响应系统的实际值，g(y)∈rn为已知或未知的非线性函数向量，b为未知控制系数，u为控制输入，d
α
y为分数阶导数。
[0111]
步骤s3：根据所述分数阶混沌驱动系统和所述分数阶混沌响应系统构建分数阶误差，具体公式为：
[0112][0113]
其中，e为误差向量，y∈rn为系统的响应输出信号，g(y)∈rn×m为函数矩阵，θ
x
∈rm为驱动系统的实际值，θy∈rm为响应系统的实际值，θ
x
∈rm和θy∈rm均为未知的参数向量，g(y)∈rn为已知或未知的非线性函数向量，b为未知控制系数，u为控制输入，f(x)∈rn×m为系统函数矩阵，f(x)为已知或未知的非线性函数向量，x为系统的混沌驱动输入信号。
[0114]
控制目的是使得当t
→
∞时，||e||
→
0，即实现响应系统与驱动系统实现同步。
[0115]
步骤s4：构建控制方向未知和增益受限的边界条件，具体包括：
[0116]
1、控制增益k受限，满足|k|≤k
sat
，k
sat
为系统对增益界的限制要求。
[0117]
2、k
sat
足够大，能够满足系统稳定的能量要求。
[0118]
3、控制方向b未知有界，且b的界已知，即满足||b||
∞
≤b
max
，其中b
max
为控制方向边界值，正常数，b的元素在未知闭区间i＝[l
‑ l

]中取值，且l-、l

分别为未知闭区间的下限和上限。
[0119]
步骤s5：基于所述边界条件构建增益受限的nussbaum增益控制器，具体公式为：
[0120][0121]
其中，为驱动系统的估计值，为响应系统的估计值，θ
x
为驱动系统的实际值，θy为的响应系统的实际值，s为分数阶积分滑模曲面，u为控制输入，f(x)为系统函数矩阵，f(x)为已知或未知的非线性函数向量，g(y)为函数矩阵，g(y)为已知或未知的非线性函数向量，e为误差向量，r1、r2均为滑模系数，s为分数阶积分滑模曲面，n(k)为nussbaum函数，k为
nussbaum增益，为nussbaum增益的调节律，h为增益边界，l为nussbaum增益的调节律变量，c为系数矩阵，ud为控制率。
[0122]
步骤s7：验证nussbaum增益控制器的增益受限，具体步骤包括：
[0123]
步骤s71：构建分数阶积分滑模曲面，具体公式为：
[0124]
s＝e(t) ci
α
e(t)
ꢀꢀ
(5)；
[0125]
其中，s为分数阶积分滑模曲面，s∈rn，c＝diag(c1,c2,
…
,cn)∈rn×n，ci＞0，(i＝1,2,...,n)，ci为常数，e(t)为误差，i
α
为分数阶系数，n为自然数。
[0126]
步骤s72：基于线性频率分布模型确定滑模面的等价频率分布模型，具体公式为：
[0127][0128]
其中，μ(ω)为权重函数，μ(ω)＝sin(απ)/πω
α
，z(ω,t)∈r为实际误差变量，ω为频率模型变量，d
α
s为分数阶滑模面，α为分数，s为分数阶积分滑模曲面。
[0129]
步骤s73：基于滑模面的等价频率分布模型构建第一lyapunov函数的导数，具体公式为：
[0130][0131]
其中，g(y)为响应系统函数矩阵，θ
x
、θy均为响应系统的实际值，g(y)为已知或未知的非线性函数向量，f(x)为系统函数矩阵，f(x)为已知或未知的非线性函数向量，b为未知控制系数，u为控制输入，c为系数矩阵，e为误差，μ(ω)为权重函数，μ(ω)＝sin(απ)/πω
α
，z(ω,t)∈r为实际误差变量，ω为频率模型变量，d
α
s为分数阶滑模面，α为分数，s为分数阶积分滑模曲面。
[0132]
步骤s74：利用所述nussbaum增益控制器对所述第一lyapunov函数的导数进行化简，获得化第一简化导数，具体公式为：
[0133]
[0134]
其中，为第一简化导数，为驱动系统的实际值θ
x
与驱动系统的估计值之间的差值，为响应系统的实际值θy与响应系统的估计值之间的差值，s为分数阶积分滑模曲面，r1、r2均为滑模系数，f(x)为系统函数矩阵，g(y)为响应系统函数矩阵，n(k)为nussbaum函数，k为nussbaum增益，b为未知控制系数，为nussbaum增益的调节律，μ(ω)为权重函数，z(ω,t)∈r为实际误差变量，ω为频率分布模型中的变量。
[0135]
步骤s75：基于自适应律分别构建驱动系统的频率分布模型和响应系统的频率分布模型；所述自适应律的具体公式为：
[0136][0137]
其中，和分别为估计误差的分数阶形式，s为分数阶积分滑模曲面，f(x)为系统函数矩阵，g(y)为响应系统函数矩阵。
[0138]
驱动系统的频率分布模型的具体公式为：
[0139][0140]
其中，ω为频率分布模型中的变量，为函数，为估计误差的分数阶形式，为差值，μ(ω)为权重函数。
[0141]
响应系统的频率分布模型的具体公式为：
[0142][0143]
其中，ω为频率分布模型中的变量，为函数，为估计误差的分数阶形式，为差值，μ(ω)为权重函数。
[0144]
步骤s76：基于所述驱动系统的频率分布模型和所述响应系统的频率分布模型构建第二lyapunov函数的导数，具体公式为：
[0145][0146]
其中，为第二lyapunov函数的导数，ω为频率分布模型中的变量，μ(ω)为权重函数，均为函数，均为估计误差的分数阶形式，为驱动系统的实际值θ
x
与驱动系统的估计值之间的差值，为响应系统的实际值θy与响应系统的估计值之间的差值，f(x)为系统函数矩阵，g(y)为响应系统函数矩阵，f(x)为系统函数矩阵，s为分数阶积分滑模曲面。
[0147]
步骤s77：将所述第一简化导数和所述第二lyapunov函数的导数进行求和简化，获得第二简化导数，具体公式为：
[0148][0149]
其中，为第二简化导数，分别为的简写，为第一简化导数，为第二lyapunov函数的导数，为驱动系统的实际值θ
x
与驱动系统的估计值之间的差值，为响应系统的实际值θy与响应系统的估计值之间的差值，s为分数阶积分滑模曲面，r1、r2均为滑模系数，f(x)为系统函数矩阵，g(y)为响应系统函数矩阵，n(k)为nussbaum函数，k为nussbaum增益，b为未知控制系数，为nussbaum增益的调节律，μ(ω)为权重函数，z(ω,t)∈r为实际误差变量，ω为频率分布模型中的变量。
[0150]
步骤s78：将所述第二简化导数进一步简化，获得第三简化导数，具体公式为：
[0151][0152]
其中，为第二简化导数，k为nussbaum增益，b为未知控制系数，为nussbaum增益的调节律，n(k)为nussbaum函数。
[0153]
步骤s79：对所述第三简化导数两边积分，获得积分公式，具体公式为：
[0154][0155]
其中，v(t)为第三简化导数的积分函数，v(0)为t＝0时的函数值，k为nussbaum增益，l(t)为t时刻的函数值，l(0)为t＝0时的函数值，n(k)为nussbaum函数，b为未知控制系
数。
[0156]
通过上述论证可知，构建公式(7)、(12)和(13)是为了证明驱动系统、响应系统以及滑膜曲面均是稳定性的。由公式(15)可知，因为导值小于一个数，所以认为系统渐近。
[0157]
本发明公开定义了分数阶积分型滑模面，利用等价频率分布模型定义lyapunov函数，证明了同步误差系统的稳定性；利用nussbaum函数不仅处理了控制方向未知的问题，也处理了由输入饱和引起的非线性现象，结合了反演技术、神经网络技术，实现了不确定混沌系统的保密通信同步，最后数值仿真验证了所设计方法的有效性和可行性。
[0158]
仿真分析：
[0159]
为了验证所设计的增益受限nussbaum增益控制的有效性，本文以分数阶chen混沌系统作为驱动系统
[0160][0161]
构建带控制输入的分数阶系统作为响应系统
[0162][0163]
式中βi∈(0,1)；ui为控制量；bi为控制系数。
[0164]
本发明设置a
x
，b
x
，c
x
，ay，by，cy均为未知参量；αi＝βi＝0.9；驱动系统和响应系统的初始值分别为(x1,x2,x3)＝(1,2,-1)和(y1,y2,y3)＝(2,-1,1)；参数估计的初值nussbaum增益的初始值li(0)＝0.1，未知控制系数仿真结果如下图4所示,(a)为误差e1曲线，(b)为误差e2曲线，(c)为误差e3曲线，(d)为参数a
x
曲线，(e)为参数b
x
曲线，(f)为参数c
x
曲线，(g)为参数ay曲线，(h)为参数by曲线，(i)为参数cy曲线，(j)为nussbaum增益k1曲线，(k)为nussbaum增益l1曲线，(l)为nussbaum增益k2曲线，(m)为nussbaum增益l2曲线，(n)为nussbaum增益k3曲线，(o)为nussbaum增益l3曲线，(p)为控制量u1曲线，(q)为控制量u2曲线，(r)为控制量u3曲线。
[0165]
从图4中可以看到，在t＝4s时，未知控制系数b突变，驱动系统和响应系统能迅速同步，各参数进行了相应的调节，三个状态变量的同步误差快速趋于0，并且将nussbaum增益控制到一定范围内(k，l的曲线达到最大值，没有一直增加)，说明采用本发明所设计的滑模自适应nussbaum增益控制很好的实现了参数不确定、控制方向不确定在增益受限情况下的分数阶混沌系统同步。在理论上实现了对控制增益的限制，使分数阶混沌同步控制中的高增益问题得到了一定程度的解决。
[0166]
将上述方法应用到保密通信中，如图2所示，传输密文输入信号m(t)时，分数阶混沌驱动系统输出混沌驱动输入信号x(t)，并通过第一通道传输所述混沌驱动输入信号x
(t)，所述混沌驱动输入信号x(t)经过控制器和分数阶混沌响应系统后生成响应输出信号y(t)，加密函数利用所述混沌驱动输入信号x(t)对密文输入信号m(t)进行掩盖后生成秘钥p(t)，并通过第二通道传输至解密函数，解密函数根据所述响应输出信号和秘钥p(t)进行解密，生成解密后的密文输入信号
[0167]
本实施例中，输密文输入信号：m(t)＝sin(0.5t) 0.5sin(t)，如图6所示。
[0168]
秘钥p(t)：如图5所示。
[0169]
解密后的密文输入信号如图6所示。
[0170]
由图6可以看出，在双通道保密通信过程中，m(t)与完全重合，说明输入同步输出。
[0171]
本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。
[0172]
本发明中应用了具体个例对本发明的原理及实施方式进行了阐述，以上实施例的说明只是用于帮助理解本发明的方法及其核心思想；同时，对于本领域的一般技术人员，依据本发明的思想，在具体实施方式及应用范围上均会有改变之处。综上所述，本说明书内容不应理解为对本发明的限制。