一种行星滚柱丝杠副的不确定性分析方法及系统

1.本发明涉及行星滚柱丝杠精密螺纹传动技术领域，特别涉及一种行星滚柱丝杠副的不确定性分析方法及系统。


背景技术：

2.行星滚柱丝杠副是一种精密螺纹传动装置，主要用作机电作动器的执行机构。通常，丝杠连接伺服电机，螺母连接负载，多个滚柱在丝杠与螺母之间做行星运动。通过滚柱两侧的螺纹同时与丝杠和螺母啮合，能够将丝杠的旋转运动转化为螺母的线型推力。由于行星滚柱丝杠副具有大量的接触点且没有滚动体循环装置，从而具有高承载能力、良好的鲁棒性、速度和加速度快等优点。
3.在行星滚柱丝杠副制造、装配、测量和操作等过程中广泛存在的不确定性，这些不确定性因素可能加剧载荷分布不均程度，导致螺纹即使在额定负载范围内也可能出现过接触应力，同一批次产品在相同工况下具有不同的使用寿命。因此，考虑不确定性的多螺纹副的载荷分布和接触特性会极大地影响行星滚柱丝杠副的耐用性和可靠性。
4.不确定性分析常被用作衡量产品质量的评价标准，被视为设计过程的必要环节。但目前还缺乏一个合理有效的不确定性分析模型来初步评估行星滚柱丝杠副的可靠性。对行星滚柱丝杠副进行不确定性分析有助于设计者在选择产品的材料之前找到影响其失效的主要因素，从而提出防止或推迟失效的措施，为行星滚柱丝杠副的设计优化提供理论依据，对实现国产化高性能行星滚柱丝杠副的研制和提升机电伺服作动系统的综合性能有着重要的理论意义和工程应用价值。


技术实现要素：

5.本发明要解决的技术问题是提供一种合理有效的行星滚柱丝杠副的不确定性分析方法。
6.为了解决上述问题，本发明提供了一种行星滚柱丝杠副的不确定性分析方法，所述行星滚柱丝杠副的不确定性分析方法包括以下步骤：
7.s1、通过结构参数、材料性能及边界条件求解行星滚柱丝杠副螺纹牙载荷分布和接触特性，考虑结构参数、材料性能及边界条件中存在的不确定性，基于s-n曲线和应力-强度干涉理论构建行星滚柱丝杠副螺纹牙接触疲劳失效模式下的极限状态函数；
8.s2、引入确定性的低偏差点集halton序列，采用试验设计方法分析不确定性因素对行星滚柱丝杠副螺纹牙承载能力及接触性能影响的敏感性和贡献程度，将重要度排序靠前的参数作为随机变量来降低极限状态功能函数的维数，得到简化后的极限状态函数；
9.s3、引入期望风险学习函数构建行星滚柱丝杠副主动学习代理模型，采用拟蒙特卡洛方法产生抽样样本点，调用所建立的主动学习代理模型计算每组样本点对应的简化后的极限状态函数，对行星滚柱丝杠副进行不确定性分析，得到行星滚柱丝杠副在任一工况下的失效概率及可靠性灵敏度。
10.作为本发明的进一步改进，步骤s1中，通过结构参数、材料性能及边界条件求解行星滚柱丝杠副螺纹牙载荷分布和接触特性，包括：
11.采用迭代算法求解行星滚柱丝杠副螺纹牙载荷分布模型，如下：
[0012][0013]
其中，ps,pr和pn分别为丝杠、滚柱和螺母的螺距，τ为滚柱参与接触的螺纹牙数，z为滚柱个数，螺纹从丝杠固定端到自由端依次编号，i＝1,2,
…
,τ，f 为轴向外载荷，f
sri
为滚柱与丝杠接触侧第i对螺纹牙上承受的轴向载荷，f
nri
为滚柱与螺母接触侧第i对螺纹牙上承受的轴向载荷；为丝杠轴段刚度，为滚柱轴段刚度，为螺母轴段刚度，为丝杠螺纹牙刚度，为滚柱螺纹牙刚度，为螺母螺纹牙刚度；
[0014]
求解丝杠与滚柱的接触刚度，如下：
[0015][0016]
其中，为丝杠与滚柱的接触刚度；为丝杠与滚柱第i对螺纹牙的弹性接触变形；
[0017]
求解螺母与滚柱螺纹副接触刚度，如下：
[0018][0019]
其中，为螺母与滚柱螺纹副接触刚度，为螺母与滚柱第i对螺纹牙的弹性接触变形。
[0020]
作为本发明的进一步改进，丝杠与滚柱第i对螺纹牙的弹性接触变形的计算公式如下：
[0021][0022][0023]
其中，k(e)和l(e)是第一类和第二类完全椭圆积分，a为接触椭圆的长半轴， b为接触椭圆的短半轴，为接触椭圆的偏心率，ke＝b/a，为等效弹性模量，es和vs为丝杠的弹性模量和泊松比，er和vr为滚柱的弹性模量和泊松比，和λ为接触角和滚柱的螺旋升角。
[0024]
作为本发明的进一步改进，基于s-n曲线和应力-强度干涉理论构建行星滚柱丝杠副螺纹牙接触疲劳失效模式下的极限状态函数，如下：
[0025][0026][0027][0028]
其中，x＝(x1,x2,
…
xi…
,xn)为影响极限状态函数的随机变量，xi为第i个随机变量，n为随机变量个数，σ
hlim
为接触疲劳极限，σ
sri
为丝杠与滚柱第i对螺纹牙上的接触应力，为滚柱与丝杠接触侧上所有螺纹牙之间的最大接触应力，σ
nri
为螺母与滚柱第i对螺纹牙上的接触应力，为滚柱与螺母接触侧上所有螺纹牙之间的最大接触应力；f
sri
为滚柱与丝杠接触侧第i对螺纹牙上承受的轴向载荷，f
nri
为滚柱与螺母接触侧第i对螺纹牙上承受的轴向载荷；a为接触椭圆的长半轴，b为接触椭圆的短半轴，和λ为接触角和滚柱的螺旋升角。
[0029]
作为本发明的进一步改进，步骤s2包括：
[0030]
s21、对于行星滚柱丝杠副的每个随机变量xi在[0,1]的区间内生成halton 序列，由halton序列得到输入参数矩阵为x＝(x1,x2,
…
,xi,
…
,xn)，其中 xi＝(x
i1
,x
i2
,
…
,x
ij
,
…
,x
in
)
t
为xi的样本向量；
[0031]
s22、响应量包括：滚柱两接触侧的最大载荷分布系数：最大接触应力和螺纹副上的局部接触应力σ
sri
,σ
nri
，通过计算得到响应矩阵为： y＝(y1,y2,
…
,yk,
…
,ym)，其中yk＝(y
k1
,y
k2
,
…
,y
kj
,
…
,y
kn
)
t
为第k个响应yk的样本向量；
[0032]
s23、将矩阵x和y中的数据在[-1,1]范围内进行归一化，再用多项式响应面法将这些数据进行拟合：
[0033]
s24、将多项式系数以百分比的形式来表示，可以反映每个输入参数对第k个响应量的影响程度；
[0034]
s25、选择重要度排序靠前的参数来降低随机变量的维数，得到简化的行星滚柱丝杠副的极限状态函数。可选地，选择排名前五的参数。
[0035]
作为本发明的进一步改进，步骤s3中包括：
[0036]
s31、在不确定域中随机生成n0＝20个样本，计算简化后的极限状态功能函数值，引入期望风险学习函数构建行星滚柱丝杠副主动学习代理模型，首先构造初始的代理模型，如下：
[0037]
[0038][0039]
u＝f
t
r-1
r-f(x)
[0040]
其中，y＝[g(x1),g(x2),
…
,g(xn)]
t
为具有n个样本点的真实响应函数， f(x)＝[f1(x),f2(x),
…fi
(x),
…
,f
p
(x)]
t
为回归多项式基函数向量，β＝[β1,β2,
…
βi,
…
,β
p
]
t
为回归系数向量，p为回归多项式的个数，r为待测点与样本点之间的相关向量函数，f＝[f(x1)
t
,f(x2)
t
,
…
,f(xn)
t
]
t
为n
×
p阶扩展矩阵，r为n
×
n阶对称正定相关矩阵，为近似极限状态函数g(x)的估计值，为的方差，g(x)计算如下：
[0041][0042]
其中，z(x)为服从n(0,σ2)正态分布的随机过程，则任意两个样本点w和x 之间的协方差为：
[0043]
cov[z(w),z(x)]＝σ2r(θ,w,x)
[0044]
其中，θ＝[θ1,θ2,
…
,θn]
t
为相关性参数，r(θ,w,x)为表示变量θ,w,x相关性的函数且可以利用连续可微的高斯相关性函数来描述为：
[0045][0046]
其中，回归系数β及方差σ2可以用广义最小二乘回归方法表示为：
[0047]
β＝(f
t
r-1
f)-1ft
r-1y[0048][0049]
s32、在不确定性域中生成nc＝105个候选样本；
[0050]
s33、根据初始代理模型计算nc个样本点的估计值和期望风险的估计值取erf值最大的点为训练点x*，计算方法如下：
[0051][0052]
其中，sign(x)为符号函数，当x＞0时，sign(x)＝1，当x＜0时，sign(x)＝-1，φ()为标准正态分布的概率密度函数，ψ()为标准正态分布的累积分布函数；
[0053]
s34、设置阈值或收敛条件为ε＝10-5
；如果max(erf)》ε，增加x*作为新的训练点，更新行星滚柱丝杠副主动学习代理模型；
[0054]
s35、重复步骤s33～s35，直到max(erf)≤ε；
[0055]
s36、利用更新后的星滚柱丝杠副主动学习代理模型，采用拟蒙特卡洛方法产生抽样样本点，调用所建立的主动学习代理模型计算每组样本点对应的简化后的极限状态函数，对行星滚柱丝杠副进行不确定性分析，得到行星滚柱丝杠副在任一工况下的失效概率及可靠性灵敏度。
[0056]
作为本发明的进一步改进，所述采用拟蒙特卡洛方法产生抽样样本点，调用所建立的主动学习代理模型计算每组样本点对应的简化后的极限状态函数，对行星滚柱丝杠副
进行不确定性分析，得到行星滚柱丝杠副在任一工况下的失效概率及可靠性灵敏度，包括：
[0057]
s361、对于行星滚柱丝杠副的每个随机变量xi在[0,1]的区间内生成halton 序列，各变量相互独立且均为正态分布，随机变量的累积概率分布函数f(x
ij
) 可表示为：
[0058][0059]
其中，x
ij
为第i个随机变量的第j个样本值，f(xi)为随机变量xi的概率密度函数，n为抽样样本数，为第x
ij
对应的halton数，其中halton序列的具体生成过程为：
[0060]
若q为任意质数，则任意自然数j有唯一的q进制表达式：
[0061]
j＝j0 j1q j2q2
···
jkqk[0062][0063]ji
∈{0,1,
···
,q-1}；i＝0,1,
···
,k
[0064]
其中，k表示lnj/lnq的整数部分，以q为底的基逆函数定义为：
[0065][0066]
对于任意自然数j＞0，均满足若前n个质数为q1,q2,
…
,qn，则 n维halton序列可以表示为：
[0067][0068]
s362、获得随机变量x
ij
的样本值
[0069]
s363、获得许用接触应力的样本点
[0070]
s364、计算每组随机向量的样本xj＝(x
1j
,x
2j
,
…
,x
nj
)
t
作用下的载荷分布和局部接触特性，得到滚柱与丝杠或螺母接触侧上的最大接触应力，然后进一步计算极限状态函数g(xj)，如果g(xj)≤0，状态指示函数if(xj)＝1，否则if(xj)＝0；
[0071]
s365、失效概率的估计及其变异系数计算如下：
[0072][0073][0074]
其中，nf为失效样本数；
[0075]
s366、可靠性灵敏度的估计值如下：
[0076][0077]
其中，f
x
(x)为随机变量的联合概率密度函数，为基本随机变量xi的第k 个分
布参数，mi为第i个随机变量xi的分布参数的数量，正态分布随机变量具有均值和标准差两个分布参数，可靠性灵敏度可以计算为：
[0078][0079]
本发明还提供了一种计算机可读存储介质，所述存储介质包括存储的程序，其中，所述程序执行上述任意一项所述的行星滚柱丝杠副的不确定性分析方法。
[0080]
本发明还提供了一种电子设备，其包括：一个或多个处理器，存储器以及一个或多个程序，其中，所述一个或多个程序被存储在所述存储器中，并且被配置为由所述一个或多个处理器执行，所述一个或多个程序包括用于执行上述任意一项所述的行星滚柱丝杠副的不确定性分析方法。
[0081]
本发明还提供了一种行星滚柱丝杠副的不确定性分析系统，其包括以下模块：
[0082]
极限状态函数构建模块，用于通过结构参数、材料性能及边界条件求解行星滚柱丝杠副螺纹牙载荷分布和接触特性，考虑结构参数、材料性能及边界条件中存在的不确定性，基于s-n曲线和应力-强度干涉理论构建行星滚柱丝杠副螺纹牙接触疲劳失效模式下的极限状态函数；
[0083]
极限状态函数简化模块，用于引入确定性的低偏差点集halton序列，采用试验设计方法分析不确定性因素对行星滚柱丝杠副螺纹牙承载能力及接触性能影响的敏感性和贡献程度，将重要度排序靠前的参数作为随机变量来降低极限状态功能函数的维数，得到简化后的极限状态函数；
[0084]
不确定性分析模块，用于引入期望风险学习函数构建行星滚柱丝杠副主动学习代理模型，采用拟蒙特卡洛方法产生抽样样本点，调用所建立的主动学习代理模型计算每组样本点对应的简化后的极限状态函数，对行星滚柱丝杠副进行不确定性分析，得到行星滚柱丝杠副在任一工况下的失效概率及可靠性灵敏度。
[0085]
本发明的有益效果：
[0086]
本发明通过构建行星滚柱丝杠副螺纹牙接触疲劳失效模式下的极限状态函数，将极限状态函数简化，并引入期望风险学习函数构建行星滚柱丝杠副主动学习代理模型，采用拟蒙特卡洛方法产生抽样样本点，调用所建立的主动学习代理模型计算每组样本点对应的简化后的极限状态函数，对行星滚柱丝杠副进行不确定性分析，得到行星滚柱丝杠副在任一工况下的失效概率及可靠性灵敏度。可以有效减少极限状态函数功能函数调用次数，降低计算成本，提高行星滚柱丝杠副的不确定性分析效率，帮助设计者找出影响结构可靠
性的主要因素，进而为产品的设计优化奠定理论基础。
[0087]
上述说明仅是本发明技术方案的概述，为了能够更清楚了解本发明的技术手段，而可依照说明书的内容予以实施，并且为了让本发明的上述和其他目的、特征和优点能够更明显易懂，以下特举较佳实施例，并配合附图，详细说明如下。
附图说明
[0088]
图1是本发明实施例中行星滚柱丝杠副的不确定性分析方法的整体流程图；
[0089]
图2为本发明实施例中行星滚柱丝杠副的结构示意图；
[0090]
图3为本发明实施例中行星滚柱丝杠副的不确定性分析方法的计算流程图；
[0091]
图4为本发明实施例中不确定性因素对行星滚柱丝杠副承载特性与接触性能的重要度排序图；
[0092]
图5为本发明实施例中采用蒙特卡洛方法和拟蒙特卡洛方法估算行星滚柱丝杠副失效概率的收敛速度和计算时间的对比图；
[0093]
图6为本发明实施例中行星滚柱丝杠副极限状态函数的三维网格曲面图；
[0094]
图7为本发明实施例中行星滚柱丝杠副在不同工况下的极限状态函数的三维网格曲面图。
[0095]
标记说明：1、丝杠；2、滚柱；3、螺母；4、内齿圈；5、行星架；6、弹性挡圈。
具体实施方式
[0096]
下面结合附图和具体实施例对本发明作进一步说明，以使本领域的技术人员可以更好地理解本发明并能予以实施，但所举实施例不作为对本发明的限定。
[0097]
如图1所示，为本发明优选实施例中的行星滚柱丝杠副的不确定性分析方法，该行星滚柱丝杠副的不确定性分析方法包括以下步骤：
[0098]
步骤s1、通过结构参数、材料性能及边界条件求解行星滚柱丝杠副螺纹牙载荷分布和接触特性，考虑结构参数、材料性能及边界条件中存在的不确定性，基于s-n曲线和应力-强度干涉理论构建行星滚柱丝杠副螺纹牙接触疲劳失效模式下的极限状态函数；
[0099]
如图2所示，常见的行星滚柱丝杠副结构包括：一个丝杠1、一个螺母3、多个滚柱2、一对行星架5、一对内齿圈4和一对弹性挡圈6等；
[0100]
所述内齿圈4安装在螺母3两端，所述行星架5安装在所述内齿圈4内，所述多个滚柱2通过所述行星架5均匀分布在丝杠1与螺母3之间，所述滚柱 2两端带有直齿分别与所述内齿圈4啮合，所述丝杠1为多头梯形外螺纹，所述螺母3为多头梯形内螺纹，所述丝杠1与所述螺母3具有相同的螺纹头数，所述滚柱2为单头外螺纹，所述滚柱牙型轮廓为弧形且圆心位于滚柱轴线上，所述丝杠1与螺母3分别与所述滚柱2两侧的螺纹牙接触共同参与承载，所述滚柱2、丝杠1和螺母3的轴线平行，所述滚柱2既绕自身轴线自转又绕所述丝杠1轴线公转，所述滚柱2与所述螺母3保持相同速度轴向位移，所述螺母 3无圆周运动。
[0101]
在其中一实施例中，步骤s1具体包括：
[0102]
采用迭代算法求解行星滚柱丝杠副螺纹牙载荷分布模型，如下：
[0103][0104]
其中，ps,pr和pn分别为丝杠、滚柱和螺母的螺距，τ为滚柱参与接触的螺纹牙数，z为滚柱个数，螺纹从丝杠固定端到自由端依次编号，i＝1,2,
…
,τ，f 为轴向外载荷，f
sri
为滚柱与丝杠接触侧第i对螺纹牙上承受的轴向载荷，f
nri
为滚柱与螺母接触侧第i对螺纹牙上承受的轴向载荷；为丝杠轴段刚度，为滚柱轴段刚度，为螺母轴段刚度，为丝杠螺纹牙刚度，为滚柱螺纹牙刚度，为螺母螺纹牙刚度；
[0105]
为丝杠轴段刚度，为滚柱轴段刚度，为螺母轴段刚度，es,er和en分别为丝杠、滚柱和螺母的材料的弹性模量，as, ar和an分别为丝杠、滚柱和螺母的最小横截面积。
[0106]
为丝杠螺纹牙刚度，为丝杠第i个螺纹牙的变形，包括弯曲变形剪切变形牙根倾斜变形牙根剪切变形和径向收缩变形具体计算如下：
[0107][0108]
其中，vs,hs,βs,ds,和cs分别表示丝杠的泊松比、螺纹牙厚、牙侧角、螺纹中径、螺纹根宽和螺纹顶宽。
[0109]
为滚柱螺纹牙刚度，在与丝杠接触侧，为
滚柱第i个螺纹牙的变形，包括弯曲变形剪切变形牙根倾斜变形牙根剪切变形和径向收缩变形具体计算如下：
[0110][0111]
其中，vr,hr,βr,dr,和cr分别表示滚柱的泊松比、螺纹牙厚、牙侧角、螺纹中径、螺纹根宽和螺纹顶宽。在滚柱与螺母接触侧，滚柱螺纹牙刚度计算方法相同，只需将上式f
sri
换成f
nri
。
[0112]
为螺母螺纹牙刚度，为螺母的第i个螺纹牙的变形，包括弯曲变形剪切变形牙根倾斜变形牙根剪切变形和径向膨胀变形具体计算如下：
[0113][0114]
其中，vn,hn,βn,dn,和cn分别表示螺母的泊松比、螺纹牙厚、牙侧角、螺纹中径、螺纹根宽和螺纹顶宽。
[0115]
下面计算：为丝杠与滚柱的接触刚度，为丝杠与滚柱第i 对螺纹牙的弹性接触变形，具体计算如下：
[0116][0117][0118]
其中，k(e)和l(e)是第一类和第二类完全椭圆积分，a为接触椭圆的长半轴， b为接触椭圆的短半轴，为接触椭圆的偏心率，ke＝b/a，为等效弹性模量，es和vs为丝杠的弹性模量和泊松比，er和vr为滚柱的弹性模量和泊松比，和λ为接触角和滚柱的螺旋升角。
[0119]
为螺母与滚柱螺纹副接触刚度，为螺母与滚柱第i对螺纹牙的弹性接触变形，与计算方法相同，在此不多赘述。
[0120]
基于s-n曲线和应力-强度干涉理论构建行星滚柱丝杠副螺纹牙接触疲劳失效模式下的极限状态函数，如下：
[0121]
[0122][0123][0124]
其中，x＝(x1,x2,
…
xi…
,xn)为影响极限状态函数的随机变量，xi为第i个随机变量，n为随机变量个数，σ
hlim
为接触疲劳极限，σ
sri
为丝杠与滚柱第i对螺纹牙上的接触应力，为滚柱与丝杠接触侧上所有螺纹牙之间的最大接触应力，σ
nri
为螺母与滚柱第i对螺纹牙上的接触应力，为滚柱与螺母接触侧上所有螺纹牙之间的最大接触应力。
[0125]
步骤s2、引入确定性的低偏差点集halton序列，采用试验设计方法分析不确定性因素对行星滚柱丝杠副螺纹牙承载能力及接触性能影响的敏感性和贡献程度，将重要度排序靠前的参数作为随机变量来降低极限状态功能函数的维数，得到简化后的极限状态函数；
[0126]
在其中一实施例中，步骤s2具体包括：
[0127]
步骤s21、对于行星滚柱丝杠副的每个随机变量xi在[0,1]的区间内生成 halton序列，由halton序列得到输入参数矩阵为x＝(x1,x2,
…
,xi,
…
,xn)，其中 xi＝(x
i1
,x
i2
,
…
,x
ij
,
…
,x
in
)
t
为xi的样本向量；
[0128]
步骤s22、响应量包括：滚柱两接触侧的最大载荷分布系数：最大接触应力和螺纹副上的局部接触应力σ
sri
,σ
nri
，通过计算得到响应矩阵为： y＝(y1,y2,
…
,yk,
…
,ym)，其中yk＝(y
k1
,y
k2
,
…
,y
kj
,
…
,y
kn
)
t
为第k个响应yk的样本向量；
[0129]
步骤s23、将矩阵x和y中的数据在[-1,1]范围内进行归一化，再用多项式响应面法将这些数据进行拟合：
[0130]
步骤s24、将多项式系数以百分比的形式来表示，可以反映每个输入参数对第k个响应量的影响程度；
[0131]
步骤s25、选择重要度排序靠前的参数来降低随机变量的维数，得到简化的行星滚柱丝杠副的极限状态函数。
[0132]
步骤s3、引入期望风险学习函数构建行星滚柱丝杠副主动学习kriging (active learning kriging,alk)代理模型，采用拟蒙特卡洛方法(quasi-montecarlo,qmc)产生抽样样本点，调用所建立的主动学习代理模型计算每组样本点对应的简化后的极限状态函数，对行星滚柱丝杠副进行不确定性分析，得到行星滚柱丝杠副在任一工况下的失效概率及可靠性灵敏度。
[0133]
参照图3，在其中一实施例中，步骤s3具体包括：
[0134]
s31、在不确定域中随机生成n0＝20个样本，计算简化后的极限状态功能函数值，引入期望风险学习函数构建行星滚柱丝杠副主动学习代理模型，首先构造初始的代理模型，如下：
[0135]
[0136][0137]
u＝f
t
r-1
r-f(x)
[0138]
其中，y＝[g(x1),g(x2),
…
,g(xn)]
t
为具有n个样本点的真实响应函数， f(x)＝[f1(x),f2(x),
…fi
(x),
…
,f
p
(x)]
t
为回归多项式基函数向量，β＝[β1,β2,
…
βi,
…
,β
p
]
t
为回归系数向量，p为回归多项式的个数，r为待测点与样本点之间的相关向量函数，f＝[f(x1)
t
,f(x2)
t
,
…
,f(xn)
t
]
t
为n
×
p阶扩展矩阵，r为n
×
n阶对称正定相关矩阵，为近似极限状态函数g(x)的估计值，为的方差，g(x)计算如下：
[0139][0140]
其中，z(x)为服从n(0,σ2)正态分布的随机过程，则任意两个样本点w和x 之间的协方差为：
[0141]
cov[z(w),z(x)]＝σ2r(θ,w,x)
[0142]
其中，θ＝[θ1,θ2,
…
,θn]
t
为相关性参数，r(θ,w,x)为表示变量θ,w,x相关性的函数且可以利用连续可微的高斯相关性函数来描述为：
[0143][0144]
其中，回归系数β及方差σ2可以用广义最小二乘回归方法表示为：
[0145]
β＝(f
t
r-1
f)-1ft
r-1y[0146][0147]
s32、在不确定性域中生成nc＝105个候选样本；
[0148]
s33、根据初始星滚柱丝杠副主动学习代理模型计算nc个样本点的估计值和期望风险的估计值取erf值最大的点为训练点x*，计算方法如下：
[0149][0150]
其中，sign(x)为符号函数，当x＞0时，sign(x)＝1，当x＜0时，sign(x)＝-1，φ()为标准正态分布的概率密度函数，ψ()为标准正态分布的累积分布函数；
[0151]
s34、设置阈值或收敛条件为ε＝10-5
；如果max(erf)》ε，增加x*作为新的训练点，更新行星滚柱丝杠副主动学习代理模型；
[0152]
s35、重复步骤s33～s35，直到max(erf)≤ε；
[0153]
s36、利用更新后的星滚柱丝杠副主动学习代理模型，采用拟蒙特卡洛方法产生抽样样本点，调用所建立的主动学习代理模型计算每组样本点对应的简化后的极限状态函数，对行星滚柱丝杠副进行不确定性分析，得到行星滚柱丝杠副在任一工况下的失效概率及可靠性灵敏度。
[0154]
所述采用拟蒙特卡洛方法产生抽样样本点，调用所建立的主动学习代理模型计算每组样本点对应的简化后的极限状态函数，对行星滚柱丝杠副进行不确定性分析，得到行
星滚柱丝杠副在任一工况下的失效概率及可靠性灵敏度，包括：
[0155]
步骤s361、对于行星滚柱丝杠副的每个随机变量xi在[0,1]的区间内生成 halton序列，各变量相互独立且均为正态分布，随机变量的累积概率分布函数 f(x
ij
)可表示为：
[0156][0157]
其中，x
ij
为第i个随机变量的第j个样本值，f(xi)为随机变量xi的概率密度函数，n为抽样样本数，为第x
ij
对应的halton数，其中halton序列的具体生成过程为：
[0158]
若q为任意质数，则任意自然数j有唯一的q进制表达式：
[0159]
j＝j0 j1q j2q2
···
jkqk[0160][0161]ji
∈{0,1,
···
,q-1}；i＝0,1,
···
,k
[0162]
其中，k表示lnj/lnq的整数部分，以q为底的基逆函数定义为：
[0163][0164]
对于任意自然数j＞0，均满足若前n个质数为q1,q2,
…
,qn，则 n维halton序列可以表示为：
[0165][0166]
步骤s362、获得随机变量x
ij
的样本值
[0167]
步骤s363、获得许用接触应力的样本点
[0168]
步骤s364、计算每组随机向量的样本xj＝(x
1j
,x
2j
,
…
,x
nj
)
t
作用下的载荷分布和局部接触特性，得到滚柱与丝杠或螺母接触侧上的最大接触应力，然后进一步计算极限状态函数g(xj)，如果g(xj)≤0，状态指示函数if(xj)＝1，否则if(xj)＝0；
[0169]
步骤s365、失效概率的估计及其变异系数计算如下：
[0170][0171][0172]
其中，nf为失效样本数；
[0173]
步骤s366、可靠性灵敏度的估计值如下：
[0174][0175]
其中，f
x
(x)为随机变量的联合概率密度函数，为基本随机变量xi的第k 个分布参数，mi为第i个随机变量xi的分布参数的数量，正态分布随机变量具有均值和标准差
两个分布参数，可靠性灵敏度可以计算为：
[0176][0177]
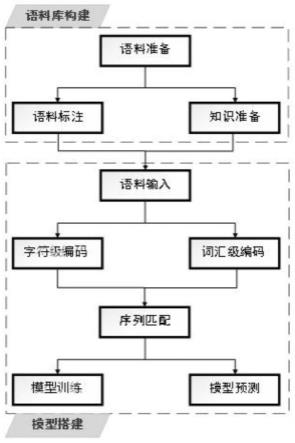
根据表1给出的行星滚柱丝杠副的随机结构参数，采用试验设计方法分析由图3所示流程中获得的2000组样本点，得到的不确定性因素对行星滚柱丝杠副承载特性与接触性能的重要度排序如图4所示。其中螺距对所有螺纹副中最大接触应力和最大载荷分布系数影响最大，滚柱螺纹牙型半角和中径对单对螺纹副接触应力影响最大。取前五个重要参数ps,pr,pn,βr和dr用于构建步骤s3 中的主动学习kriging代理模型。
[0178]
表1行星滚柱丝杠副的随机结构参数
[0179]
[0180][0181]
采用图3所示的计算流程，得到的行星滚柱丝杠副失效概率估计值与蒙特卡洛方法的收敛速度和计算耗时对比如图5所示。结果说明采用拟蒙特卡洛方法计算结果鲁棒性好，收敛速度快，计算效率高。对比采用5
×
106次抽样的蒙特卡洛方法、105次抽样的拟蒙特卡洛方法和本发明方法进行的行星滚柱丝杠副不确定性分析结果如表3所示。其中表3只列出了pr和ps的可靠性灵敏度，因为其余参数的可靠性灵敏很小。
[0182]
表3不确定性分析计算结果对比
[0183][0184]
[0185]
显然，拟蒙特卡洛方法和蒙特卡洛方法得到的失效概率和可靠性灵敏度的相对误差均小于1％。因此，在模拟次数较少的情况下，可以保证拟蒙特卡洛方法的精度，并有效减少计算时间。而alk-qmc方法可以显著减少极限状态函数调用的次数，进一步节省计算成本。此外，alk-qmc方法在增加6个训练调用的情况下，与蒙特卡洛方法得到的失效概率相比，相对误差为3.53％。由于alk-qmc方法对极限状态函数简化后只有五个随机变量，得到的可靠性灵敏度相对误差较大，但其结果仍可用于有效探究影响可靠性的主要因素。
[0186]
图6为由1600个halton样本点得到的行星滚柱丝杠副极限状态函数的三维网格曲面图，显示了最主要影响参数螺距与可靠性之间的关系。
[0187]
参照图6，在(a)图中，灰色曲面表示极限状态函数g(x)＝0，为安全域与失效域的分界面。灰色平面与网格曲面的交线用红色表示，黑点与红点分别为安全样本点与失效样本点。在(b)图中，而滚柱与螺母接触侧没有失效点。此外，在pr》ps和pr》pn的网格表面都存在使g(x)取得最大值的脊状结构区域，说明通过优化可以获得更高的可靠性，而远离脊状区域会增加失效概率。
[0188]
不同工况下的螺距与极限状态函数的三维网格曲面图如图7所示。当外载荷f不变时，接触疲劳极限σ
hlim
越大，失效样本点就越少；当σ
hlim
不变时，减小f也能降低失效概率，如20kn工况下没有失效点。因此，选择接触疲劳极限更高的材料，或者对行星滚柱丝杠副进行结构设计优化，在工况不变时使g(x) 取值最大，都可以提高行星滚柱丝杠副的可靠性。
[0189]
本发明优选实施例还公开了一种计算机可读存储介质，所述存储介质包括存储的程序，其中，所述程序执行上述实施例所述的行星滚柱丝杠副的不确定性分析方法。
[0190]
本发明优选实施例还公开了一种电子设备，包括：一个或多个处理器，存储器以及一个或多个程序，其中，所述一个或多个程序被存储在所述存储器中，并且被配置为由所述一个或多个处理器执行，所述一个或多个程序包括用于执行上述实施例所述的行星滚柱丝杠副的不确定性分析方法。
[0191]
本发明优选实施例还公开了一种行星滚柱丝杠副的不确定性分析系统，其包括以下模块：
[0192]
极限状态函数构建模块，用于通过结构参数、材料性能及边界条件求解行星滚柱丝杠副螺纹牙载荷分布和接触特性，考虑结构参数、材料性能及边界条件中存在的不确定性，基于s-n曲线和应力-强度干涉理论构建行星滚柱丝杠副螺纹牙接触疲劳失效模式下的极限状态函数；
[0193]
极限状态函数简化模块，用于引入确定性的低偏差点集halton序列，采用试验设计方法分析不确定性因素对行星滚柱丝杠副螺纹牙承载能力及接触性能影响的敏感性和贡献程度，将重要度排序靠前的参数作为随机变量来降低极限状态功能函数的维数，得到简化后的极限状态函数；
[0194]
不确定性分析模块，用于引入期望风险学习函数构建行星滚柱丝杠副主动学习代理模型，采用拟蒙特卡洛方法产生抽样样本点，调用所建立的主动学习代理模型计算每组样本点对应的简化后的极限状态函数，对行星滚柱丝杠副进行不确定性分析，得到行星滚柱丝杠副在任一工况下的失效概率及可靠性灵敏度。
[0195]
本发明实施例中的行星滚柱丝杠副的不确定性分析系统用于实现前述的行星滚柱丝杠副的不确定性分析方法，因此该系统的具体实施方式可见前文中的行星滚柱丝杠副
的不确定性分析方法的实施例部分，所以，其具体实施方式可以参照相应的各个部分实施例的描述，在此不再展开介绍。
[0196]
另外，由于本实施例的行星滚柱丝杠副的不确定性分析系统用于实现前述的行星滚柱丝杠副的不确定性分析方法，因此其作用与上述方法的作用相对应，这里不再赘述。
[0197]
以上实施例仅是为充分说明本发明而所举的较佳的实施例，本发明的保护范围不限于此。本技术领域的技术人员在本发明基础上所作的等同替代或变换，均在本发明的保护范围之内。本发明的保护范围以权利要求书为准。