自适应阻尼系数的广义极小残差大深度位场向下延拓方法

1.本发明涉及地球物理重磁领域的位场向下延拓技术领域，特别涉及一种自适应阻尼系数的广义极小残差大深度位场向下延拓方法。


背景技术：

2.位场向下延拓技术可以将重磁数据大深度向下延拓场源附近，突出了有用信息，被广泛应用在地质勘探中，而且位场向下延拓在水下磁性障碍物探测领域也发挥着重要的作用。此外，通过位场向下延拓技术构建重磁三维空间数据库还可以为辅助导航提供基础数据，以及位场的向下延拓运算也是许多重磁数据处理的核心步骤。然而在数学上，位场的向下延拓是典型的线性反问题，具有不稳定性，不能直接求解。一些研究就是基于改造频率域转换因子等手段来获得其向下延拓的稳定性，但获得的结果还是难以达到高精度勘探阶段科技工作者更高的期望。故而，稳定且高精度的位场向下延拓算法研究已经成为国际学术研究的前沿难点问题。
3.目前，较为广泛使用的位场向下延拓方法有积分迭代法与tikhonov正则化方法，其中积分迭代法具有延拓深度大，可达到10倍甚至20倍点距以上，效果好的特点，但是该方法的不足之处是在迭代过程中放大了噪声。而tikhonov正则化方法及改进的tikhonov正则化方法均存在正则化参数选取的问题，它对解的性态起着关键的作用，从而并没有从根本上解决计算的精度问题。
4.综上所述，针对位场向下延拓的不适定问题尽管相继出现了不同以及其改进的解决方案，但有的抗噪性能明显不足，其稳定性较差；有的对于正则化参数有很大的依赖性，其精度不足或稳定性较差。精度与稳定性是一对矛盾体，那么提出一种高精度与稳定性协调一致的位场向下延拓方法具有重要的现实意义。


技术实现要素：

5.针对上述问题，本发明旨在提供一种自适应阻尼系数的广义极小残差大深度位场向下延拓方法。
6.本发明的技术方案如下：
7.一种自适应阻尼系数的广义极小残差大深度位场向下延拓方法，包括以下步骤：
8.s1：获取实测二维平面位场数据，并将其网格化为规则点距的位场数据；
9.s2：将所述规则点距的位场数据按行重排为向量；
10.s3：确定位场向下延拓的深度，根据不同平面位场数据的关系，计算位场向下延拓的系数；
11.s4：根据等价关系将所述位场向下延拓的系数记为简记系数，并用所述简记系数表示位场向下延拓系数矩阵a；
12.s5：利用arnoldi算法生成正交基，获得krylov子空间的正交矩阵qk以及上hessenberg矩阵；
13.s6：建立最小二乘问题，并用lu分解法进行求解，获得基础解系系数dk；
14.s7：根据所述krylov子空间的正交矩阵qk以及所述基础解系系数dk，计算待延拓的位场列向量数据，并将所述位场列向量数据转换为待延拓的矩阵数据，获得向下延拓结果。
15.作为优选，步骤s3中，所述位场向下延拓的系数通过下式进行计算：
[0016][0017][0018]
式中：g(m,n,i,j)为位场向下延拓的系数；h为位场向下延拓的深度；δx、δy分别为x、y方向的网格化间距；r为计算点与异常体的位置关系函数；m、n分别为计算点的横、纵向网格点坐标；i、j分别为异常体的横、纵向网格点坐标。
[0019]
作为优选，步骤s4中，所述等价关系为：
[0020]
g(m,n,i,j)＝g(1,1,|m-i| 1,|n-j| 1)
ꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0021]
则g(m,n,i,j)的所述简记系数为g
|m-i| 1,|n-j| 1
；所述位场向下延拓系数矩阵a为：
[0022][0023]
表中，m、n分别为x、y方向的网格化总数。
[0024]
作为优选，步骤s5具体包括以下子步骤：
[0025]
给定初值x0＝us0，计算r0＝b-ax0，β＝
║
r0║
，q1＝r0/β，对i＝1,2,3
……
,k通过下式进行迭代：
[0026]hji
＝《aqi,qj》，j＝1,2,3
……iꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0027][0028][0029]
式中：x0为初始向量；us0为观测数据u0按行重排后的向量；r0为初始残差；b为高平面位场数据或观测数据；a为位场向下延拓系数矩阵；β为残差二范数；q1为归一化范数；h
ji
为向量内积；qi、qj分别为不同迭代次数下的归一化范数；为计算过程量；
[0030]
迭代完成后生成所述krylov子空间的正交矩阵qk以及所述上hessenberg矩阵；所述krylov子空间的正交矩阵qk为：
[0031]
qk＝[q1,q2,
…
qk]
ꢀꢀꢀꢀꢀꢀꢀ
(7)
[0032]
所述上hessenberg矩阵为：
[0033][0034]
式中：h
k(e)
为上hessenberg矩阵。
[0035]
作为优选，步骤s6中，所述最小二乘问题为：
[0036][0037][0038]
式中：dk为基础解系系数；e1为末尾为1，其余元素为0列向量；上标t代表转置。
[0039]
作为优选，步骤s6中，用lu分解法求解所述最小二乘问题具体包括以下子步骤：
[0040]
建立所述最小二乘问题的等价方程：
[0041][0042]
计算所述等价方程的系数矩阵可逆条件数λ：
[0043][0044]
当λ＜0.01时，通过求解如下方程获得所述基础解系系数dk：
[0045][0046]
式中：α2为阻尼系数；i为单位矩阵；
[0047]
当λ≥0.01时，通过求解公式(11)获得所述基础解系系数dk。
[0048]
作为优选，步骤s7中，待延拓的位场列向量数据通过下式进行计算：
[0049]
uh＝q
kdk
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(14)
[0050]
式中：uh为待延拓的位场列向量数据；
[0051]
将所述位场列向量数据转换为待延拓的矩阵数据具体为：
[0052]
uh＝{uh(1,1),uh(2,1),
…
uh(m,1),uh(1,2),uh(2,2),
…
uh(m,2),
……
uh(m,n)}
t
ꢀꢀꢀ
(15)
[0053]
公式(15)的结果即为所述向下延拓结果。
[0054]
本发明的有益效果是：
[0055]
本发明与普遍使用的积分迭代法及其改进方法相比，具有良好的抑制噪声能力；与普遍使用的tikhonov方法及其迭代法相比，不存在正则化参数的选取问题；本发明通过求解残差极小的k维最小二乘问题(k为迭代次数)，能够达到准确解的阶数最优，从而使得本发明具备高精度的特点，对位场勘探解释的精度改善具有实际意义。
附图说明
[0056]
为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本
发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其他的附图。
[0057]
图1为一个具体实施例磁异常等值线示意图；
[0058]
图2为图1所示实施例向下延拓20倍点距的结果示意图；
[0059]
图3为图1所示实施例在不同高噪声情况下向下延拓20倍点距的结果示意图；
[0060]
图4为一个具体实施例本发明与积分迭代法的计算结果对比示意图；
[0061]
图5为一个具体实施例本发明与不同正则化参数情况下的tikhonov迭代法的计算结果对比示意图。
具体实施方式
[0062]
下面结合附图和实施例对本发明进一步说明。需要说明的是，在不冲突的情况下，本技术中的实施例及实施例中的技术特征可以相互结合。需要指出的是，除非另有指明，本技术使用的所有技术和科学术语具有与本技术所属技术领域的普通技术人员通常理解的相同含义。本发明公开使用的“包括”或者“包含”等类似的词语意指出现该词前面的元件或者物件涵盖出现在该词后面列举的元件或者物件及其等同，而不排除其他元件或者物件。
[0063]
本发明提供一种自适应阻尼系数的广义极小残差大深度位场向下延拓方法，包括以下步骤：
[0064]
s1：获取实测二维平面位场数据，并将其网格化为规则点距的位场数据u0(mδx,nδy)。
[0065]
在一个具体的实施例中，为了表示方便将所述u0(mδx,nδy)记为u0(m,n)，其中m、n分别为计算点的横、纵向网格点坐标；δx、δy分别为x、y方向的网格化间距。
[0066]
s2：将所述规则点距的位场数据按行重排为向量，即：
[0067]
u0＝{u0(1,1),u0(2,1),
…
u0(m,1),u0(1,2),u0(2,2),
…
u0(m,2),
……
u0(m,n)}
t
ꢀꢀꢀ
(16)
[0068]
式中：u0为按行重排后的向量；m、n分别为x、y方向的网格化总数；上标t代表转置。
[0069]
s3：确定位场向下延拓的深度，根据不同平面位场数据的关系，计算位场向下延拓的系数。
[0070]
在一个具体的实施例中，所述位场向下延拓的系数通过下式进行计算：
[0071][0072][0073]
式中：g(m,n,i,j)为位场向下延拓的系数；h为位场向下延拓的深度；δx、δy分别为x、y方向的网格化间距；r为计算点与异常体的位置关系函数；i、j分别为异常体的横、纵向网格点坐标。
[0074]
s4：根据等价关系将所述位场向下延拓的系数记为简记系数，并用所述简记系数表示位场向下延拓系数矩阵a。
[0075]
在一个具体的实施例中，所述等价关系为：
[0076]
g(m,n,i,j)＝g(1,1,|m-i| 1,|n-j| 1)
ꢀꢀꢀꢀꢀꢀꢀ
(3)
[0077]
则g(m,n,i,j)的所述简记系数为g
|m-i| 1,|n-j| 1
；所述位场向下延拓系数矩阵a为：
[0078][0079]
s5：利用arnoldi算法生成正交基，获得krylov子空间的正交矩阵qk以及上hessenberg矩阵；具体包括以下子步骤：
[0080]
给定初值x0＝us0，计算r0＝b-ax0，β＝
║
r0║
，q1＝r0/β，对i＝1,2,3
……
,k通过下式进行迭代：
[0081]hji
＝《aqi,qj》，j＝1,2,3
……iꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0082][0083][0084]
式中：x0为初始向量；us0为观测数据u0按行重排后的向量；r0为初始残差；b为高平面位场数据或观测数据；a为位场向下延拓系数矩阵；β为残差二范数；q1为归一化范数；h
ji
为向量内积；qi、qj分别为不同迭代次数下的归一化范数；为计算过程量；
[0085]
迭代完成后生成所述krylov子空间的正交矩阵qk以及所述上hessenberg矩阵；所述krylov子空间的正交矩阵qk为：
[0086]
qk＝[q1,q2,
…
qk]
ꢀꢀꢀꢀꢀꢀ
(7)
[0087]
所述上hessenberg矩阵为：
[0088][0089]
式中：h
k(e)
为上hessenberg矩阵。
[0090]
s6：建立最小二乘问题，并用lu分解法进行求解，获得基础解系系数dk。
[0091]
在一个具体的实施例中，所述最小二乘问题为：
[0092][0093][0094]
式中：dk为基础解系系数；e1为末尾为1，其余元素为0列向量，其个数根据计算方程
的大小确定；上标t代表转置。
[0095]
用lu分解法求解所述最小二乘问题具体包括以下子步骤：
[0096]
建立所述最小二乘问题的等价方程：
[0097][0098]
计算所述等价方程的系数矩阵可逆条件数λ：
[0099][0100]
当λ＜0.01时，通过求解如下方程获得所述基础解系系数dk：
[0101][0102]
式中：α2为阻尼系数；i为单位矩阵；
[0103]
当λ≥0.01时，通过求解公式(11)获得所述基础解系系数dk。
[0104]
s7：根据所述krylov子空间的正交矩阵qk以及所述dk，计算待延拓的位场列向量数据，并将所述位场列向量数据转换为待延拓的矩阵数据，获得向下延拓结果。
[0105]
在一个具体的实施例中，待延拓的位场列向量数据通过下式进行计算：
[0106]
uh＝q
kdk
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(14)
[0107]
式中：uh为待延拓的位场列向量数据；
[0108]
将所述位场列向量数据转换为待延拓的矩阵数据具体为：
[0109]
uh＝{uh(1,1),uh(2,1),
…
uh(m,1),uh(1,2),uh(2,2),
…
uh(m,2),
……
uh(m,n)}
t
ꢀꢀꢀꢀ
(15)
[0110]
公式(15)的结果即为所述向下延拓结果。
[0111]
在一个具体的实施例中，通过以下模型试验检验本发明的有效性。采用球体在不同观察面的理论磁异常与向下延拓异常来检验本发明的计算效果，并分析均方误差(mean squared error，mse)与迭代次数的关系，及拟合数据的平均残差范数(meanresidual norm，mrn)与迭代次数的关系，来定量评价计算结果的精度、收敛性等。考虑到实际应用中，观测数据不可避免的含有一定的误差，因此将含噪声的理论数据也进行向下延拓计算，对其效果进行对比，并分析均方误差、平均残差范数与迭代次数的关系，进一步的探讨方法的适用性。
[0112]
所述均方误差通过下式进行计算：
[0113][0114]
式中：x和x
*
分别为向下延拓结果和理论值；l为用于计算的点数。
[0115]
所述拟合数据的平均残差范数定义为：
[0116][0117]
建立的球体模型参数如表1所示：
[0118]
表1球体模型的参数
[0119]
模型编号rx0(km)y0(km)r0(km)h0(km)m'(a/m)i0(
°
)a0(
°
)i'(
°
)a'(
°
)
110100.52.515060306026.56.50.52.51.250603060313.56.50.52.5150603060413.513.50.52.5150603060
[0120]
表1中(x0,y0,h0)为球体中心坐标，r0为球体半径，m'为磁化强度，i0、a0、i'和a'分别为地磁场倾角、剖面磁偏角、磁化强度倾角和剖面与磁北夹角，根据球体磁场的计算公式(坐标系z轴方向向下)，分别计算z＝1km平面与z＝0km平面的理论磁异常，结果如图1所示，其中图1(a)为z＝0km平面的理论磁异常等值线图，图1(b)为z＝0km平面含有1％噪声的理论磁异常等值线图，图1(c)为z＝1km平面的理论磁异常等值线图。在本实施例中，计算网格数为401
×
401，数据资料点距为50米。
[0121]
采用本发明所述自适应阻尼系数的广义极小残差大深度位场向下延拓方法，将图1(a)和图1(b)所示的磁异常数据向下延拓20倍点距至平面，计算结果如图2所示，其中图2(a)为均方误差与迭代次数的关系示意图，图2(b)为平均残差范数与迭代次数的关系示意图，图2(c)为无噪声情况下的计算结果，图2(d)为含噪声情况下的计算结果。
[0122]
从图2(a)与2(b)可以看出，在无噪声和含噪声情况下，均方误差和拟合数据的平均残差范数随着迭代次数的增加，其变化类似，为单调递减直至达到最后的收敛；另外，在无噪声和含噪声情况下，两者的均方误差相近，拟合数据的平均残差范数的差距也很小，具有良好的抗噪能力。
[0123]
从图2(c)与2(d)可以看出，在无噪声和含噪声情况下，对比两者的形态以及幅值大小，都基本保持一致，也说明了本发明抑制噪声能力较好，即稳定性好。
[0124]
为了进一步检验本发明方法的稳健性，对图1(a)所示的理论磁异常分别叠加噪声水平δ＝10％、20％以及30％的随机噪声，然后向下延拓20倍点距，计算结果如图3所示，其中图3(a)为不同噪声情况下计算结果的迭代次数与均方误差的关系示意图，图3(b)为对角线剖面的计算结果对比图，图3(c)为含10％噪声的计算结果，图3(d)为含20％噪声的计算结果，图3(e)为含30％噪声的计算结果。
[0125]
从图3(a)可以看出，在高噪声30％的情况下，收敛后的均方误差仍在1nt之下，本发明方法仍具有良好的稳健性。从图3(b)可以看出，在高噪声情况下，本发明除去边部有偏差，其余部分仍保持较高的精度。从图3(c)-图3(e)可以看出，其形态仍保持高度的一致性，且保幅性较好。
[0126]
为了进一步检验本发明方法的计算效果，采用目前较为广泛使用的积分迭代法和tikhonov迭代法对图1所示的同一模型数据进行试验，并分别与本发明的计算结果进行对比。
[0127]
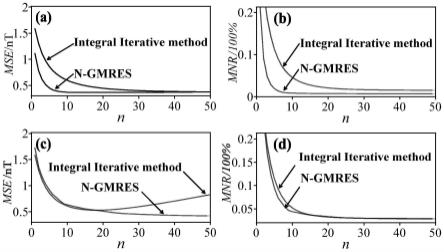
其中，采用本发明方法与积分迭代法分别向下延拓20倍点距时的对比结果如图4所示，其中图4(a)为无噪声情况下的均方误差与迭代次数的关系示意图，图4(b)为无噪声情况下的平均残差范数与迭代次数的关系示意图，图4(c)为含噪声情况下的均方误差与迭代次数的关系示意图，图4(d)为含噪声情况下的平均残差范数与迭代次数的关系示意图。从图4可以看出，在无噪声情况下，本发明方法相比积分迭代法收敛速度快，精度高。在含噪声情况下，积分迭代法随着迭代次数增加，计算结果的均方误差先减小后增大，表现出抗噪性能差。本发明方法不仅表现出了良好的收敛性，而且均方误差较小。
[0128]
采用本发明方法与不同正则化参数的tikhonov迭代法分别向下延拓20倍点距的对比结果如图5所示，其中图5(a)为无噪声情况下的均方误差与迭代次数的关系示意图，图5(b)为无噪声情况下的平均残差范数与迭代次数的关系示意图，图5(c)为含噪声情况下的均方误差与迭代次数的关系示意图，图5(d)为含噪声情况下的平均残差范数与迭代次数的关系示意图。从图5可以看出，在无噪声情况下，tikhonov迭代法依赖于正则化参数(alpha)的选择，不同的大小的正则化参数决定计算的精度，正则化参数过大，其计算结果的精度不高，正则化参数过小，也可能存在计算结果发散，而本发明方法稳定性好，同时表现出较高的计算精度。在含噪声情况下，tikhonov迭代法更加依赖于正则化参数的选择，而本发明方法仍表现出较强的稳定性和较高的计算精度。
[0129]
综上所述，相比普遍使用的积分迭代法及其改进方法，本发明所提方法具有良好的抑制噪声能力；相比普遍使用tikhonov方法及其迭代法，本发明所提方法不存在正则化参数的选取问题；且本发明通过求解残差极小的k维最小二乘问题，能够达到准确解的阶数最优，从而使得本发明方法具备高精度的特点，与现有技术相比，具有显著的进步。
[0130]
以上所述，仅是本发明的较佳实施例而已，并非对本发明作任何形式上的限制，虽然本发明已以较佳实施例揭露如上，然而并非用以限定本发明，任何熟悉本专业的技术人员，在不脱离本发明技术方案范围内，当可利用上述揭示的技术内容作出些许更动或修饰为等同变化的等效实施例，但凡是未脱离本发明技术方案的内容，依据本发明的技术实质对以上实施例所作的任何简单修改、等同变化与修饰，均仍属于本发明技术方案的范围内。