一种含表面脱碳层的梁类锻件弯曲变形计算方法

1.本发明涉及梁类锻件的弯曲变形、承载能力分析设计领域，尤其涉及一种含表面脱碳层的梁类锻件弯曲变形计算方法。


背景技术：

2.前轴是汽车上的重要承力构件，除了承受汽车的重量外，还承受地面和车架之间的垂直载荷、制动力、侧向力以及侧向力所引起的弯矩等，要求其具有很高的强度、韧性综合力学性能。目前前轴一般采用热锻成形工艺制造，需将40cr、42crmo、50号钢等坯料加热至900～1200℃，经过预锻、终锻成形，并进行淬火回火热处理。由于钢制坯料在高温存在时间较长，环境中的h2o、co2、o2、h2将零件表面的fe3c还原生成co及ch4等，当还原反应强于氧化反应时，材料表面碳含量显著降低，即锻件表面发生了脱碳，且随着时间的增长碳原子持续向外扩散，脱碳层深度不断增加。锻件表面的脱碳导致后续调质热处理后表面马氏体含量降低，甚至形成完全脱碳的铁素体表层，强度硬度显著降低，且密度、弹性模量、组织力学性能分布与内部不连续，在承受弯曲载荷时横截面的应变、应力分布情况改变，严重影响着汽车前轴锻件的疲劳强度和承载能力。目前前轴梁类锻件的设计计算将其视为匀质材料，并采用简化的平截面假设方法，忽略截面剪应力，根据截面静矩、惯性矩、给定载荷计算最大应力和弯曲变形。而表面脱碳导致横截面材料弹性模量、泊松比、密度等物性参数呈非线性分布变化，截面应变应力分布情况更为复杂，采用传统简化方法无法计算脱碳非均匀材料条件下应力、应变分布情况，给前轴梁类锻件的分析设计带来困难。


技术实现要素：

3.本发明的目的是克服现有技术中存在的计算准确度低的缺陷与问题，提供一种计算准确度高的含表面脱碳层的梁类锻件弯曲变形计算方法。
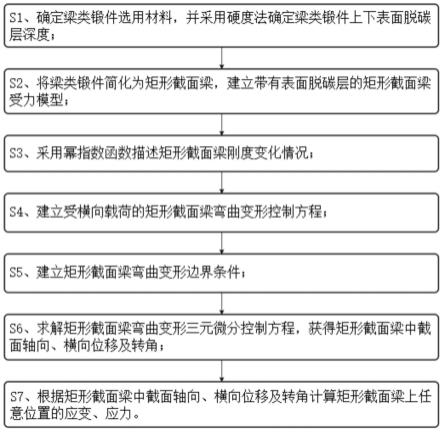
4.为实现以上目的，本发明的技术解决方案是：一种含表面脱碳层的梁类锻件弯曲变形计算方法，该方法包括以下步骤：
5.s1、确定梁类锻件选用材料，并采用硬度法确定梁类锻件上下表面脱碳层深度；
6.s2、将梁类锻件简化为矩形截面梁，建立带有表面脱碳层的矩形截面梁受力模型；
7.s3、采用幂指数函数描述矩形截面梁刚度变化情况；
8.s4、建立受横向载荷的矩形截面梁弯曲变形控制方程；
9.s5、建立矩形截面梁弯曲变形边界条件；
10.s6、求解矩形截面梁弯曲变形三元微分控制方程，获得矩形截面梁中截面轴向、横向位移及转角；
11.s7、根据矩形截面梁中截面轴向、横向位移及转角计算矩形截面梁上任意位置的应变、应力。
12.步骤s2中，矩形截面梁的左端点为固定铰支座，右端点为移动铰支座；坐标系x轴零点位于矩形截面梁的左端点，y轴零点位于矩形截面梁的中截面位置；
13.根据矩形截面梁的总长度、宽度、高度、横向集中载荷、脱碳层深度，建立带有表面脱碳层的矩形截面梁受力模型。
14.步骤s3中，矩形截面梁截面上不同位置的有效弹性模量e(z)为：
15.e(z)＝e
fvf
e
mvm
[0016][0017]vf
vm＝1
[0018]
式中，ef为纯铁素体弹性模量；vf为纯铁素体体积分数；em为纯马氏体弹性模量；vm为纯马氏体体积分数；h1为矩形截面梁下表面脱碳层深度位置z方向坐标值，h为矩形截面梁的高度，d1为矩形截面梁下表面脱碳层深度；h2为矩形截面梁上表面脱碳层深度位置z方向坐标值，d2为矩形截面梁上表面脱碳层深度；p为脱碳层材料梯度指数，p∈(0， ∞)。
[0019]
步骤s4具体包括以下步骤：
[0020]
s41、根据三阶剪切变形理论建立矩形截面梁上各点位移场：
[0021][0022]
式中，u(x，z)、v(x，z)、w(x，z)分别为矩形截面梁上任意一点x、y、z方向的轴向位移和横向位移；u0(x)、w0(x)分别为矩形截面梁中截面上的轴向位移和横向位移；φ(x)为矩形截面梁横截面上中轴位置的点绕y轴的转角；
[0023]
s42、根据变形体虚功原理建立矩形截面梁弯曲变形控制方程：
[0024][0025]
式中，α＝4/3h2，β＝4/h2，q为矩形截面梁上各处所受横向分布载荷；a1、a2、a3、b1、b2、b3、c1、c2、c3、d1、d2、f1、f2都为系数，具体计算公式为：
[0026][0027]
式中，g(z)为剪切模量，g(z)＝e(z)/[2(1 v)]，v为材料泊松比。
[0028]
步骤s5中，矩形截面梁左端点的边界条件为：
[0029][0030]
矩形截面梁右端点的边界条件为：
[0031][0032]
步骤s6中，将u0(x)、φ(x)、w0(x)进行傅里叶级数变换得到如下变换式：
[0033][0034]
式中，un为轴向位移傅里叶级数各项系数；φn为转角傅里叶级数各项系数；wn为横向位移傅里叶级数各项系数；l为矩形截面梁的总长度；
[0035]
通过狄克拉函数将离散集中载荷进行连续化，如下式所示：
[0036]
q(x)＝f
cl
δ(x-x
l
) f
c2
δ(x-x2)
[0037][0038][0039]
式中，δ(x)为狄克拉函数；x1为集中载荷f
c1
作用位置距离矩形截面梁左端点的距离；x2为集中载荷f
c2
作用位置距离矩形截面梁左端点的距离；qn为载荷傅里叶级数的各项系数；
[0040]
将变换式及u0(x)、φ(x)、w0(x)的各阶导数代入矩形截面梁弯曲变形控制方程，并将求解得到的{u1，u2，u3，...，un}、{φ1，φ2，φ3，...，φn}、{w1，w2，w3，...，wn}代入变换式中，得到矩形截面梁上中轴线任意xi坐标位置的轴向位移u0(xi)、转角φ(xi)、横向位移w0(xi)。
[0041]
步骤s7中，矩形截面梁上各点位移场公式对x求导得到：
[0042][0043]
式中，ε
x
为轴向应变；γ
xz
为剪切应变；
[0044]
将矩形截面梁上中轴线任意xi坐标位置的轴向位移u0(xi)、转角φ(xi)、横向位移w0(xi)代入上式得到矩形截面梁上任意位置的应变；
[0045]
矩形截面梁上任意位置的轴向应力σ
x
、剪应力τ
xz
为：
[0046][0047]
与现有技术相比，本发明的有益效果为：
[0048]
本发明一种含表面脱碳层的梁类锻件弯曲变形计算方法可以弥补传统梁类锻件
设计方法的不足，能准确计算带有不同深度表面脱碳层的前轴梁类锻件的弯曲变形、应力应变响应，分析梁类锻件组织非均匀性对承载能力的影响。
附图说明
[0049]
图1是本发明一种含表面脱碳层的梁类锻件弯曲变形计算方法的流程图。
[0050]
图2是本发明的实施例中的带有表面脱碳层的矩形截面梁受力模型示意图。
[0051]
图3是本发明的实施例中的不同脱碳层材料梯度指数p下的矩形截面梁弯曲横向位移示意图。
[0052]
图4是本发明的实施例中的不同脱碳层材料梯度指数p下的矩形截面梁弯曲转角示意图。
[0053]
图5是本发明的实施例中的带有表面脱碳层的矩形截面梁上x＝425mm位置轴向应力分布示意图。
[0054]
图6是本发明的实施例中的带有表面脱碳层的矩形截面梁上x＝425mm位置剪应力分布示意图。
具体实施方式
[0055]
以下结合附图说明和具体实施方式对本发明作进一步详细的说明。
[0056]
参见图1，一种含表面脱碳层的梁类锻件弯曲变形计算方法，该方法包括以下步骤：
[0057]
s1、确定梁类锻件选用材料，并采用硬度法确定梁类锻件上下表面脱碳层深度；
[0058]
s2、将梁类锻件简化为矩形截面梁，建立带有表面脱碳层的矩形截面梁受力模型；
[0059]
s3、采用幂指数函数描述矩形截面梁刚度变化情况；
[0060]
s4、建立受横向载荷的矩形截面梁弯曲变形控制方程；
[0061]
s5、建立矩形截面梁弯曲变形边界条件；
[0062]
s6、求解矩形截面梁弯曲变形三元微分控制方程，获得矩形截面梁中截面轴向、横向位移及转角；
[0063]
s7、根据矩形截面梁中截面轴向、横向位移及转角计算矩形截面梁上任意位置的应变、应力。
[0064]
步骤s2中，矩形截面梁的左端点为固定铰支座，右端点为移动铰支座；坐标系x轴零点位于矩形截面梁的左端点，y轴零点位于矩形截面梁的中截面位置；
[0065]
根据矩形截面梁的总长度、宽度、高度、横向集中载荷、脱碳层深度，建立带有表面脱碳层的矩形截面梁受力模型。
[0066]
步骤s3中，矩形截面梁截面上不同位置的有效弹性模量e(z)为：
[0067]
e(z)＝e
fvf
e
mvm
[0068][0069]vf
vm＝1
[0070]
式中，ef为纯铁素体弹性模量；vf为纯铁素体体积分数；em为纯马氏体弹性模量；vm为纯马氏体体积分数；h1为矩形截面梁下表面脱碳层深度位置z方向坐标值，h为矩形截面梁的高度，d1为矩形截面梁下表面脱碳层深度；h2为矩形截面梁上表面脱碳层深度位置z方向坐标值，d2为矩形截面梁上表面脱碳层深度；p为脱碳层材料梯度指数，p∈(0， ∞)。
[0071]
步骤s4具体包括以下步骤：
[0072]
s41、根据三阶剪切变形理论建立矩形截面梁上各点位移场：
[0073][0074]
式中，u(x，z)、v(x，z)、w(x，z)分别为矩形截面梁上任意一点x、y、z方向的轴向位移和横向位移；u0(x)、w0(x)分别为矩形截面梁中截面上的轴向位移和横向位移；φ(x)为矩形截面梁横截面上中轴位置的点绕y轴的转角；
[0075]
s42、根据变形体虚功原理建立矩形截面梁弯曲变形控制方程：
[0076][0077]
式中，α＝4/3h2，β＝4/h2，q为矩形截面梁上各处所受横向分布载荷；a1、a2、a3、b1、b2、b3、c1、c2、c3、d1、d2、f1、f2都为系数，具体计算公式为：
[0078][0079]
式中，g(z)为剪切模量，g(z)＝e(z)/[2(1 v)]，v为材料泊松比。
[0080]
步骤s5中，矩形截面梁左端点的边界条件为：
[0081][0082]
矩形截面梁右端点的边界条件为：
[0083][0084]
步骤s6中，将u0(x)、φ(x)、w0(x)进行傅里叶级数变换得到如下变换式：
[0085][0086]
式中，un为轴向位移傅里叶级数各项系数；φn为转角傅里叶级数各项系数；wn为横向位移傅里叶级数各项系数；l为矩形截面梁的总长度；
[0087]
通过狄克拉函数将离散集中载荷进行连续化，如下式所示：
[0088]
q(x)＝f
c1
δ(x-x1) f
c2
δ(x-x2)
[0089]
[0090][0091]
式中，δ(x)为狄克拉函数；x1为集中载荷f
c1
作用位置距离矩形截面梁左端点的距离；x2为集中载荷f
c2
作用位置距离矩形截面梁左端点的距离；qn为载荷傅里叶级数的各项系数；
[0092]
将变换式及u0(x)、φ(x)、w0(x)的各阶导数代入矩形截面梁弯曲变形控制方程，并将求解得到的{u1，u2，u3，...，un}、{φ1，φ2，φ3，...，φn}、{w1，w2，w3，...，wn}代入变换式中，得到矩形截面梁上中轴线任意xi坐标位置的轴向位移u0(xi)、转角φ(xi)、横向位移w0(xi)。
[0093]
步骤s7中，矩形截而梁上各点位移场公式对x求导得到：
[0094][0095]
式中，ε
x
为轴向应变；γ
xz
为剪切应变；
[0096]
将矩形截面梁上中轴线任意xi坐标位置的轴向位移u0(xi)、转角φ(xi)、横向位移w0(xi)代入上式得到矩形截面梁上任意位置的应变；
[0097]
矩形截面梁上任意位置的轴向应力σ
x
、剪应力τ
xz
为：
[0098][0099]
本发明的原理说明如下：
[0100]
本设计能够描述表面存在一定深度脱碳层的前轴梁类锻件的截面性能非线性变化，并计算其弯曲变形、应力应变，克服传统匀质材料梁平截面假设的不足，为表面脱碳非匀质前轴梁类锻件的设计提供依据。
[0101]
实施例：
[0102]
参见图1，一种含表面脱碳层的梁类锻件弯曲变形计算方法，该方法包括以下步骤：
[0103]
s1、确定梁类锻件选用材料为42crmo，并截取梁类锻件横截面试样，采用硬度法确定梁类锻件上下表面脱碳层深度d1、d2；
[0104]
s2、将梁类锻件简化为矩形截面梁，建立带有表面脱碳层的矩形截面梁受力模型；
[0105]
矩形截面梁的左端点为固定铰支座，右端点为移动铰支座；坐标系x轴零点位于矩形截面梁的左端点，y轴零点位于矩形截面梁的中截面位置；
[0106]
根据矩形截面梁的总长度l＝1900mm、宽度b＝90mm、高度h＝108mm、横向集中载荷f
c1
＝f
c2
＝70000n、脱碳层深度d1和d2，建立带有表面脱碳层的矩形截面梁受力模型，如图2所示；
[0107]
s3、采用幂指数函数描述矩形截面梁刚度变化情况；由于脱碳层表面为完全脱碳
的铁素体，内部未脱碳区域为马氏体，即由表向里铁素体含量逐渐降低，马氏体含量逐渐升高；
[0108]
矩形截面梁截面上不同位置的有效弹性模量e(z)为：
[0109]
e(z)＝e
fvf
e
mvm
[0110][0111]vf
vm＝1
[0112]
式中，ef为纯铁素体弹性模量，为178gpa；vf为纯铁素体体积分数；em为纯马氏体弹性模量，为215gpa；vm为纯马氏体体积分数；h
l
为矩形截面梁下表面脱碳层深度位置z方向坐标值，h为矩形截面梁的高度，d1为矩形截面梁下表面脱碳层深度；h2为矩形截面梁上表面脱碳层深度位置z方向坐标值，d2为矩形截面梁上表面脱碳层深度；p为脱碳层材料梯度指数，p∈(0， ∞)；
[0113]
s4、建立受横向载荷的矩形截面梁弯曲变形控制方程；具体包括以下步骤：
[0114]
s41、根据三阶剪切变形理论建立矩形截面梁上各点位移场：
[0115][0116]
式中，u(x，z)、v(x，z)、w(x，z)分别为矩形截面梁上任意一点x、y、z方向的轴向位移和横向位移；u0(x)、w0(x)分别为矩形截面梁中截面(z＝0)上的轴向位移和横向位移；φ(x)为矩形截面梁横截面上中轴位置的点绕y轴的转角；
[0117]
s42、根据变形体虚功原理建立矩形截面梁弯曲变形控制方程：
[0118][0119]
式中，α＝4/3h2，β＝4/h2，q为矩形截面梁上各处所受横向分布载荷；a1、a2、a3、b1、b2、b3、c1、c2、c3、d1、d2、f1、f2都为系数，具体计算公式为：
[0120][0121]
式中，g(z)为剪切模量，g(z)＝e(z)/[2(1 v)]，v为材料泊松比；
[0122]
s5、建立梁左边端点固定铰支、右边端点移动铰支矩形截面梁弯曲变形边界条件，其受力条件与图2中的模型一致；
[0123]
矩形截面梁左端点(x＝0)的边界条件为：
[0124][0125]
矩形截面梁右端点(x＝l)的边界条件为：
[0126][0127]
s6、采用navier方法求解矩形截面梁弯曲变形三元微分控制方程，获得矩形截面
梁中截面轴向、横向位移及转角；
[0128]
将u0(x)、φ(x)、w0(x)进行傅里叶级数变换得到如下变换式，变换式满足上述边界条件：
[0129][0130]
式中，un为轴向位移傅里叶级数各项系数；φn为转角傅里叶级数各项系数；wn为横向位移傅里叶级数各项系数；l为矩形截面梁的总长度；
[0131]
通过狄克拉函数将离散集中载荷进行连续化，如下式所示：
[0132]
q(x)＝f
c1
δ(x-x1) f
c2
δ(x-x2)
[0133][0134][0135]
式中，δ(x)为狄克拉函数；x1为集中载荷f
c1
作用位置距离矩形截面梁左端点的距离，x1＝532mm；x2为集中载荷f
c2
作用位置距离矩形截面梁左端点的距离，x2＝1368mm；qn为载荷傅里叶级数的各项系数；
[0136]
将变换式及u0(x)、φ(x)、w0(x)的各阶导数代入矩形截面梁弯曲变形控制方程，并将求解得到的{u1，u2，u3，...，un}、{φ1，φ2，φ3，...，φn}、{w1，w2，w3，...，wn}代入变换式中，得到矩形截面梁上中轴线任意xi坐标位置的轴向位移u0(xi)、转角φ(xi)、横向位移w0(xi)；不同脱碳层材料梯度指数p下的矩形截面梁弯曲横向位移和转角如图3、图4所示；
[0137]
s7、根据矩形截面梁中截面轴向、横向位移及转角计算矩形截面梁上任意位置的应变、应力；
[0138]
矩形截面梁上各点位移场公式对x求导得到：
[0139][0140]
式中，ε
x
为轴向应变；γ
xz
为剪切应变；
[0141]
将矩形截面梁上中轴线任意xi坐标位置的轴向位移u0(xi)、转角φ(xi)、横向位移w0(xi)代入上式得到矩形截面梁上任意位置的应变；
[0142]
矩形截面梁上任意位置的轴向应力σ
x
、剪应力τ
xz
为：
[0143][0144]
矩形截面梁上x＝425mm位置轴向应力和剪应力分布如图5、图6所示。