芯片制造中晶圆注入离子环节的高精度电通量计算方法

1.本发明属于芯片制造技术领域，具体涉及一种针对芯片制造过程中晶圆注入离子环节的高精度电通量计算方法。


背景技术：

2.芯片是集成电路的载体，它是集成电路经过设计、制造、封装、测试后得到的具有高集成度的一种元器件。芯片在新能源、信息通讯、电子产品、军事等领域都具有广泛应用，现代人的生活也与芯片息息相关。若是没有芯片，我们身边的高科技产品，如手机、电脑、智能家居、机器人等就成了一堆没有灵魂的废铁，通讯系统将陷入瘫痪；若是没有芯片，我国高速发展的人工智能将成为空中楼阁。因此，一个国家制造芯片的技术，在某种程度上代表了该国的信息技术水平，也是综合科技实力的体现。但与发达国家相比，我国芯片的自主研发和制造能力仍存在很大的差距，尽管目前国有芯片已经问世，但制作更小尺寸的高性能芯片技术仍然任重而道远。
3.芯片制作的核心是半导体集成电路工艺，即硅片用作基层，然后使用光刻、掺杂、cmp等技术制成晶圆等组件，再利用薄膜和cmp技术制成导线，完成封装和测试后便得到了芯片。其中晶圆的制作过程犹为关键，要对硅晶圆进行光刻、离子注入、最后蚀刻，对制作晶圆来说，这些步骤很可能不止做一次，而是需要反复的做以达到要求；而离子注入是在硅晶圆不同的位置加入不同的杂质，如p型物质或n型物质，不同杂质根据浓度、位置的不同就组成了晶体管。
4.制作高质量芯片的关键是晶体管的成本和性能，目前大部分芯片技术使用的都是场效应晶体管，而金属氧化物半导体场效应晶体管(简称mosfet)因为具有制造成本低廉、使用面积较小、高整合度的优势在晶体管中备受青睐，在半导体工厂中，进一步缩小mosfet的尺寸成为当下一项重要而迫切的任务。mosfet尺寸缩小有三个好处：一是通过的电流更多；二是切换速度变快；三是制造芯片的成本降低，这就大大提升了集成电路的效能。在过去几十年中，mosfet的尺寸在不断变小，如今已成功达到微米级别，但是mosfet的尺寸在进入亚微米范围时会产生短通道效应，这对进一步缩小mosfet的尺寸造成了很大的困难。
5.短通道效应会改变阈值电压和电子的移动特性，这使得在离子注入时无法设计出合适的杂质浓度来准确控制门路的电流和电压。文献[tiao lu,gang du,xiaoyan liu,and pingwen zhang.a finite volume method for the multi subband boltzmann equation with realistic 2d scattering in double gate mosfets.communications in computational physics,10(2):305-338,2011]提出了一种纳米尺度的双栅mosfet模型，并给出了二维电子在该模型下多子带玻尔兹曼输运方程(msbte)的求解器，该求解器的目标是确定制作晶圆时，在离子注入环节所需要的杂质浓度，而msbte的输运部分可以分裂成两个输运方程，每个输运方程在经过某种坐标变换后可以转换为标量守恒律：
[0006]
[0007]
或平流方程：
[0008][0009]
其中：是密度函数，是给定向量场。
[0010]
使用有限体积方法(finite volume method，fvm)高精度数值求解的核心问题是计算在时间区间[t0,te]内穿过某固定曲面的欧拉通量积分：
[0011][0012]
其中：a与分别为上的面积元和单位法向量。
[0013]
此外该文献还提出了一种基于正通量守恒(positive and flux conservative，pfc)法的二阶有限体积法用来离散msbte的输运方程，其本质就是计算电通量，电通量积分在有限体积法中有重要作用。对于多相流界面追踪，vof(volume-of-fluid)方法在对流步中计算穿过控制体边界的通量阶段的精度取决于其中通量计算的精度；在用传统的fvm数值求解标量守恒律时，我们取控制体的边界为固定曲面然后通过的欧拉通量就被离散为函数f控制体平均值的线性组合，这种空间离散使得式(1)变成常微分方程组，最后再调用时间积分方法对这一系统进行数值求解，我们称这种离散方法为直线法(method-of-lines，mol)。
[0014]
前面提到的fvm与mol在过去几十年中一直备受欢迎，但仍然存在缺陷，例如当标量函数f可积但不连续时，这些方法难以达到较高的收敛速度。此外，即使f是光滑的，在fvm-mol求解过程中，时间步长也将受到cfl条件(courant-friedrichs-lewy)的限制，这极大地影响了算法的效率。因此，为了弥补fvm-mol方法在数值上的缺陷，我们通过通量恒等式将欧拉通量积分转换为拉格朗日通量积分：
[0015][0016]
其中：等式右侧的通量指标表示初始位置在中的粒子在时间[t0,te]内穿过曲面的净次数。
[0017]
我们将等式右侧称为拉格朗日通量积分，通过数值计算拉格朗日通量积分可以得到对欧拉通量积分的逼近，我们把这种方法叫做拉格朗日通量计算(lagrangian flux calculation，lfc)。相对于直接计算欧拉通量积分，lfc不需要在全局范围内求解标量守恒律方程，只需要在一个很小的局部范围内利用标量函数的初值计算积分即可。这种lfc方法实现简单，还能使算法实现高精度并且具有二、四、六阶收敛。通量恒等式不仅大大提高了芯片中计算电通量的效率，还能用于解决关于输运、混合等实际问题中的通量问题。
[0018]
在现有文献中，对于二维空间中穿过固定曲线的拉格朗日通量的研究已经十分深入，而其中捐献区间的概念对拉格朗日通量的发展起到了至关重要的作用。最早在基于双曲守恒律的有限体积算法中曾提到了捐献区间的雏形，在多相流的数值模拟中，捐献区间
的概念被用于两种流体之间的界面追踪，然而相关文献或方法只提供了捐献区间的隐式概念，并没有在数学上给出准确定义。
[0019]
文献[qinghai zhang.on donating regions:lagrangian flux through a fixed curve.siam review,55(3):443-461,2013]基于脉线和时间线提出了二维空间上穿过简单固定曲线的捐献区间的显式定义，并在一定几何与时间步长限制下，证明了捐献区间等价于穿过简单曲线净通量仅为一次的所有粒子的集合，从而得到如下在二维空间上成立的等式：
[0020][0021]
其中：f与u满足标量守恒律，并且捐献区间满足：(1)简单曲线的两个端点l,n的向后脉线既不相交也不自交；(2)简单曲线属于捐献区间的边界；(3)捐献区间有可数个自交点。
[0022]
文献[qinghai zhang.highly accurate lagrangian flux calculation via algebraic quadratures on spline-approximated donating regions.computer methods in applied mechanics and engineering,264:191-204,2013]基于式(5)提出了一种数值lfc算法，记为lfc-2013。lfc-2013从给定的速度场u构造捐献区间并用样条函数逼近，然后通过格林公式和一维数值求积公式计算捐献区间上的拉格朗日通量积分。lfc-2013在算法上具有四、六、八阶收敛精度，但在实现时往往需要将时间区间做足够细分，然后对每个时间段进行数值积分，再相加得到总的数值通量积分，这破坏了我们仅需要函数f的初始时刻值的条件，进而削弱了lfc计算通量积分的优势。
[0023]
文献[qinghai zhang.on generalized donating regions:classifying lagrangian fluxing particles through a fixed curve in the plane.journal of mathematical analysis and applications,424(2):861-877,2015]提出了一种穿过简单固定曲线的广义捐献区间与通量指标为n的捐献区间的定义，其中广义捐献区间由通量指标为n的捐献区间组成，并在两个端点l,n的向后脉线既不相交也不自交的条件下，证明了通量指标为n的捐献区间穿过简单曲线的净通量为n次，从而得到如下在二维空间上的等式：
[0024][0025]
文献[daniel karrasch.lagrangian transport through surfaces in volume-preserving flows.siam journal on applied mathematics,76(3):1178-1190,2016]给出了式(6)在二维及更高维空间的证明，并且文献[florian hofherr and daniel karrasch.lagrangian transport through surfaces in compressible flows.siam journal on applied dynamical systems,17(1):526-546,2018]还给出了基于式(6)的数值计算二维lfc的方法，记为lfc-hk；lfc-hk算法的主要思想是构建捐献区间的边界将
边界划分成互不相交的简单闭曲线的集合，计算每个子捐献区间的环绕数与积分，最后将权重相加得到总的数值通量积分，然而lfc-hk的算法只有二阶精度，在计算曲线段的交点时过程较为繁琐且容易出现病态情况。
[0026]
文献[qinghai zhang and lingyun ding.lagrangian flux calculation through afixed planar curve for scalar conservation laws.siam journal on scientific computing,41(6):a3596-a3623,2019]给出了式(6)在二维空间上的证明和穿过固定曲线的二维数值计算lfc的算法，记为lfc-2019；与lfc-hk算法不同的是，lfc-2019算法并不直接计算式(6)右端的积分，而是首先证明了如下等式：
[0027][0028]
其中：然后通过数值计算式(7)右端的积分，得到欧拉通量积分，数值算法中用了样条函数对捐献区间的边界进行逼近，然后使用一维高斯积分公式，他们通过数值测试验证了lfc-2019算法可以达到二、四、六阶收敛。
[0029]
综上分析可知，用fvm法求解标量守恒律中的标量函数f时，一般的做法是，将时间区间[tn,tn k]进行划分，然后由f在初始时刻的控制体平均值来计算这段时间区间内穿过控制体边界的通量，从而得到f在终止时刻的控制体平均值，在通过反复迭代且不断产生f的中间量之后，就得到了f(tn k)的近似值，这整个过程都非常的繁琐和冗杂；但通过通量恒等式，我们只需要给定f的初始值，无需在每个时间步中层层推进就可以得到f(tn k)的近似值，整个过程就变得简单且容易实现。欧拉通量积分在fvm法中具有重要作用，但直接计算欧拉通量会出现两个弊端：一是当标量函数f可积但不连续时，直接计算欧拉通量将难以达到较高的收敛速度；二是即使标量函数f是光滑的，在fvm-mol求解过程中，时间步长也将受到cfl条件的限制，这极大地影响了算法的效率。
[0030]
在lfc-2013中，时间步长需要受到一定的限制，才能使式(5)成立，所以在实现lfc-2013的算法时，需要将时间区间做足够的细分，然后对每个时间段进行数值积分，再相加得到总的数值通量积分，故lfc-2013破坏了我们仅需要函数f的初始时刻值的条件，进而削弱了lfc计算通量积分的优势。
[0031]
lfc-hk算法有三个缺点：一是在计算曲线段的交点时过程较为繁琐且容易产生病态情况；二是lfc-hk算法只有二阶精度；三是lfc-hk算法只适用于二维通量积分的计算，若推广至三维将具有很大的困难。
[0032]
lfc-2019算法只实现了二维穿过固定曲线的lfc算法，还没有实现穿过动曲线的lfc算法，而且也没有实现三维的lfc算法；另外，lfc-2019算法中在增大时间区间时，部分数值积分会出现降阶现象。


技术实现要素：

[0033]
鉴于上述，本发明提供了一种针对芯片制造过程中晶圆注入离子环节的高精度电通量计算方法，通过对lfc-2019算法中的二维数值积分算法进行有效改进，使得积分算法通过增加样条节点数就能实现收敛，运用二维lfc-2019的思想，实现了具有高精度的三维
lfc算法且达到了二、四、六阶收敛率。
[0034]
一种针对芯片制造过程中晶圆注入离子环节的高精度电通量计算方法，包括如下步骤：
[0035]
(1)首先确定三维空间中的流速场u(x,t)、初始时间粒子的浓度函数f(x,t0)以及固定曲面其中x为三维空间中任一点的位置信息，t表示时间，t0表示初始时刻；
[0036]
(2)根据流速场u(x,t)构造一个流映射φ；
[0037]
(3)根据流映射φ构造向后脉线其表示时间段t0～t0 k内通过位置m的所有粒子的集合；
[0038]
(4)利用流映射φ、向后脉线和固定曲面构造生成曲面
[0039]
(5)利用浓度函数f(x,t0)和生成曲面计算时间段t0～t0 k内粒子穿过固定曲面的电通量i。
[0040]
步骤(4)很关键，其物理意义是构造一个区域即生成曲面在这个区域内的所有粒子都将会穿过固定曲面本发明中向晶圆注入的离子即为一种粒子。
[0041]
进一步地，所述步骤(1)中的流速场u(x,t)与浓度函数f(x,t0)需满足标量守恒律。满足标量守恒律的物理意义是质量守恒，即这个空间内的粒子既不会凭空消失也不会凭空出现。
[0042]
进一步地，所述步骤(2)中的流映射φ对于三维空间中任一点p，其初始时刻的位置为x0，能够计算流速场u(x,t)作用下点p在t0 k时刻的位置x(t0 k)，k为实数。
[0043]
进一步地，所述步骤(4)的具体实现过程如下：
[0044]
4.1首先在固定曲面上均匀取点，得到点集s1，点集s1包含了曲面及其边界上的点；
[0045]
4.2根据点集s1中各点在t0 k时刻的位置利用流映射φ反推各点在初始时刻的位置，进而根据这些位置信息拟合出所有点在初始时刻共同所在的曲面
[0046]
4.3对于点集s1中的任一边界点q，计算该点的向后脉线进而根据边界点的向后脉线信息拟合出所有边界点在初始时刻共同所在的曲面
[0047]
4.4取固定曲面曲面以及曲面的并集，得到生成曲面
[0048]
进一步地，所述向后脉线表示在t0至t0 k这段时间内通过位置q的所有粒子的集合，q表示边界点q在固定曲面上的位置。
[0049]
进一步地，所述步骤(5)中利用拉格朗日通量算法(lfc)对以下表达式进行求解，计算出时间段t0～t0 k内粒子穿过固定曲面的电通量i；
[0050][0051]
[0052]
其中：∧表示楔积(wedge product)运算符，f(x,y,z)为粒子浓度函数f(x,t0)在x方向上的积分，x＝(x,y,z)且(x,y,z)表示三维空间中任一点的坐标。
[0053]
进一步地，可采用以下公式对上述电通量i的积分表达式进行计算；
[0054][0055]
其中：表示由生成曲面上某一个点导出的三维坐标值，表示坐标点的浓度，表示在这个点的浓度权重，生成曲面被划分成l
×
l份，每一小份曲面上横纵各取n和m个点，即每一小份共有n
×
m个点，h为自定义的积分节点数。
[0056]
进一步地，所述固定曲面可表示为：
[0057][0058]
其中：u和v为三维空间中曲面的参数变量。
[0059]
本发明利用通量恒等式将欧拉通量积分转化为lfc有以下三点好处：
[0060]
1.lfc不需要在全局范围内求解标量守恒律方程，只需要在一个很小的局部范围内利用标量函数的初值计算积分即可。
[0061]
2.有时我们并不关注标量函数在整个计算域内的运动过程，而只关注浓度函数f在局部区域的运动状态；在这种情况下，lfc将会使fvm-mol更加的稳定和灵活。
[0062]
3.在计算标量守恒律时，lfc的好处是可以计算标量函数可积但不连续的情况，且时间步长不受cfl条件的限制。
[0063]
此外，对于三维数值的lfc算法，算法的时间区间可以任意的长，并且算法中避免了求曲线交点；且lfc算法实现简单，且具有高精度、高效率以及稳定性，还达到了二、四、六阶收敛率。
附图说明
[0064]
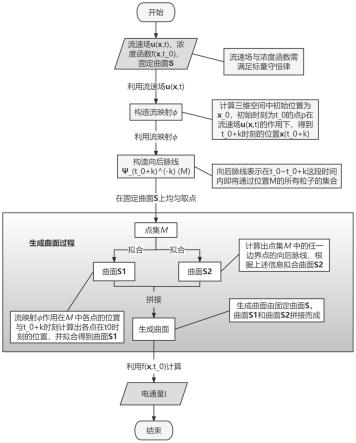
图1为本发明高精度电通量计算方法的步骤流程示意图。
具体实施方式
[0065]
为了更为具体地描述本发明，下面结合附图及具体实施方式对本发明的技术方案进行详细说明。
[0066]
如图1所示，本发明针对芯片制造过程中晶圆注入离子环节提出了一种高精度电通量计算方法，包括如下步骤：
[0067]
(1)首先确定三维空间中的流速场u(x,t)、初始时间粒子的浓度函数f(x,t0)以及固定曲面进而根据流速场u(x,t)构造一个流映射φ，利用流映射φ构造向后脉线其表示时间段t0～t0 k内通过位置m的所有粒子的集合。
[0068]
考虑非自治的常微分方程(ode)：
[0069][0070]
其中：当u(x,t)在时间上连续且在空间上lipschitz连续时，ode方程对给定初始时间和初始位置都存在唯一的解，由唯一性我们可以定义流映射，即：
[0071][0072]
其中：t0、x0、和k分别是初始时间、初始位置以及时间增量，x(t0 k)是ode方程在t0 k的解。
[0073]
对于一个给定的非定常流速场u(x,t)以及给定的初始条件x0,t0，流映射将在初始位置x0初始时刻t0的粒子映射到时刻t0 k的位置x(t0 k)上。事实上，我们对ode方程的两端进行时间积分，可以得到：
[0074][0075][0076]
其中：上标 ,-分别表示粒子在流映射作用下向前或向后的运动，若上标没有明确标注，表示可以向前也可以向后运动。
[0077]
我们记流映射作用在点m上的原像为这个记号同样可以用到一个点集上；当流映射作用在一个区域上时，有如下性质：
[0078]
给定初始时间t0，每个带有不同k的流映射之间是微分同胚的，即这里的流映射之间存在一个连续的双射函数。
[0079][0080]
一条开曲线是连续映射若γ是单射，则称这条开曲线为简单曲线；若γ(0)＝γ(1)，且映射是单射，那么这条开曲线就称为简单闭曲线，也叫约当曲线。
[0081]
粒子集的时间线，是这组粒子集在流映射的作用下，映射到相空间上的子集
[0082][0083]
其中：上标 ,-分别表示粒子向前或向后运动，同时也分别表示的像或原像。
[0084]
由以上可知，粒子集与它的像和原像均同胚，即：
[0085][0086]
定义向前脉线和向后脉线分别为：
[0087][0088]
和
[0089][0090]
其中：时间增量k》0。
[0091]
脉线是在某一时间间隔内相继经过空间中同一位置点的粒子依次串连而成的曲线。在生活中向前脉线更为常见，比如在流动的河水中滴下一滴墨水，墨水随即四散开来，形成不规划的曲线，这条曲线就是向前脉线；而向后脉线可以理解为将时间和河水的速度场逆转之后得到的曲线。
[0092]
向前脉线与向后脉线之间还有如下的关系：
[0093][0094]
当一条脉线相关联的时间间隔足够小时，这条脉线不会自交。
[0095]
当时间间隔足够小时，两条脉线是不会相交的。
[0096]
这两条引理说明，当时间间隔足够小时，脉线之间既不会自交也不会相交。因此，我们可以将一个时间区间分成足够小的时间区间的集合，使得在每个小时间区间内，脉线之间既不自交也不相交。在拉格朗日通量中，我们将用到的是向后脉线，而向前脉线只用于数学理论上的分析。
[0097]
(2)利用流映射φ、向后脉线和固定曲面构造生成曲面
[0098]
在拉格朗日通量的算法里主要用到了粒子集的时间线和脉线，本发明中我们主要考虑的是三维空间中的拉格朗日通量，因此有必要将曲线推广至曲面。
[0099]
参数曲面是指从的一个区域t(即中的一个连通开子集)到空间的一个连续映射设其中(u,v)∈t，则：
[0100]
γ:r＝r(u,v)
[0101]
设(u0,v0)∈t，若：
[0102][0103]
则称p0＝r(u0,v0)为曲面γ上的正则点，否则称为奇点；当γ上的所有点都是正则点时，称γ为正则曲面。这里ru×rv
|(u0,v0)当成γ在点p0处的一个法向量，可以看到，当曲面加上正则条件时，就保证了曲面处处存在着切平面和法向量。
[0104]
当参数(u,v)在t上连续变化时，法向量在γ上也连续的变化，而不会突然转到相反的方向上去，这时我们叫曲面γ是可定向的，正则曲面均是可定向的。
[0105][0106]
以上向量是正则曲面γ上的单位法向量，可以指定任意一个作为γ的正方向，而另一个则为负方向；当曲面的正方向确定之后，曲面的边界曲线也确定了方向。这个规定是，当一个人站在曲面的正侧沿边界的正向绕行时，曲面的内部在他的左侧，只有曲面的定
向和曲面边界的方向符合这一规则时，称他们是协调的。
[0107]
对于由分片正则曲面片拼接而成的拼接曲面的定向问题，为了给整个曲面定向，每个曲面片应该是可定向的。因为任何两块曲面片拼接，相接部分是各自曲面边界上的一部分，任何三块曲面片拼接，相接的只能是边界上的一个点。若两块曲面片拼接时，他们边界曲线的定向在公共边界上的定向正好相反，那么我们称这两块曲面片的定向是协调的。若拼接曲面的任意两个拼接的曲面片均是协调的，这时我们就说拼接曲面是可定向的，并且约定，把协调选择的各曲面片上的定向，当作拼接曲面的正向。
[0108]
假设我们给定一个正则可定向且有界的固定曲面该固定曲面的边界是若尔当曲线。给定在相空间上的速度场u(x,t)，时间区间[t0,t0 k]，取在固定曲面处的速度方向占比更大的一侧为固定曲面的正向，可以得到曲面的时间面为：
[0109][0110]
取曲面的边界对其边界上的每一点引出向后脉线，得到由边界组成的向后脉线簇为：
[0111][0112]
因为固定曲面是正则有界可定向的，其边界是若尔当曲线，由流映射的同胚性，也是有界可定向的曲面，且边界是若尔当曲线；对若尔当曲线上的每个点连续的做曲线，得到的曲线簇形成曲面，即也是曲面。
[0113]
生成曲面是由固定曲面的时间面由的边界组成的向后脉线簇三部分拼接而成的一个三维封闭的拼接曲面，其表达式如下：
[0114][0115]
为使拼接曲面的定向是协调的，当固定曲面的定向确定之后，曲面的时间面由边界组成的向后脉线簇也随之确定。具体是，固定曲面的正向为大部分曲面上的速度方向，故而固定曲面的正向应该是在由生成曲面围成的有界区域中由有界指向无界的法向量，其他曲面片也是如此定向。
[0116]
(3)利用浓度函数f(x,t0)和生成曲面计算时间段t0～t0 k内粒子穿过固定曲面的电通量i，即：
[0117][0118][0119]
本发明采用拉格朗日通量算法的最终目的是计算等式中三维的数值拉格朗日通量积分，因为这个积分是标量函数f(x,t0)在捐献区间上的积分，所以我们需要得到捐献区
间的边界，即生成曲面的近似，而生成曲面是由固定曲面是由固定曲面的时间面由的边界组成的向后脉线簇组成的三维封闭的拼接曲面，而这些曲线片的组成中还用到了流映射与向后脉线。因此，我们的算法主要由四个部分组成：数值近似流映射、向后脉线、生成曲面和数值拉格朗日通量计算。
[0120]
记s(u,v)＝{x(u,v),y(u,v),z(u,v)}为κ阶的张量样条函数，其中记s(u,v)＝{x(u,v),y(u,v),z(u,v)}为κ阶的张量样条函数，其中为张量样条函数s(u,v)的插值节点，假设与为p个点的高斯-勒让德积分公式的节点和权重系数，则对任意阶数≤q的多项式函数f(x,y,z)，有下面的代数积分公式成立：
[0121][0122]
ξ是一个固定的常数，上述积分是一种数值积分公式，是为了数值计算电通量i的，其中s是固定曲面，即可以写成：
[0123]
s(u,v)＝{x(u,v),y(u,v),z(u,v)}
[0124]
其中：u,v为三维空间中曲面的参数变量，为曲面s(u,v)上的一系列节点，表示p个高斯-勒让德积分公式的节点，数学上已给出定值；表示p个高斯-勒让德积分公式的权重系数，数学上已给出定值；表示三维空间中一个点的坐标系数，表示在这个点的浓度，表示在这个点的浓度权重，具体表达如下：
[0125][0126][0127][0128][0129]
其中：
[0130]
以上积分公式是一种数值计算积分的算法，是本实施方式中所采用的用来计算电通量的数值算法，本领域人员可以根据自己需求采用其它方法来计算电通量，即利用lfc算法可以选择其它数值计算积分的算法来求解电通量i的表达式，但采用以上积分公式计算
的话，效率更高。
[0131]
上述对实施例的描述是为便于本技术领域的普通技术人员能理解和应用本发明，熟悉本领域技术的人员显然可以容易地对上述实施例做出各种修改，并把在此说明的一般原理应用到其他实施例中而不必经过创造性的劳动。因此，本发明不限于上述实施例，本领域技术人员根据本发明的揭示，对于本发明做出的改进和修改都应该在本发明的保护范围之内。