基于贝塞尔函数分段积分的集成电路电磁仿真方法及系统与流程

1.本技术涉及集成电路电磁仿真技术领域，特别涉及基于贝塞尔函数分段积分的集成电路电磁仿真方法及系统。


背景技术：

2.集成电路工作时其多层版图上由于高速信号的传输，会形成高频交变电磁场，同时，为了提高电子设备的性能，缩小体积，降低成本，将晶体管与其他元器件以及线路都集成在一小块半导体基片上。为了实现更多的功能，超大规模集成电路有数十层到上百层结构，每层结构极其复杂，集成上百万甚至上千万晶体管，且具有多尺度结构，尺度范围从厘米级到目前最新的纳米级。为了保证集成电路能正常工作并实现事先设计的功能，需要首先保证集成电路的电源完整性和信号完整性，因此需要采用电磁场分析的手段对数十层、上百层的多尺度结构的集成电路的电源完整性和信号完整性进行精准的分析，这是超大规模集成电路电磁场分析的一大难题。
3.分析三维超大规模集成电路的电磁响应的传统方法是三维电磁场数值计算方法，例如三维有限元方法。采用传统数值计算方法计算三维超大规模集成电路的电磁响应时，通常在设置一定区域的截断误差后，将整个三维集成电路连同集成电路之外的有限区域确定为计算区域，然后对整个计算区域进行网格剖分，并计算整个计算区域的电磁场分布，进而计算出集成电路每层的电磁场分布、电流分布、指定端口的电流电压等电磁响应。然而，集成电路过孔、走线等特征尺寸为纳米级，整个集成电路的尺寸为厘米级，而根据截断误差确定的计算区域则为分米级、米级，对这样的多尺度空间进行统一的网格剖分再分析其空间电磁辐射，会产生数亿的网格和未知量，导致计算的硬件(内存)成本和cpu时间成本都过大。为此，可采用有限元法和矩量法相结合的方法计算三维大规模集成电路电磁响应。在三维大规模集成电路区域，采用有限元法；在集成电路之外的大范围区域，采用矩量法；有限元法和矩量法在集成电路与外部空间的界面相耦合。
4.由于矩量法只针对界面进行积分，因此就会减少大量的网格单元和未知量。但由于集成电路的尺度范围为纳米级到厘米级，直接对集成电路整体用有限元法求解本身会产生巨大的稀疏矩阵，且由于有限元法和矩量法进行耦合，使得形成的耦合矩阵在界面处为稠密矩阵，大大增加了整个稀疏矩阵的非零元数量和稀疏矩阵求解复杂度，使得计算时间仍然很长。为此，可以基于源产生的场的线性叠加性质，利用二维高斯积分的方法高精度求解复杂结构的集成电路版图上的交变电流在任意位置产生的场。
5.在利用并矢格林函数快速计算超大规模集成电路的电磁场问题时，所有超大规模集成电路复杂版图的电磁场计算都可以分解为最基本的点电流源对场点形成的场。在计算位于点电流源对位于场点形成的场的公式中，所有计算最为核心和难点在于计算贝塞尔积分。贝塞尔函数由于高振荡、慢衰减等特性，使得其积分的快速、高精度计算一直成为研究的热点问题。而目前在采用贝塞尔函数进行积分的过程中，计算时间较长，时间成本较高，但在快速发展的超大规模集成电路的电磁仿真中，计算时间是非常重要的，它决定了计算
效率，因此计算时间是目前急需解决的一个问题。


技术实现要素：

6.基于此，为了快速、高精度的对超大规模集成电路进行电磁仿真，本技术采用格林函数法基于点源形成的场进行叠加实现，进一步，在如何快速、高精度的计算格林函数中的贝塞尔积分时，本技术基于贝塞尔函数的高振荡、慢衰减的特性，提出采用以贝塞尔函数的零点作为分段积分的初始分段，在此基础上，根据每个分段积分的误差，自适应对每个分段积分进行再分段，从而实现基于精度控制的快速、高精度的自适应分段积分，以及降低积分的时间成本，本技术公开了以下技术方案。
7.一方面，提供了一种基于贝塞尔函数分段积分的集成电路电磁仿真系统，包括：
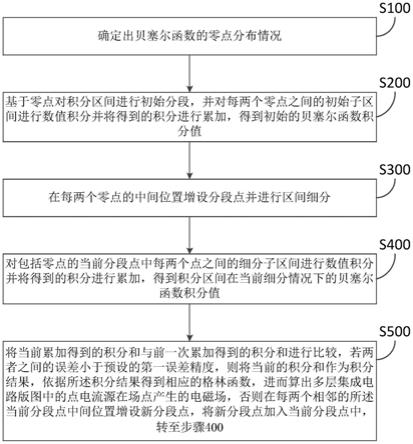
8.步骤100，确定出贝塞尔函数的零点分布情况；
9.步骤200，基于零点对积分区间进行初始分段，并对每两个零点之间的初始子区间进行数值积分并将得到的积分进行累加，得到初始的贝塞尔函数积分值；
10.步骤300，在每两个零点的中间位置增设分段点并进行区间细分；
11.步骤400，对包括零点的当前分段点中每两个点之间的细分子区间进行数值积分并将得到的积分进行累加，得到积分区间在当前细分情况下的贝塞尔函数积分值；
12.步骤500，将当前累加得到的积分和与前一次累加得到的积分和进行比较，若两者之间的误差小于预设的第一误差精度，则将当前的积分和作为积分结果，依据所述积分结果得到相应的格林函数，进而算出多层集成电路版图中的点电流源在场点产生的电磁场，否则在每两个相邻的所述当前分段点中间位置增设新分段点，将新分段点加入当前分段点中，转至步骤400。
13.在一种可能的实施方式中，步骤400中通过高斯积分方法来计算各子区间的积分，并通过下式计算各子区间的积分累加：
[0014][0015]
其中，g(r)为待积分的格林函数，r为格林函数作用的空间距离，为源点到待计算场点的距离；
[0016]
m为包括零点的当前分段点形成的细分子区间总数，k是高斯积分点总数；
[0017]
dm为每个子区间[λm，λ
m 1
]变换到标准高斯积分区间[-1,1]的雅可比变换，d
m-1
为dm的逆变换；
[0018]
xk是第k个高斯点，wk是第k个高斯点对应的权重；
[0019]
g(dm(xk))为函数g(λ)在λ取值为dm(xk)时的值，g(λ)为积分核函数，λ为积分变量；
[0020]jv
为v阶贝塞尔函数，v为贝塞尔函数的阶数。
[0021]
在一种可能的实施方式中，步骤500中，通过下式判断当前累加得到的积分和与前一次累加得到的积分和之间的误差是否小于第一误差精度η：
[0022]
|g
(j)
(r)-g
(j-1)
(r)|＜η
[0023]
其中，g
(j)
(r)表示积分子区间在当前第j次细分下的累加积分，g
(j-1)
(r)表示积分子区间在前一次第j-1次细分下的累加积分。
[0024]
在一种可能的实施方式中，依据下式(7)确定出零点个数的选择：
[0025][0026]
其中，表示未进行细分的情况下的第m个分段点，表示未进行细分的情况下的第m 1个分段点，ε为预设的第二误差精度。
[0027]
在一种可能的实施方式中，在步骤400中重新进行子区间的积分累加之后，在末位当前分段点和该分段点的后一分段点之间增设一个第二新分段点，若此时满足所述式(7)则完成对零点个数选择的确定，若此时未满足所述式(7)则执行以下步骤：
[0028]
步骤b1：设置q＝1；
[0029]
步骤b2：在当前细分的分段数量下计算积分：
[0030][0031]
步骤b3：将累加到g
(j 1)
(r)：
[0032][0033]
步骤b4：如果结束，否则设置q＝q 1,转入步骤b2；其中，
[0034]
表示未进行细分的情况下的第m q个分段点,对应贝塞尔函数jv(a)的第m q个零点，个零点，表示积分子区间在当前第j 1次细分情况下截断到贝塞尔函数jv(a)的第m q个零点后的累加积分。
[0035]
另一方面，还提供了一种基于贝塞尔函数分段积分的集成电路电磁仿真系统，包括：
[0036]
零点分布确定模块，用于确定出贝塞尔函数的零点分布情况；
[0037]
初始积分计算模块，用于基于零点对积分区间进行初始分段，并对每两个零点之间的初始子区间进行数值积分并将得到的积分进行累加，得到初始的贝塞尔函数积分值；
[0038]
区间细分模块，用于在每两个零点的中间位置增设分段点并进行区间细分；
[0039]
细分积分计算模块，用于对包括零点的当前分段点中每两个点之间的细分子区间进行数值积分并将得到的积分进行累加，得到积分区间在当前细分情况下的贝塞尔函数积分值；
[0040]
误差精度判断模块，用于将当前累加得到的积分和与前一次累加得到的积分和进行比较，若两者之间的误差小于预设的第一误差精度，则将当前的积分和作为积分结果，依据所述积分结果得到相应的格林函数，进而算出多层集成电路版图中的点电流源在场点产生的电磁场，否则在每两个相邻的所述当前分段点中间位置增设新分段点，将新分段点加
入当前分段点中，并使细分积分计算模块重新进行数值积分和积分累加，直到所述比较的误差小于所述第一误差精度。
[0041]
在一种可能的实施方式中，所述细分积分计算模块通过高斯积分方法来计算各子区间的积分，并通过下式计算各子区间的积分累加：
[0042][0043]
其中，g(r)为待积分的格林函数，r为格林函数作用的空间距离，为源点到待计算场点的距离；
[0044]
m为包括零点的当前分段点形成的细分子区间总数，k是高斯积分点总数；
[0045]
dm为每个子区间[λm，λ
m 1
]变换到标准高斯积分区间[-1,1]的雅可比变换，d
m-1
为dm的逆变换；
[0046]
xk是第k个高斯点，wk是第k个高斯点对应的权重；
[0047]
g(dm(xk))为函数g(λ)在λ取值为dm(xk)时的值，g(λ)为积分核函数，λ为积分变量；
[0048]jv
为v阶贝塞尔函数，v为贝塞尔函数的阶数。
[0049]
在一种可能的实施方式中，所述误差精度判断模块通过下式判断当前累加得到的积分和与前一次累加得到的积分和之间的误差是否小于第一误差精度η：
[0050]
|g
(j)
(r)-g
(j-1)
(r)|＜η
[0051]
其中，g
(j)
(r)表示积分子区间在当前第j次细分下的累加积分，g
(j-1)
(r)表示积分子区间在前一次第j-1次细分下的累加积分。
[0052]
在一种可能的实施方式中，依据下式(7)确定出零点个数的选择：
[0053][0054]
其中，表示未进行细分的情况下的第m个分段点，表示未进行细分的情况下的第m 1个分段点，ε为预设的第二误差精度。
[0055]
在一种可能的实施方式中，所述细分积分计算模块在重新进行子区间的积分累加之后，在末位当前分段点和该分段点的后一分段点之间增设一个第二新分段点，若此时满足所述式(7)则完成对零点个数选择的确定，若此时未满足所述式(7)则所述细分积分计算模块执行以下步骤：
[0056]
步骤b1：设置q＝1；
[0057]
步骤b2：在当前细分的分段数量下计算积分：
[0058][0059]
步骤b3：将累加到g
(j 1)
(r)：
[0060][0061]
步骤b4：如果结束，否则设置q＝q 1,转入步骤b2；其中，
[0062]
表示未进行细分的情况下的第m q个分段点,对应贝塞尔函数jv(a)的第m q个零点，个零点，表示积分子区间在当前第j 1次细分情况下截断到贝塞尔函数jv(a)的第m q个零点后的累加积分。
[0063]
本实施例公开的基于贝塞尔函数分段积分的集成电路电磁仿真方法及系统，针对贝塞尔函数高振荡、慢衰减的特点，本技术不直接对原始的贝塞尔函数的积分进行变换然后通过高斯积分法计算，而是将积分区间根据贝塞尔函数的零点进行分割，形成一系列的子区间，将原始的0到∞的积分分成多个子区间的积分的叠加，使得每个子区间的贝塞尔函数不再存在震荡的问题，对每个子区间，再将其变换到标准的[-1,1]的积分区间，然后采用高斯积分法进行计算，由此实现采用自适应零点分段来根据误差分析决定积分区间的分割，确保计算结果准确，实现了在满足精度要求时以自适应方式确定出相应的零点数量，利用阈值提高了零点之间积分结果的准确性。
附图说明
[0064]
以下参考附图描述的实施例是示例性的，旨在用于解释和说明本技术，而不能理解为对本技术的保护范围的限制。
[0065]
图1是本技术公开的基于贝塞尔函数分段积分的集成电路电磁仿真方法实施例的流程示意图。
[0066]
图2是贝塞尔函数零点和分段点的区间细分图。
[0067]
图3是本技术公开的基于贝塞尔函数分段积分的集成电路电磁仿真系统实施例的结构框图。
具体实施方式
[0068]
为使本技术实施的目的、技术方案和优点更加清楚，下面将结合本技术实施例中的附图，对本技术实施例中的技术方案进行更加详细的描述。
[0069]
下面参考图1-图2详细描述本技术公开的基于贝塞尔函数分段积分的集成电路电磁仿真方法方法实施例。
[0070]
以利用并矢格林函数快速计算超大规模集成电路电磁场的场景为例来说明本实施例公开的集成电路电磁仿真方法具体如何应用。首先，基于并矢格林函数计算点电流源在空间任意位置产生的场，然后基于源产生的场的线性叠加性质并利用二维高斯积分计算面电流源在相同位置产生的场，进而计算出复杂的不规则形状的集成电路版图形成的面电流源在相同位置产生的场。设整个集成电路共有多层，各层编号为l＝0,1,2,
…
，则位于源点坐标(x
t
，y
t
，z
t
)的点电流源对位于(x,y,z)的场点形成的场可用格林函数)的点电流源对位于(x,y,z)的场点形成的场可用格林函数和来表示，例如其中的
具体为：
[0071][0072]
而上述每个格林函数均各自包含一种或多种贝塞尔函数积分，例如中：
[0073][0074][0075]
等等。
[0076]
其中，t为虚数单位，t2＝-1，λ为积分变量，ω为电磁波的角频率，；表示第l层水平方向的复波数，表示第l层垂直方向的复波数，μ
h，l
表示第l层的水平方向的磁导率，μ
s，l
表示第l层的垂直方向的磁导率，ε
h，l
表示第l层的水平方向的介电常数，ε
s，l
表示第l层的垂直方向的介电常数；
[0077]
表示第l层水平方向的复波数的积分系数，表示第l层垂直方向的复波数的积分系数；
[0078]cl
、d
l
、e
l
和f
l
均表示第l层的待定系数；
[0079]
表示第l层的各向异性系数；z
l
为第l层分界面的z坐标；j0表示0阶贝塞尔函数；表示为贝塞尔积分系数，
[0080]
而格林函数中除了贝塞尔函数积分以外的部分为一些常量或者易于获取到、计算出的变量，因此可知，所有计算最为核心和难点在于计算格林函数中的贝塞尔积分，本实施例即可以在该场景下对贝塞尔函数积分计算进行具体展开。
[0081]
如图1所示，本实施例公开的方法包括如下步骤100至步骤500。
[0082]
步骤100，确定出贝塞尔函数的零点分布情况。
[0083]
对于贝塞尔函数积分，其一般具有以下形式：
[0084][0085]
式(1)中，g(r)为待积分的格林函数，r为格林函数作用的空间距离，为源点到待计算场点的距离；g(λ)为积分核函数，jv为v阶贝塞尔函数，v为贝塞尔函数的阶数，λ为积分变量。
[0086]
贝塞尔函数的零点a是贝塞尔函数值为0的解，即jv(a)＝0的解，具体可以通过以下halley算法计算得出。
[0087]
步骤a1，设置i＝1。
[0088]
步骤a2，设定第i个零点的初始猜测值
[0089]
步骤a3，通过以下迭代公式计算附近的贝塞尔函数jv(a)的第i个零点：
[0090][0091]
迭代终止条件：其中δ为预先定义的阈值。其中，j
′v表示贝塞尔函数jv的一阶导数，j
″v表示贝塞尔函数jv的二阶导数；n表示第n轮迭代，n＝0时的值为初始猜测值。
[0092]
步骤a4，如果计算的零点达到指定的区间范围，则完成计算；否则，使i＝i 1,并转入步骤a2。
[0093]
根据贝塞尔函数的零点，即可确定基于贝塞尔函数的零点获得的形成积分区间的分段点为其中，积分区间相当于积分变量的取值范围。
[0094]
步骤200，基于零点对积分区间进行初始分段，并对每两个零点之间的初始子区间进行数值积分并将得到的积分进行累加，得到初始的贝塞尔函数积分值。
[0095]
基于零点对积分区间进行分段，得到图2中的其中上标指的是积分区间的细分次数，当前未进行细分所以是0，下标是零点的序号。可以理解的是，图2中仅以5个零点为例进行说明，实际的零点数量根据贝塞尔函数的零点分布情况而定。需要说明的是，积分是针对λ的积分，分段是针对λ的积分区间进行分段，分段的点为这样在所有分段点λi，rλi都为贝塞尔函数的零点。
[0096]
此时，根据贝塞尔函数的零点将整个积分区间分成若干个初始子区间，相应的整个积分式(1)也分解为若干个初始子区间积分的累加，然后分别对每个初始子区间用数值积分方法进行计算并累加，例如可以采用高斯积分进行计算和累加，得到以零点划分区间时对应的贝塞尔函数积分值。
[0097]
步骤300，在每两个零点的中间位置增设分段点并进行区间细分。
[0098]
本次的当前分段点为因为已经开启了分段区间细分的过程，因此所有零点和当前分段点的上标变为1，但零点的位置未产生变化，而当前分段点则位于每两个零点的正中间位置，经过将所有零点和当前分段点进行重新排序使得序号大小与点的顺位相匹配后，确定出零点的指代符号变为分别对应之前的可以理解的是，这里的“细分”仅表示在原始分段点的基础上新增加分段点对积分区域进行再分段，因此“细分”是区别于步骤200中的基于零点对积分区间进行初始分段的。
[0099]
此时，根据新增的分段点，将由零点划分出的初始子区间进行了进一步细分，由原来的4个初始子区间变为了8个分段子区间。可以理解的是，若方法运行过程中发现还需进行再次细分，则之后的分段点均位于零点与分段点之间以及分段点与分段点之间了，如图2中的等。
[0100]
步骤400，对包括零点的当前分段点中每两个点之间的细分子区间进行数值积分并将得到的积分进行累加，得到积分区间在当前细分情况下的贝塞尔函数积分值。
[0101]
分别对每个细分子区间用数值积分方法进行计算并累加，得到包括零点在内的当前分段点划分区间时对应的贝塞尔函数积分值。在根据当前分段点将整个积分区间分成若干个细分子区间的情况下，式(1)可写为下式(2)：
[0102][0103]
式(2)中，m为包括零点的当前分段点形成的细分子区间总数，λm为贝塞尔函数的第m个分段点。
[0104]
在λ
m 1
足够大时，有下式(3)：
[0105][0106]
由式(2)和式(3)可得式(4)：
[0107][0108]
在一种实施方式中，可以通过高斯积分方法来计算式(4)中的各子区间的积分，从而通过下式(5)来计算各子区间的积分累加：
[0109][0110]
式(5)中，k是高斯积分点总数；dm为每个子区间[λm，λ
m 1
]变换到标准高斯积分区间[-1,1]的雅可比变换，d
m-1
为dm的逆变换，且设λ0＝0；xk是第k个高斯点，wk是第k个高斯点
对应的权重；g(dm(xk))为函数g(λ)在λ取值为dm(xk)时的值。
[0111]
式(5)算出的结果即为当前分段点下的积分结果，在还未进行分段点增设并开启细分时，也就是步骤200时，积分结果记为g
(0)
(r)，其中的上标表示积分子区间细分次数，上标为0表示积分区间直接依据贝塞尔函数的零点进行划分，零点之间未进行细分，步骤300及以后时，积分结果记为g
(j)
(r)，j为积分子区间细分次数且j》0。
[0112]
步骤500，将当前累加得到的积分和与前一次累加得到的积分和进行比较，若两者之间的误差小于预设的第一误差精度η，则将当前的积分和作为积分结果，依据所述积分结果得到相应的格林函数，进而算出多层集成电路版图中的点电流源在场点产生的电磁场，否则在每两个相邻的所述当前分段点中间位置增设新分段点，将新分段点加入当前分段点中，转至步骤400。
[0113]
第一误差精度为一个预设值，用于判断当前细分次数下得到的积分结果是否已经足够趋近于准确值，若已经足够趋近于准确值，则说明当前细分次数下的当前分段点及其分割出的子区间已经能够保证积分计算结果的准确性，因此可以结束分段，并将当前细分次数下的积分结果作为最终的准确积分结果。
[0114]
在一种实施方式中，可以通过下式(6)判断当前累加得到的积分和与前一次累加得到的积分和之间的误差是否小于第一误差精度η，同时依据下式(7)确定出零点个数的选择：
[0115]
|g
(j)
(r)-g
(j-1)
(r)|＜η
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)；
[0116][0117]
上式(6)中，g
(j)
(r)表示积分子区间在当前第j次细分下的累加积分，g
(j-1)
(r)表示积分子区间在前一次第j-1次细分下的累加积分。
[0118]
上式(7)中，表示未进行细分的情况下的第m个分段点，表示未进行细分的情况下的第m 1个分段点。
[0119]
需要注意的是，式(7)计算的积分本身有可能是不准确的，其积分值随着这个积分子区间的细分次数的变化而变化，也就是说，如果在子区间未细分情况下计算出来的积分值满足式(7)，但在子区间细分为两段情况下计算出来的积分值不再满足式(7)，则此时需要继续增加式(5)中的m的值到m n，直到当前分段数量情况下新的m’＝m n值满足式(7),即：
[0120][0121]
其中，ε为预设的第二误差精度，一般取当前数据类型下的机器精度，例如采用双精度数据计算，则是双精度数据下的机器精度；为未进行细分的情况下的第m’个分段点。
[0122]
若满足式(7)，则可以忽略λm′
1
之后的所有贝塞尔零点，即可认为：
[0123][0124]
若当前细分次数下得到的积分结果未能足够趋近于准确值，则说明当前细分次数下的当前分段点及其分割出的子区间还不能够保证积分计算结果的准确性，需要对前一次细分后的子区间进行再次细分，也就是本次还需要继续细分并在前一次细分时采用的分段点之间增设新的分段点，使得能够基于更多数量的分段点对积分区间进行更为细粒度的划分，以将积分区间分割为更多数量的子区间，然后再代入步骤400中，实现步骤400-500之间的循环，并在每次细分后基于当前的细分次数，通过计算式(7)判断是否更新需要的贝塞尔零点个数，直到某一次迭代后判定出误差小于第一误差精度了，此时结束分段，并将本次的步骤400-》500循环中步骤400计算出的积分结果作为最终的准确积分结果。
[0125]
由此，针对在贝塞尔函数的两个零点之间只分一个区间再用高斯积分法进行积分的结果并不准确的问题，在贝塞尔函数的零点间划分更细的区间，并通过误差对区间细分段数进行自适应控制，实现了在两个零点之间进行自适应分段直到精度满足要求为止。
[0126]
在一种实施方式中，所述在每两个相邻的所述当前分段点之间增设新分段点，将新分段点加入当前分段点中，具体包括：在每两个当前分段点的中间位置增设一个新分段点，并将所有的分段点按从小到大的顺序重新编号。
[0127]
假设当前处于未进行细分的情况，此时的当前分段点全部对应为零点，也就是图2中的若此时在步骤500中判断出误差不满足误差精度要求η，则中的每两个零点的中间位置新增一个分段点，称为第一新分段点，第一新分段点可通过下式(10)表达：
[0128][0129]
此时前一次的细分次数j＝0，新的细分次数为j 1＝1，new1、new2等为新分段点在未进行重新编号之前的序号。此时的新分段点共有5-1＝4个，将其加入当前分段点后，当前分段点共有4 5＝9个，经按从小到大重新编号后，得到图2中的并且如图中箭头所示，与对应，与对应，依此类推，此时第一新分段点包括：以及
[0130]
将该9个当前分段点代入步骤400重新进行分段后的子区间积分累加，然后在最后一个当前分段点和该当前分段点的后一个贝塞尔零点对应的分段点之间也新
插入一个细分点也就是增设一个第二新分段点。其中是依据步骤100中得到的零点分布情况中排在之后的零点对应的分段点，重新计算式(7)所示的积分发现此时式(7)仍然满足，则细分子区间个数m＝5不变，此时完成了零点个数的确定。然后对积分累加值进行误差判断，也就是判断当前累加得到的积分和与前一次累加得到的积分和之间的误差是否小于误差精度η，若还未满足误差精度要求，则再次按式(10)进行分段，此时前一次的细分次数j＝1，而新的细分次数为j 1＝2，得到图2中的并且如图中箭头所示，与对应，与对应，依此类推。
[0131]
在当前细分的分段数量下，重新按当前细分对积分区间进行分段，计算当前细分是否满足式(7)，如果再次计算的该积分不再满足式(7)则进行以下步骤：
[0132]
步骤b1：设置q＝1；
[0133]
步骤b2：在当前细分的分段数量下计算积分：
[0134][0135]
步骤b3：将累加到g
(j 1)
(r)：
[0136][0137]
步骤b4：如果结束，否则设置q＝q 1,转入步骤b2。
[0138]
以上式中,表示未进行细分的情况下的第m q个分段点,对应贝塞尔函数jv(a)的第m q个零点，(a)的第m q个零点，表示积分子区间在当前第j 1次细分情况下截断到贝塞尔函数jv(a)的第m q个零点后的累加积分。
[0139]
按上述方式对积分区间进行细分分段，直到某次细分时在步骤500处判断出满足误差精度，且在当前细分次数下同时满足式(7)，此时停止继续细分，并将在当前分段和子区间下的积分累加数值作为最终的积分结果。
[0140]
在计算试验过程中发现，用于集成电路电磁场计算的格林函数方法，其中采用的0阶和1阶贝塞尔函数具有高振荡、慢衰减等特性，且由于集成电路的最小尺度达纳米级，因此计算集成电路电磁场的格林函数作用的空间距离最小尺度也达纳米级，而最大尺度则依据计算的问题不同而不同，例如计算集成电路不同层之间的耦合，其作用的空间距离为集成电路的最大尺寸，为厘米级，如果计算集成电路对空间的电磁辐射，纳米作用的空间距离则为空间电磁辐射的考虑范围，达米级，由此可见，用于集成电路电磁场计算的格林函数作用的空间距离涵盖了从纳米级到米级的多尺度范围，这样大的尺度范围使得直接对原始的贝塞尔函数的积分做变换然后通过高斯积分法计算结果不正确。
[0141]
基于此，本实施例的意义在于，针对贝塞尔函数高振荡、慢衰减的特点，本技术不直接对原始的贝塞尔函数的积分进行变换然后通过高斯积分法计算，而是将积分区间根据贝塞尔函数的零点进行分割，形成一系列的子区间，将原始的0到∞的积分分成多个子区间的积分的叠加，使得每个子区间的贝塞尔函数不再存在震荡的问题，对每个子区间，再将其变换到标准的[-1,1]的积分区间，然后采用高斯积分法进行计算，由此实现采用自适应零点分段来根据误差分析决定积分区间的分割，确保计算结果准确，实现了在满足精度要求时以自适应方式确定出相应的零点数量，利用阈值提高了零点之间积分结果的准确性。
[0142]
下面参考图3详细描述本技术公开的基于贝塞尔函数分段积分的集成电路电磁仿真系统实施例。本实施例是用于实施前述的集成电路电磁仿真方法实施例的系统。
[0143]
如图3所示，本实施例公开的集成电路电磁仿真系统，包括：零点分布确定模块、初始积分计算模块、区间细分模块、细分积分计算模块和误差精度判断模块。
[0144]
零点分布确定模块用于确定出贝塞尔函数的零点分布情况。
[0145]
初始积分计算模块用于基于零点对积分区间进行初始分段，并对每两个零点之间的初始子区间进行数值积分并将得到的积分进行累加，得到初始的贝塞尔函数积分值。
[0146]
区间细分模块用于在每两个零点的中间位置增设分段点并进行区间细分。
[0147]
细分积分计算模块用于对包括零点的当前分段点中每两个点之间的细分子区间进行数值积分并将得到的积分进行累加，得到积分区间在当前细分情况下的贝塞尔函数积分值。
[0148]
误差精度判断模块用于将当前累加得到的积分和与前一次累加得到的积分和进行比较，若两者之间的误差小于预设的第一误差精度，则将当前的积分和作为积分结果，依据所述积分结果得到相应的格林函数，进而算出多层集成电路版图中的点电流源在场点产生的电磁场，否则在每两个相邻的所述当前分段点中间位置增设新分段点，将新分段点加入当前分段点中，并使细分积分计算模块重新进行数值积分和积分累加，直到所述比较的误差小于所述第一误差精度。
[0149]
在一种实施方式中，所述细分积分计算模块通过高斯积分方法来计算各子区间的积分，并通过下式计算各子区间的积分累加：
[0150][0151]
其中，g(r)为待积分的格林函数，r为格林函数作用的空间距离，为源点到待计算场点的距离；
[0152]
m为包括零点的当前分段点形成的细分子区间总数，k是高斯积分点总数；
[0153]
dm为每个子区间[λm，λ
m 1
]变换到标准高斯积分区间[-1,1]的雅可比变换，d
m-1
为dm的逆变换；
[0154]
xk是第k个高斯点，wk是第k个高斯点对应的权重；
[0155]
g(dm(xk))为函数g(λ)在λ取值为dm(xk)时的值，g(λ)为积分核函数，λ为积分变量；
[0156]jv
为v阶贝塞尔函数，v为贝塞尔函数的阶数。
[0157]
在一种实施方式中，所述误差精度判断模块通过下式判断当前累加得到的积分和与前一次累加得到的积分和之间的误差是否小于第一误差精度η：
[0158]
|g
(j)
(r)-g
(j-1)
(r)|＜η
[0159]
其中，g
(j)
(r)表示积分子区间在当前第j次细分下的累加积分，g
(j-1)
(r)表示积分子区间在前一次第j-1次细分下的累加积分。
[0160]
在一种实施方式中，依据下式(7)确定出零点个数的选择：
[0161][0162]
其中，表示未进行细分的情况下的第m个分段点，表示未进行细分的情况下的第m 1个分段点，ε为预设的第二误差精度。
[0163]
在一种实施方式中，所述细分积分计算模块在重新进行子区间的积分累加之后，在末位当前分段点和该分段点的后一分段点之间增设一个第二新分段点，若此时满足所述式(7)则完成对零点个数选择的确定，若此时未满足所述式(7)则所述细分积分计算模块执行以下步骤：
[0164]
步骤b1：设置q＝1；
[0165]
步骤b2：在当前细分的分段数量下计算积分：
[0166][0167]
步骤b3：将累加到g
(j-1)
(r)：
[0168][0169]
步骤b4：如果结束，否则设置q＝q 1,转入步骤b2；
[0170]
其中，
[0171]
表示未进行细分的情况下的第m q个分段点,对应贝塞尔函数jv(a)的第m q个零点，个零点，表示积分子区间在当前第j 1次细分情况下截断到贝塞尔函数jv(a)的第m q个零点后的累加积分。
[0172]
本文中的模块、单元或组件的划分仅仅是一种逻辑功能的划分，在实际实现时可以有其他的划分方式，例如多个模块和/或单元可以结合或集成于另一个系统中。作为分离部件说明的模块、单元、组件在物理上可以是分开的，也可以是不分开的。作为单元显示的部件可以是物理单元，也可以不是物理单元，即可以位于一个具体地方，也可以分布到网格单元中。因此可以根据实际需要选择其中的部分或全部的单元来实现实施例的方案。
[0173]
以上所述，仅为本技术的具体实施方式，但本技术的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本技术揭露的技术范围内，可轻易想到的变化或替换，都应涵盖在本技术的保护范围之内。因此，本技术的保护范围应以所述权利要求的保护范围为准。