一种非线性奇异摄动微分方程的神经网络计算方法与流程

1.本发明涉及工程领域、气体动力学、化学反应、流体力学和弹性力学奇异摄动模型求解技术领域，尤其涉及一种非线性奇异摄动微分方程的神经网络计算方法。


背景技术：

2.目前，渐近展开方法和数值方法是研究非线性奇异摄动微分方程的两大方法。渐近展开方法包括匹配渐近展开法、边界层函数方法、伸展合成法、微分不等式法和多尺度法等。数值求解方法包括有限差分法、有限元法，变分法、有理谱配点法、层适应网格法和自适应网格法等。
3.但是以上算法要求小步长计算才能达到较好的精度，计算工作量较大；
4.在求解工程领域、气体动力学、化学反应、流体力学和弹性力学等领域的问题时经常会转化成含有小参数的奇异摄动模型的求解，但由于参数很小，在运用以上算法求近似解的时候，计算工作量较大，且存在对于复杂模型往往无法逼近的问题。


技术实现要素：

5.本发明的目的是提供一种非线性奇异摄动微分方程的神经网络计算方法，旨在解决现有技术中，在求解工程领域、气体动力学、化学反应、流体力学和弹性力学等领域的问题时计算工作量较大、求解时间较长、精度较低的问题。
6.本发明实施例提供了一种非线性奇异摄动微分方程的神经网络计算方法，包括：
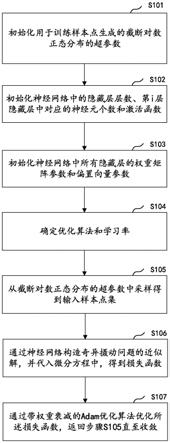
7.s101：初始化用于训练样本点生成的截断对数正态分布的超参数，记为tlogn(μ，σ
，
a，b)；
8.s102：初始化神经网络中的隐藏层层数h、第i层隐藏层中对应的神经元个数ni和激活函数σ(x)；
9.s103：初始化神经网络中所有隐藏层的权重矩阵参数和偏置向量参数，记为参数向量θ；
10.s104：确定优化算法和学习率η；
11.s105：从tlogn(μ，σ，a，b)中采样得到输入样本点集{xi，i＝1，
…
，n}；
12.s106：通过神经网络构造奇异摄动问题的近似解，并代入微分方程中，得到损失函数；
13.s107：通过带权重衰减的adam优化算法优化所述损失函数，返回步骤s105直至收敛。
14.本发明实施例针对非线性奇异摄动方程解的边界层特性，引入了截断对数正态分布采样的方法构造样本点，使得奇异摄动问题的先验信息得到了充分利用，相比传统方法在求解时间和精度上都得到了不同程度的提升，且针对一些传统方法无法求解的复杂问题，都可以求解。
附图说明
15.为了更清楚地说明本发明实施例技术方案，下面将对实施例描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
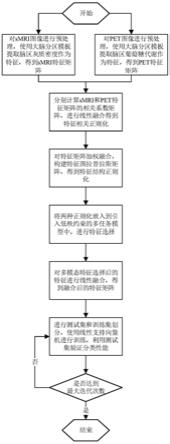
16.图1为本发明实施例提供的非线性奇异摄动微分方程的神经网络计算方法的流程示意图；
17.图2为本发明实施例提供的在保持期望不变(μ＝0)时，不同方差的对数正态分布的概率密度函数曲线；
18.图3为本发明实施例提供的在保持期望不变(μ＝0)时，不同方差的对数正态分布的累积分布函数曲线。
具体实施方式
19.下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
20.应当理解，当在本说明书和所附权利要求书中使用时，术语“包括”和“包含”指示所描述特征、整体、步骤、操作、元素和/或组件的存在，但并不排除一个或多个其它特征、整体、步骤、操作、元素、组件和/或其集合的存在或添加。
21.还应当理解，在此本发明说明书中所使用的术语仅仅是出于描述特定实施例的目的而并不意在限制本发明。如在本发明说明书和所附权利要求书中所使用的那样，除非上下文清楚地指明其它情况，否则单数形式的“一”、“一个”及“该”意在包括复数形式。
22.还应当进一步理解，在本发明说明书和所附权利要求书中使用的术语“和/或”是指相关联列出的项中的一个或多个的任何组合以及所有可能组合，并且包括这些组合。
23.请参阅图1，一种非线性奇异摄动微分方程的神经网络计算方法，包括：
24.s101：初始化用于训练样本点生成的截断对数正态分布的超参数，记为tlogn(μ，σ，a，b)；
25.s102：初始化神经网络中的隐藏层层数h、第i层隐藏层中对应的神经元个数ni和激活函数σ(x)；
26.s103：初始化神经网络中所有隐藏层的权重矩阵参数和偏置向量参数，记为参数向量θ；
27.s104：确定优化算法和学习率η；
28.s105：从tlogn(μ，σ，a，b)中采样得到输入样本点集{xi，i＝1，
…
，n}；
29.s106：通过神经网络构造奇异摄动问题的近似解，并代入微分方程中，得到损失函数；
30.s107：通过带权重衰减的adam优化算法优化所述损失函数，返回步骤s105直至收敛。
31.在本实施例中，率先对各模型和参数进行初始化，针对非线性奇异摄动方程解的边界层特性，引入了截断对数正态分布采样的方法构造样本点，使得奇异摄动问题的先验
信息得到了充分利用，相比传统方法在求解时间和精度上都得到了不同程度的提升，且针对一些传统方法无法求解的复杂问题，都可以求解。
32.其中，步骤s104中，对现有优化算法进行逐一尝试，取优化效果最好的一优化算法，并确定相应的学习率；
33.具体的，本技术中取用adam优化算法。
34.在一实施例中，所述从tlogn(μ，σ，a，b)中采样得到输入样本点集{xi，i＝1，
…
，n}，包括：
35.s201：采用以下公式计算所述对数正态分布的概率密度函数：
[0036][0037]
s202：采用以下公式计算所述对数正态分布的累积分布函数：
[0038][0039]
s203：根据所求问题的定义域区间对所述对数正态分布进行截断；
[0040]
s204：在截断后的对数正态分布上采样得到用于每轮迭代的样本点；
[0041]
其中，μ和σ为对数正态分布的期望和方差，φ和分别为标准正态分布n(0，1)的累积分布函数和概率密度函数；
[0042][0043]
在本实施例中，从损失函数中估计参数向量θ非常困难，由于要求由多层神经网络生成的高度非线性非凸函数在连续域i上的积分之计算复杂度非常高，所以一般采用随机采样的方式生成神经网络的训练样本点。
[0044]
在大多数情况下，使用随机均匀采样方法效果很好，但对于某些具有陡峭梯度的微分方程来说，使用均匀分布的样本点求解效率可能不高。从直觉上讲，应该在快变的部分放置更多点，以便很好地学习到弱连续的部分。但是，要为未知解的问题设计一个好的样本点分布是有挑战性的。
[0045]
对一些实际应用中的微分方程问题，通常只想知道狭窄位置或者说快变区间内的解，那么当使用神经网络求解这类问题时，一般使用类似于求解微分方程的经典方法，在感兴趣区域周围采样更多的点，实验结果表明该方法相比均匀网格确实更有效。
[0046]
针对非线性奇异摄动问题的求解，在生成每轮迭代所使用样本的时候依特定的概率分布，该概率分布需要满足在奇异摄动问题的快变区间内有很大的峰度且期望在快变区间内。
[0047]
经试验发现，对奇异摄动问题的求解适合使用截断的对数正态分布进行采样。
[0048]
具体的，关于截断对数正态分布：
[0049]
在概率论与统计学中，若随机变量的对数服从正态分布，则这个随机变量服从的分布称为对数正态分布.即如果ln(x)服从正态分布，则x服从对数正态分布。若令φ和分别为标准正态分布n(0，1)的累积分布函数和概率密度函数，那么对应的对数正态分布的概率密度函数为
[0050][0051]
对应的对数正态分布的累积分布函数为
[0052][0053]
其中μ和σ为对数正态分布的期望和方差，控制分布的形态。
[0054]
请参考图2-3，可以看到，随着方差逐渐增大，概率密度曲线也逐渐偏向0点，且峰度也越来越高，如σ＝10时的概率密度曲线。当方差变小时，概率密度的峰值向1靠近，累计分布函数曲线在x＝1的斜率也逐渐变大。对数正态分布的这种性质恰好符合奇异摄动问题求解过程中对样本点的要求。只需要根据所求问题的定义域区间对对数正态分布进行截断，然后在截断后的对数正态分布(truncated log-normal distribution)上采样得到用于每轮迭代的样本点。
[0055]
在一实施例中，所述奇异摄动问题，包括：
[0056]
一阶非线性奇异摄动初值问题：
[0057]
[0058]
二阶非线性奇异摄动边值问题：
[0059][0060]
其中，∈是摄动参数，y(x)∈rn是连续可导的函数，f(x，y)是关于的非线性且连续光滑的映射，c∈rn是y在x＝a处的初值，f(x，y，y
′
)是关于y和y
′
的非线性且连续光滑的映射，a∈rn和b∈rn分别是y在x＝a和x＝b处的边值。
[0061]
在一实施例中，所述通过神经网络构造奇异摄动问题的近似解，并代入微分方程中，得到损失函数，包括：
[0062]
s401：采用以下公式定义包含个隐藏层的全连接神经网络：
[0063][0064]
s402：使用神经网络nn(x；θi)构造奇异摄动问题的近似解ya(x)，并通过改变神经网络的参数使得对于阈值ε，满足以下公式：
[0065][0066]
s403：将近似解ya(x)记为并令
[0067]
s404：结合奇异摄动问题和神经网络，采用以下公式计算损失函数：
[0068][0069]
其中，∈是摄动参数，为离散集合，i为连续域，σ为某种非线性激活函数，n
in
和n
out
分别为输入和输出的维度，ni为第i个隐藏层的输出维度，同时也是该层的神经元个数，和分别为第i层的权重矩阵和偏置向量，θi为所有wj，bj(j≤i)的集合，即前面i-1层的所有参数，nni(x；θi)为第i层网络的输出。
[0070]
在本实施例中，
[0071][0072]
函数是将神经网络近似解代入奇异摄动问题，然后对微分方程以及初边值条件等式两边的项求损失j(θ)的二范数，其大小可以直接反映出近似解的精确程度，当j(θ)＝0时，则为该方程的解析解。因此，通过优化损失函数j(θ)得到最优参数向量
其对应的神经网络可以作为微分方程的近似解析解。
[0073]
在一实施例中，为了方便计算并优化损失函数公式，所述通过神经网络构造奇异摄动问题的近似解，并代入微分方程中，得到损失函数，包括：
[0074]
s501：将j(θ)的第一项通过以下公式替代：
[0075][0076]
s502：将e(θ)在定义域i中采样无穷多的点并累加得到以下公式：
[0077][0078]
s503：结合s502和s404，采用以下公式改写损失函数：
[0079][0080]
其中，s(i)为在定义域内采样得到的点，为初始点或边界点集。
[0081]
在本实施例中，对所求解的问题而言，为离散集合，第二项的值可直接算出；
[0082]
定义域i为连续域，故第一项的值需要在方程的整个定义域上积分才能求得。由于神经网络是很多层网络之间的非线性加线性叠加运算，所以对这样的函数做积分预算的难度是很大的，故将j(θ)的第一项通过以下公式替代：
[0083][0084]
若在定义域内采样无穷多的点并累加，可以任意精度来逼近定积分的真值，即e(θ)满足：
[0085][0086]
上式表明，假设通过优化算法足够强大，可以找到损失函数的最优解，且不考虑算力限制，那么我们可以通过在定义域内采样足够多的点来无限逼近损失函数最小值的上限，损失函数也可改写为：
[0087][0088]
其中，s(
·
)表示在特定定义域内取得的点的集合，s(i)为在定义域内采样得到的点，为初始点或边界点集。函数的第一部分为所有网格点在微分方程上的损失，第二部分表示该近似解对初边值条件的近似程度。
[0089]
从上式可以看到损失函数中还包含神经网络对输入的微分形式这些值可以通过自动微分(auto differential)技术求得，这在一些机器学习代码库中很容易实现，比如tensorflow、py
′
torch.最后一步，通过最小化损失函数来搜索合适的θ的过程称为”训练”。考虑到损失函数是关于参数向量θ的高度非线性且非凸的函数，我们通常通过基于梯度的优化器(例如梯度下降，adam和l-bfgs)来最小化损失函数。
[0090]
通过上述对损失函数的优化，使得计算更加方便快捷。
[0091]
在一实施例中，所述通过带权重衰减的adam优化算法优化所述损失函数，返回步骤s105直至收敛，包括：
[0092]
计算损失函数的梯度
[0093]
采用以下公式更新参数向量θ：
[0094][0095]
返回步骤s105直至收敛。
[0096]
以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到各种等效的修改或替换，这些修改或替换都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应以权利
要求的保护范围为准。