一种非线性不变子的快速计算方法与流程

1.本发明涉及密码领域，特别涉及一种非线性不变子的快速计算方法。


背景技术：

2.对称密码的设计技术和分析技术是对称密码领域的两大分支，它们相辅相成，共同促进。一个安全的对称密码算法往往需要经过算法设计、分析、改进优化的反复迭代，最终能够抵抗所有的已知攻击。非线性不变分析是在2016年被提出的一种新型攻击方法，它通过计算s盒代数次数为2的非线性不变子来构造关于明密文的区分器，实现成功概率为1的区分攻击。由于实施非线性不变分析需要保证弱密钥的存在性，这要求算法密钥编排算法简单和轮常数设置稀疏，因此非线性不变分析主要用于分析轻量级分组密码算法。目前，非线性不变分析已成功分析midori算法、scream算法和iscream算法，它们的攻击前提都是先计算出s盒代数次数为2的非线性不变子。
3.将s盒看作n比特输入n比特输出的布尔函数，那么对于任意的输入x＝(x
n-1
,x
n-2
,
…
,x0)，有输出y＝(y
n-1
,y
n-2
,
…
,y0)，满足y＝s(x)。若存在一个非线性布尔函数g，使得对于任意的输入x，式g(s(x))＝g(x) c恒成立，其中c∈f2，f2表示由0和1构成的二元域集合，则将布尔函数g称为s盒的非线性不变子。
4.本质上非线性不变子是一个n元布尔函数，而任意一个n元布尔函数f都可以写成代数正规型的形式，即
[0005][0006]
其中au∈f2称为单项式xu的系数，单项式xu的具体形式为：当u＝0时，xu＝1；否则，将正整数u转化为n比特的二进制数u
n-1un-2
...u0，u0称为最低有效位，u
n-1
称为最高有效位，此时提取所有的系数组成2n维向量称之为布尔函数的f的系数向量。f的代数正规型中系数非零单项式的个数称为f的项数，所有系数非零单项式的代数次数的最大值称为布尔函数f的代数次数。非负整数的汉明重量定义为其二进制表示中非零比特的个数。
[0007]
计算s盒代数次数为2的非线性不变子是成功实施非线性不变分析的关键。传统的计算方法主要包括三个步骤：计算分量函数的布尔表达式、计算系数矩阵、对矩阵高斯消元。由于无法指定代数次数，传统的计算方法在计算系数矩阵时，需要对所有的非负整数k计算xk yk，计算次数共计2n，并且随着k的汉明重量的增加，yk的计算复杂度急剧增加。矩阵高斯消元时，矩阵的大小为2n行2
n 1
列。
[0008]
传统的计算方法能够将s盒所有的非线性不变子都计算出来，然后筛选出代数次数为2的非线性不变子。但非线性不变子的数量往往是指数级的，比如iscream算法8比特s盒的非线性不变子的数量达到2
136-1，而代数次数为2的非线性不变子往往只占其中一小部分。这使得计算出来的非线性不变子大多数都是无效的，造成了计算资源和存储资源的严
重浪费，计算效率十分低下。


技术实现要素：

[0009]
针对现有技术中存在的问题，提供了一种非线性不变子的快速计算方法，能够快速计算出s盒代数次数为2的非线性不变子，避免了计算资源和存储资源的浪费，计算效率得到了较大的提高。
[0010]
本发明采用的技术方案如下：一种非线性不变子的快速计算方法，基于计算机程序执行计算过程，包括：
[0011]
步骤1、设定有效非线性不变子的代数次数；
[0012]
步骤2、对待计算的n比特输入、n比特输出的布尔函数f，满足(y
n-1
,y
n-2
,...,y0)＝f(x
n-1
,x
n-2
,...,x0)，根据布尔函数f的真值表计算各分量函数的布尔表达式；
[0013]
步骤3、获取所有汉明重量不超过代数次数的正整数，根据正整数获取系数矩阵mf；
[0014]
步骤4、引入辅助矩阵ef对系数矩阵mf扩展得到扩展矩阵[mf,ef]，对扩展矩阵[mf,ef]进行高斯消元，得到矩阵[m1,m2]；
[0015]
步骤5、遍历矩阵m1中的行向量，若取值为[0,0,
…
,0]或[1,0,
…
,0]，则将m2中相同位置的行向量看作系数向量，转化为布尔表达式；
[0016]
步骤6、计算得到的布尔表达式的所有非零线性组合，若非零线性组合的代数次数为设定的代数次数，则作为非线性不变子输出。
[0017]
进一步的，所述步骤3中，所述正整数为ki，满足其中，d为设定的代数次数。
[0018]
进一步的，所述获取系数矩阵mf的步骤为：
[0019]
步骤3.1、根据正整数ki计算
[0020]
步骤3.2、根据步骤3.1的计算结果提取系数向量由系数向量构建系数矩阵
[0021]
进一步的，所述步骤3.1的具体过程为：
[0022]
步骤3.1.1、将ki转化为n比特的二进制数k
i,n-1ki,n-2
...k
i,0
；
[0023]
步骤3.1.2、计算
[0024]
步骤3.1.3、将步骤2得到的各分量函数的布尔表达式分别代入步骤3.1.2的计算公式中，消除所有的变量yj，化简后输出计算结果。
[0025]
进一步的，所述步骤3.2中，系数向量其中的取值要么为0，要么为1，j＝0,1,...,2
n-1；
[0026]
当单项式xj出现在化简后的布尔表达式中时，否则，其中单项式xj具体为：将j转化为n比特的二进制数j
n-1jn-2
…
j0，在j＝0时，xj＝1。
[0027]
进一步的，所述辅助矩阵ef由2n维单位向量构成，具体为：
[0028][0029]
其中，2n维单位向量是指第ki 1个元素取值为1的单位向量，即其中具体取值为：当j＝ki时，否则，
[0030]
进一步的，所述步骤s4中m1和m2为行2n列的矩阵。
[0031]
与现有技术相比，采用上述技术方案的有益效果为：本发明提供的方法，极大程度上节省了计算资源和存储资源，有效降低了计算和筛选的复杂度，计算效率显著提高。
附图说明
[0032]
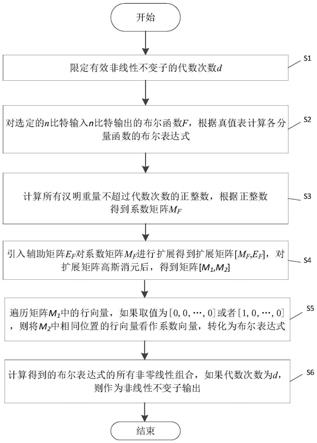
图1为本发明提出的非线性不变子的快速计算流程图。
具体实施方式
[0033]
下面结合附图对本发明做进一步描述。
[0034]
如图1所示，本实施例提供了一种非线性不变子的快速计算方法，由计算机执行计算过程，具体包括：
[0035]
s1、限定有效非线性不变子的代数次数d；
[0036]
s2、对选定的n比特输入n比特输出的布尔函数f，满足(y
n-1
,y
n-2
,...,y0)＝f(x
n-1
,x
n-2
,...,x0)，根据真值表计算各分量函数的布尔表达式；
[0037]
s3、获取所有汉明重量不超过d的正整数ki，满足分别计算提取系数向量得到系数矩阵mf；一个正整数的汉明重量是指其对应的二进制数中非零比特的个数。
[0038]
s4、引入辅助矩阵ef对系数矩阵mf扩展得到扩展矩阵[mf,ef]，对扩展矩阵[mf,ef]进行高斯消元，得到矩阵[m1,m2]；其中，m1和m2都是行2n列的矩阵。
[0039]
s5、遍历矩阵m1中的行向量，如果取值为[0,0,
…
,0]或者[1,0,
…
,0]，则将m2中相
同位置的行向量看作系数向量，转化为布尔表达式；
[0040]
s6、计算这些布尔表达式的所有非零线性组合，如果代数次数为d，则作为非线性不变子输出。
[0041]
具体的所述步骤s3中的计算过程为：
[0042]
s31、将ki转化为n比特的二进制数k
i,n-1ki,n-2
...k
i,0
；
[0043]
s32、计算k
i,j
的取值用于判定某一个输入变量或者输出变量是否出现在乘积项中。
[0044]
s33、将s2得到的各分量函数的布尔表达式分别代入s32的计算公式中，化简后输出。
[0045]
具体的，步骤s2计算得到各分量的布尔表达式，形式如下：y0＝f0(x0,x1,...,x
n-1
),y1＝f1(x0,x1,...,x
n-1
),...,y
n-1
＝f
n-1
(x0,x1,...,x
n-1
),将这些n入1出布尔函数表达式代入步骤s32公式yj中，从而消除输出变量y0,y1,...,y
n-1
，最终化简得到关于输入变量x0,x1,...,x
n-1
的布尔函数。
[0046]
在得到简化后的布尔表达式后，即可计算系数向量；所述系数向量其中的取值要么为0，要么为1，j＝0,1,...,2
n-1；
[0047]
系数向量的取值方法为：当单项式xj出现在化简后的布尔表达式中时，否则，
[0048]
其中，所述单项式xj是指：将j转化为n比特的二进制数j
n-1jn-2
...j0，特别地，当j＝0时，xj＝1。
[0049]
最终，对得到的系数向量进行排列即可得系数矩阵mf具体为
[0050][0051]
在本实施例中，所述s4中引入的辅助矩阵ef由2n维单位向量构成，具体为
[0052][0053]
其中，2n维单位向量是指第ki 1个元素取值为1的单位向量，即其中的具体取值为：当j＝ki时，否则，
[0054]
在本实施例中，还提供了一种代数次数为2的非线性不变子的快速计算方法进行验证。
[0055]
限定有效非线性不变子的代数次数d＝2，以轻量级密码算法midori64算法的4比特s盒为例，s∈f，使用快速计算方法，计算其代数次数为2的非线性不变子。s盒的真值表如表1所示。
[0056]
表1 s盒真值表
[0057][0058]
计算过程如下：
[0059]
s1、对选定的4比特输入4比特输出s盒，满足(y3,y2,y1,y0)＝s(x3,x2,x1,x0)，根据真值表计算各分量函数的布尔表达式，结果如下：
[0060]
y0＝x1 x0x2 x0x1x2 x0x3 x0x1x3 x1x2x3；
[0061]
y1＝x0 x2 x0x2 x0x3 x2x3；
[0062]
y2＝1 x0 x0x1x2 x3 x0x3 x0x1x3 x1x2x3；
[0063]
y3＝1 x0x1 x1x3 x0x1x3 x2x3 x1x2x3；
[0064]
s2、对所有汉明重量不超过2的正整数ki，i＝0,1,...,9；在本实施例中，k0＝1，k1＝2，k2＝3，k3＝4，k4＝5，k5＝6，k6＝8，k7＝9，k8＝10，k9＝12，具体的说明如下：
[0065]
4比特的s盒，根据正整数ki的取值范围0《ki《16，汉明重量不超过2的有1、2、3、4、5、6、8、9、10、12，共10个正整数。其中1、2、4、8对应的二进制数非零比特的个数为1，它们的汉明重量为1，3、5、6、9、10、12对应的二进制数非零比特个数为2，它们的汉明重量为2。因此，根据取值规则k0《k1《
…
《k9，可知k0＝1，k1＝2，k2＝3，k3＝4，k4＝5，k5＝6，k6＝8，k7＝9，k8＝10，k9＝12。
[0066]
分别计算提取系数向量得到系数矩阵mf，结果如下：
[0067][0068]
s3、引入辅助矩阵ef得到扩展矩阵[mf,ef]，其中
[0069][0070]
对扩展矩阵[mf,ef]进行高斯消元，得到矩阵[m1,m2]，结果如下：
[0071][0072]
s4、遍历矩阵m1中的行向量，取值为[0,0,
…
,0]的行向量共4个，将m2中相同位置的行向量看作系数向量，转化为布尔表达式，结果如下：
[0073]
x0 x3 x0x3 x2x3；
[0074]
x2 x0x1 x1x2 x2x3；
[0075]
x0 x1 x2 x2x3；
[0076]
x0x2 x0x3；
[0077]
s5、计算这些布尔表达式的所有非零线性组合，共15种非零线性组合，代数次数都为2，由此，即可得到s盒代数次数为2的非线性不变子共计15个，具体为：
[0078]
g0＝x0 x3 x0x3 x2x3；
[0079]
g1＝x2 x0x1 x1x2 x2x3；
[0080]
g2＝x0 x2 x3 x0x3 x0x1 x1x2；
[0081]
g3＝x0 x1 x2 x2x3；
[0082]
g4＝x1 x2 x3 x0x3；
[0083]
g5＝x0 x1 x0x1 x1x2；
[0084]
g6＝x1 x3 x0x3 x0x1 x1x2 x2x3；
[0085]
g7＝x0x2 x0x3；
[0086]
g8＝x0 x3 x2x3 x0x2；
[0087]
g9＝x2 x0x1 x1x2 x2x3 x0x2 x0x3；
[0088]g10
＝x0 x2 x3 x0x1 x1x2 x0x2；
[0089]g11
＝x0 x1 x2 x2x3 x0x2 x0x3；
[0090]g12
＝x1 x2 x3 x0x2；
[0091]g13
＝x0 x1 x0x1 x1x2 x0x2 x0x3；
[0092]g14
＝x1 x3 x0x1 x1x2 x2x3 x0x2。
[0093]
在本实施例中，本发明提出的方法能够快速计算s盒代数次数为2的非线性不变子；通过限定有效非线性不变子的代数次数d＝2，计算时只需考虑汉明重量为1和汉明重量为2的正整数k，将xk yk的计算次数由2n次大幅度减少至次，同时避免了高汉明重量k对应的yk的计算，大大降低了系数矩阵mf的计算复杂度，扩展矩阵的维数也由2n行2
n 1
列降低至行2
n 1
列，降低了矩阵高斯消元的复杂度。
[0094]
本发明并不局限于前述的具体实施方式。本发明扩展到任何在本说明书中披露的新特征或任何新的组合，以及披露的任一新的方法或过程的步骤或任何新的组合。如果本领域技术人员，在不脱离本发明的精神所做的非实质性改变或改进，都应该属于本发明权利要求保护的范围。
[0095]
本说明书中公开的所有特征，或公开的所有方法或过程中的步骤，除了互相排斥的特征和/或步骤以外，均可以以任何方式组合。
[0096]
本说明书中公开的任一特征，除非特别叙述，均可被其他等效或具有类似目的的替代特征加以替换。即，除非特别叙述，每个特征只是一系列等效或类似特征中的一个例子而已。