一种基于穿越率的时变可靠度快速分析方法与流程

1.本发明涉及工程结构时变可靠度分析技术领域，具体涉及一种基于穿越率的时变可靠度快速分析方法。


背景技术：

2.结构可靠性分析旨在评估工程结构或结构体系在服役期内完成预期功能的概率。由于结构的材料特性(如混凝土弹性模量、钢筋锈蚀程度等)以及外部载荷(如风荷载、列车荷载等)均具有明显的时变性和随机性，需要对实际工程结构开展时变可靠度分析。因为增加了时间维度，所以时变可靠度分析较经典时不变可靠度分析具有更加复杂耗时的特点，如何高效准确的开展时变可靠度分析是当前面临的重大科学问题。
3.结构时变可靠度分析的首要任务是计算[0，t]服役期内结构的累积失效概率p
f,c
(0,t)。理论上讲，结构在[0，t]时间段内的失效定义为其极限状态函数g(x,y(t),t)在[0,t]内出现至少一次负值，即失效事件e
f
＝{t∈[0,t]:g(x,y(t),t)≤0}。其中，x＝{x1,...，x
i
，...,x
n
}表示n维随机变量向量，y(t)＝{y1(t),...，y
i
(t)，...，y
m
(t)}表示m维随机过程向量，t表示时刻。因此，p
f，c
(0，t)的理论定义为p
f，c
(0，t)＝prob[{t∈[0,t]:g(x，y(t),t)≤0}]。基于p
f,c
(0,t)理论定义的基本时变可靠度分析方法为蒙特卡洛方法(monte carlo simulation，mcs)。该方法通过生成大量x和y(t)的随机样本，对g(x，y(t)，t)的所有可能取值进行模拟，从而得到p
f，c
(0，t)的估计值。虽然mcs具有较为坚实的理论基础，但该方法需要进行大量数值模拟，计算效率极低，难以用于工程实践。因此mcs主要作为准确性判定依据用于科学研究。
[0004]
因为基于p
f，c
(0,t)理论公式的时变可靠度分析难以实现，所以发展了一系列基于穿越事件的时变可靠度分析方法。在基于穿越事件的时变可靠度分析方法中，结构在[0,t]时间段内的失效e
f
等价表示为结构在初始时刻失效或在(0，t]时段内发生至少一次穿越事件。其中，结构在t时刻的穿越事件定义为g(x，y(t),t)在该时刻从正值变为负值。据此，p
f,c
(0,t)可以表示为：
[0005]
p
f,c
(0,t)＝prob[{g(x,y(0),0)≤0}∪{n

(0,t)＞0}]
[0006]
式中：n

(0,t)表示(0,t]时间段内发生穿越事件的个数。
[0007]
实际工程中，结构往往具有较高的可靠度，穿越事件鲜少发生。因此，对于具有高可靠水平的结构，可以认为不同时刻的穿越事件之间相互独立。采用泊松过程模拟相互独立的穿越事件，p
f,c
(0,t)可以表示为：
[0008][0009]
式中：p
f,i
(0)为初始时刻的时不变失效概率，ν

(t)表示t时刻的瞬时穿越率。
[0010]
准确求解穿越率ν

(t)是基于穿越事件累积失效概率p
f,c
(0,t)的核心问题之一，目前较为常用的方法主要包括phi2 时变可靠度分析方法及mphi2时变可靠度分析方法。前者面临无法适用于求导困难极限状态函数的问题，后者无法适用于高维极限状态函数。同时，两者均需要大量计算不同时刻处的ν

(t)，计算效率较低。


技术实现要素：

[0011]
本发明针对现有技术存在的问题提供一种不受极限状态函数形式的限制，计算效率高的基于穿越率的时变可靠度快速分析方法。
[0012]
本发明采用的技术方案是：
[0013]
一种基于穿越率的时变可靠度快速分析方法，包括以下步骤：
[0014]
步骤1：根据结构的极限状态建立极限状态函数；
[0015]
步骤2：对步骤1建立的极限状态函数在均值处求导，判断求导计算时间t
d
是否超过1分钟；若t
d
≥1分钟，采用高阶矩法计算初始时刻的失效概率p
f,i
(0)；若t
d
＜1分钟，采用form时不变可靠度分析方法计算初始时刻的失效概率p
f,i
(0)；
[0016]
步骤3：确定用于计算累积失效概率的积分点向量τ；
[0017]
步骤4：定义时变可靠度分析循环中的初始值，序列号k＝1，累积失效概率p
f,c
(0,t)＝p
f,i
(0)；
[0018]
步骤5：对τ
k
时刻的极限状态函数在均值处求导，判断求导计算时间t
d
是否超过1分钟；t
d
≥1分钟，采用mphi2方法计算该时刻的穿越率；若t
d
＜1分钟，采用phi2 方法计算该时刻的穿越率；
[0019]
步骤6：根据穿越率更新累积失效概率，更新序列号k＝k 1；
[0020]
步骤7：判断序列号k是否小于设定次数n，若k＜n，重复转入步骤5，若k＝n则输出累积失效概率，完成结构的可靠度分析。
[0021]
进一步的，所述步骤2中采用高阶矩法计算初始时刻的失效概率过程如下：
[0022]
计算极限状态函数的前四阶矩，采用四阶矩可靠指标模型求解初始时刻瞬时可靠指标，计算初始时刻失效概率。
[0023]
进一步的，所述步骤5中采用mphi2计算该时刻的穿越率过程如下：
[0024]
τ
k
时刻的极限状态函数为g(x，y(τ
k
)，τ
k
)；x＝{x1，...，x
i
，...，x
n
}表示n维随机变量向量，y(t)＝{y1(t),...，y
i
(t),...，y
m
(t)}表示m维随机过程向量，t表示时刻；
[0025]
s11：确定分解y(τ
k
)的时间增量δt
m
；
[0026]
s12：固定时间变量，将随机过程表示为两组相关随机向量y(τ
k
)和y(τ
k
δt
m
)；
[0027]
s13：采用cholesky分解，将y(τ
k
)和y(τ
k
δt
m
)表示为两组相互独立的随机变量ξ(τ
k
)和ξ(τ
k
δt
m
)，建立对应的极限状态函数g(x,ξ(τ
k
),τ
k
)和g(x,ξ(τ
k
δt
m
),τ
k
δt
m
)；
[0028]
s14：采用基于二维减维的点估计方法估计极限状态函数g(x,ξ(τ
k
),τ
k
)和g(x,ξ(τ
k
δt
m
),τ
k
δt
m
)的前四阶中心矩及g
m
＝g(x,ξ(τ
k
),τ
k
)g(x,ξ(τ
k
δt
m
),τ
k
δt
m
)的均值；
[0029]
s15：基于四阶矩可靠度模型计算τ
k
时刻和τ
k
δt
m
时刻对应的瞬时高阶矩可靠指标β
m
(τ
k
)和β
m
(τ
k
δτ
m
)；基于相关系数四阶矩转换模型计算τ
k
时刻和τ
k
δt
m
时刻极限状态函数在正态空间内的相关系数
[0030]
s16：计算穿越率
[0031]
式中：是基于mphi2方法定义的τ
k
时刻穿越率，φ2(
…
，
…
；
…
)表示二维正态分布的累积分布函数。
[0032]
进一步的，所述步骤5中采用phi2 方法计算该时刻的穿越率过程如下：
[0033]
τ
k
时刻的极限状态函数为g(x,y(τ
k
),τ
k
)；x＝{x1,...,x
i
,...,x
n
}表示n维随机变量向量，y(t)＝{y1(t),...,y
i
(t),...,y
m
(t)}表示m维随机过程向量，t表示时刻；
[0034]
s21：确定分解y(τ
k
)的时间增量δτ

；
[0035]
s22：固定时间变量，将随机过程表示为两组相关随机向量y(τ
k
)和y(τ
k
δτ

)；
[0036]
s23：采用cholesky分解，将y(τ
k
)和y(τ
k
δτ

)表示为两组相互独立的随机变量ξ(τ
k
)和ξ(τ
k
δt

)，建立对应的极限状态函数g(x,ξ(τ
k
),τ
k
)和g(x,ξ(τ
k
δt
m
),τ
k
δt

)；
[0037]
s24：采用form时不变可靠度分析方法计算τ
k
和τ
k
δτ

时刻的瞬时可靠指标β(τ
k
)和β(τ
k
δτ

)，获得相应的验算点u
*
(τ
k
)和u
*
(τ
k
δτ

)；
[0038]
s25：根据步骤s24得到的对应时刻的验算点计算单位法向向量和
[0039]
s26：计算穿越率
[0040]
式中：是基于phi2 方法定义的τ
k
时刻穿越率，||
·
||表示矩阵的秩，表示标准正态分布的概率密度函数；表示一种函数运算，φ[y]表示标准正态分布累积分布函数。
[0041]
进一步的，所述时间增量δt
m
的取值使y(τ
k
)及y(τ
k
)间相关系数在[0.99,0.995]范围内。
[0042]
进一步的，所述时间增量δτ

取y(τ
k
)自相关长度的1％。
[0043]
本发明的有益效果是：
[0044]
(1)本发明可以高效开展针对任意长度时间段的时变可靠度分析，不受极限状态函数形式的限制；
[0045]
(2)本发明方法计算效率与现有方法相比显著提高，计算时间不随时间段的长度增长而提高；可以高效用于高维极限状态函数的时变可靠度分析，且计算效率不受时间段长短的影响；
[0046]
(3)本发明方法可以高效用于极限状态函数的时变可靠度分析，且计算效率不受时间段长短的影响。
附图说明
[0047]
图1为本发明方法流程示意图。
[0048]
图2为现有phi2 方法流程示意图。
[0049]
图3为现有mphi2方法流程示意图。
[0050]
图4为实施例1中的锈蚀简支钢梁模型示意图。
[0051]
图5为实施例1中不同时变可靠度分析方法结果对比示意图，a为累积失效概率，b为计算时间。
[0052]
图6为实施例2中不同时变可靠度分析方法结果对比示意图，a为累积失效概率，b
为计算时间。
具体实施方式
[0053]
下面结合附图和具体实施例对本发明做进一步说明。
[0054]
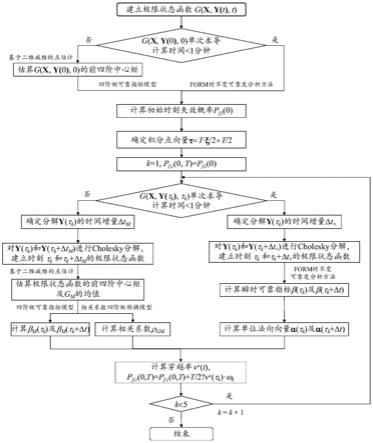
如图1所示，一种基于穿越率的时变可靠度快速分析方法，包括以下步骤：
[0055]
步骤1：根据结构的极限状态建立极限状态函数g(x,y(t),t)；
[0056]
步骤2：对步骤1建立的极限状态函数在均值处求导，判断求导计算时间t
d
是否超过1分钟；若t
d
≥1分钟，采用高阶矩法计算初始时刻的失效概率p
f,i
(0)；采用高阶矩法计算初始时刻的失效概率过程如下：
[0057]
计算极限状态函数的前四阶矩，采用四阶矩可靠指标模型求解初始时刻瞬时可靠指标β(0)，计算初始时刻失效概率p
f，i
＝φ[β(0)]。
[0058]
若t
d
＜1分钟，采用form时不变可靠度分析方法计算初始时刻的失效概率p
f，i
(0)；
[0059]
步骤3：确定用于计算累积失效概率的积分点向量τ＝tξ/2 t/2；其中ξ为高斯
‑
勒让德积分的原始积分向量。
[0060]
令t＝tξ/2 t/2，累积失效概率p
f,c
(0,t)理论计算公式可以表示为：
[0061][0062]
上式中穿越率积分范围为(
‑
1,1]，因此可以使用高斯
‑
勒让德积分原理将该积分表示为5个特定时刻处穿越率加权求和的形式。此时，p
f,c
(0,t)可由下式计算：
[0063][0064]
式中τ
k
＝tξ
k
/2 t/2为第k个积分点。ξ
k
和ω
k
分别是高斯
‑
勒让德积分的第k个原始积分点和权重系数，如表1所示。
[0065]
表1.高斯勒让德积分的原始积分点及权重系数
[0066][0067]
步骤4：定义时变可靠度分析循环中的初始值，序列号k＝1，累积失效概率p
f，c
(0，t)＝p
f，i
(0)；
[0068]
步骤5：对τ
k
时刻的极限状态函数在均值处求导，判断求导计算时间t
d
是否超过1分钟；t
d
≥1分钟，采用mphi2方法计算该时刻的穿越率；
[0069]
采用mphi2计算该时刻的穿越率过程如下：
[0070]
τ
k
时刻的极限状态函数为g(x，y(τ
k
)，τ
k
)；x＝{x1，...，x
i
，...，x
n
}表示n维随机变量向量，y(t)＝{y1(t)，...，y
i
(t),...，y
m
(t)}表示m维随机过程向量，t表示时刻；
[0071]
s11：确定分解y(τ
k
)的时间增量δt
m
；δt
m
的取值使y(τ
k
)及y(τ
k
)间相关系数在[0.99,0.995]范围内；
[0072]
s12：固定时间变量，将随机过程表示为两组相关随机向量y(τ
k
)和y(τ
k
δt
m
)；
[0073]
s13：采用cholesky分解，将y(τ
k
)和y(τ
k
δt
m
)表示为两组相互独立的随机变量ξ
(τ
k
)和ξ(τ
k
δt
m
)，建立对应的极限状态函数g(x,ξ(τ
k
),τ
k
)和g(x,ξ(τ
k
δt
m
),τ
k
δt
m
)；
[0074]
s14：采用基于二维减维的点估计方法估计极限状态函数g(x,ξ(τ
k
),τ
k
)和g(x,ξ(τ
k
δt
m
),τ
k
δt
m
)的前四阶中心矩及g
m
＝g(x，ξ(τ
k
)，τ
k
)g(x,ξ(τ
k
δt
m
)，τ
k
δt
m
)的均值；
[0075]
s15：基于四阶矩可靠度模型计算τ
k
时刻和τ
k
δt
m
时刻对应的瞬时高阶矩可靠指标β
m
(τ
k
)和β
m
(τ
k
δτ
m
)；基于相关系数四阶矩转换模型计算τ
k
时刻和τ
k
δt
m
时刻极限状态函数在正态空间内的相关系数
[0076]
s16：计算穿越率
[0077]
式中：是基于mphi2方法定义的τ
k
时刻穿越率，φ2(
…
，
…
；
…
)表示二维正态分布的累积分布函数。
[0078]
若t
d
＜1分钟，采用phi2 方法计算该时刻的穿越率；
[0079]
采用phi2 方法计算该时刻的穿越率过程如下：
[0080]
τ
k
时刻的极限状态函数为g(x，y(τ
k
)，τ
k
)；x＝{x1,...,x
i
,...,x
n
}表示n维随机变量向量，y(t)＝{y1(t)，...，y
i
(t)，...，y
m
(t)}表示m维随机过程向量，t表示时刻；
[0081]
s21：确定分解y(τ
k
)的时间增量δτ

；δτ

的取值应取为y(τ
k
)自相关长度的1％；
[0082]
s22：固定时间变量，将随机过程表示为两组相关随机向量y(τ
k
)和y(τ
k
δτ

)；
[0083]
s23：采用cholesky分解，将y(τ
k
)和y(τ
k
δτ

)表示为两组相互独立的随机变量ξ(τ
k
)和ξ(τ
k
δt

)，建立对应的极限状态函数g(x,ξ(τ
k
)，τ
k
)和g(x,ξ(τ
k
δt
m
),τ
k
δt

)；
[0084]
s24：采用form时不变可靠度分析方法计算τ
k
和τ
k
δτ

时刻的瞬时可靠指标β(τ
k
)和β(τ
k
δτ

)，获得相应的验算点u
*
(τ
k
)和u
*
(τ
k
δτ

)；
[0085]
s25：根据步骤s24得到的对应时刻的验算点计算单位法向向量和
[0086]
s26：计算穿越率
[0087]
式中：是基于phi2 方法定义的τ
k
时刻穿越率，||
·
||表示矩阵的秩，表示标准正态分布的概率密度函数；表示一种函数运算，φ[y]表示标准正态分布累积分布函数。
[0088]
步骤6：根据穿越率更新累积失效概率更新序列号k＝k 1；
[0089]
步骤7：判断序列号k是否小于设定次数n，若k＜n，重复转入步骤5，若k＝n则输出累积失效概率，完成结构的可靠度分析。
[0090]
基于式2的时变可靠度分析方法仅需5次穿越率，与现有方法100次以上的计算量相比，可以大大减少计算时间，提高计算效率。计算穿越率是本发明方法的核心，现有方法无法同时适用于高维极限状态函数及求导困难极限状态函数的问题，本发明方法中以极限
状态函数在均值处的单次求导时间是否大于1分钟为判别标准，大于一分钟采用mphi2方法计算穿越率，小于1分钟采用phi2 计算穿越率。
[0091]
本发明方法可以高效开展针对任意长度时间段的时变可靠度分析，不受极限状态函数形式的限制。
[0092]
实施例1
[0093]
以如图4所示的锈蚀简支钢梁模型为例进行时变可靠度分析，考虑的极限状态由跨中截面的极限抗弯能力决定，相应的极限状态函数由下式给出：
[0094][0095]
式中：f
y
为钢材屈服强度，b0为梁截面长度，h0为梁截面宽度，l为钢梁跨度，ρ
st
为钢材密度，f
i
(t)(i＝1，,10)为集中荷载，k＝0.03mm/年为钢材锈蚀速率。集中荷载f
i
(t)(i＝1，,10)为相互独立的高斯过程，其余变量为相互独立的随机变量。随机过程及随机变量统计信息如表2所示。由于极限状态函数含有15个随机变量，本示例为高维问题。
[0096]
表2.实施例1中的随机变量和随机过程统计特征
[0097][0098]
分别采用phi2 方法、mphi2方法、蒙特卡洛方法(monte carlo simulation，mcs)及本发明方法分析本实施例的时变可靠度，以mcs方法得到的结果作为验证不同方法准确性的标准。其中，phi2 方法流程示意图如图2所示，mphi2方法流程示意图如图3所示，mcs方法为现有计算方法，具体的计算方法在此不再赘述。
[0099]
phi2 与mphi2以dt＝0.1年为时间间隔均匀划分时间段，而mcs以dt＝0.05年为时
间间隔均匀划分时间段且每个时刻采用107个样本进行分析。为充分说明本发明方法的有益效果，预测时间段[0,t]的长度变化范围为1年到30年，即t∈[1年，30年]。不同方法得到的累积失效概率及相应的计算时长如图5a和图5b所示，部分代表值如表3所示。
[0100]
表3.实施例1中的随机变量和随机过程统计特征
[0101][0102][0103]
从图5和表3可以看出，本发明方法计算效率与现有方法相比显著提高，且计算时间不随时间段的长度增长而提高。如t＝10年时，本发明方法所需计算时间为0.03分钟，而phi2 和mphi2方法分别需要0.56分钟和578.1分钟。t＝30年时，本发明方法所需计算时间仍然为0.03分钟，而phi2 和mphi2方法分别需要1.74分钟和177.2分钟。这说明，本发明方法可以用于高维极限状态函数的时变可靠度分析，并且计算效率不受时间段长短的影响。
[0104]
实施例2
[0105]
以桥上高速铁路crts ii型轨道板的纵横向开裂失效模式为例进行时变可靠度分析。crts ii型轨道板为crts ii型板式无砟轨道的重要结构层。考虑到该轨道板纵向在预裂缝处的裂缝宽度不可以超过极限且其横向不允许开裂，因此其极限状态函数的定义为：
[0106][0107][0108][0109]
δ
tk
＝λ
s
e
s
a
ts
δt,δt
ttk
＝λ
s
e
s
a
ts
t
g
h/2,δ
ck
＝λ
s
e
s
a
ts
δt
ck
ꢀꢀ
(9)
[0110][0111]
式中：m
cr
＝52.942kn.m为初始横向抗裂弯矩，可以基于试验确定；κ
m
＝0.003/年为m
cr
的退化速率，m
fh
(t)为竖向列车荷载作用下的横向时变弯矩，可以由有限元分析模型计算获得。竖向列车荷载使用3p
j
(t)表示，p
j
(t)为时变静轮载，m
l
(t)为横向列车荷载造成的时变横向弯矩，m
th
为温度梯度t
g
引起的横向弯矩，w
max,cr
＝0.4mm为轨道板纵向裂缝允许极限，w
max
为轨道板纵向裂缝宽度。
[0112]
a
ts
＝10
‑5/℃为线膨胀系数，e
c
＝35.5gpa为弹性模量，ν＝0.2为泊松比，h＝0.2m为
轨道板厚度，h
a
＝0.15m为有效厚度，α
cr
＝2.4为荷载调整系数，d
eq
＝8mm为纵向钢筋等效直径，a
sl
＝804mm2受拉区纵向钢筋截面积，a
g
＝0.51m2和a
d
＝0.59m2分别是轨道板和底座板的截面积，c
s
＝0.05m为底座板混凝土保护层厚度，δ
tk
,δ
ttk
,和δ
ck
分别是由轴向温度δt、t
g
及混凝土收缩徐变等效温降δt
ck
引起的钢筋应力；f
b
为纵向列车荷载引起的钢筋拉力；e
s
＝200gpa为钢筋弹性模量；λ
s
＝1/2为e
s
折减系数；a
ts
＝1.2
×
10
‑5/℃为钢筋线膨胀系数；n
cj
＝20为单个轨道板内的扣件个数；f
cj
为扣件阻力；f
c
′
＝1.96mpa及f
′
d
＝1.43mpa分别是轨道板和底座板内混凝土抗拉强度。
[0113]
采用高斯过程模拟p
j
(t)，同时将δt，t
g
，δt
ck
，和f
cj
看作随机变量。上述随机参数的统计特征如表4所示。
[0114]
表4.实施例2中的随机变量和随机过程统计特征
[0115][0116]
由于本实施例采用有限元分析，g(x，y(t)，t)的求导较为耗时(单次计算时间为10min)，所以本算例属于极限状态函数求导困难问题。此时，phi2 方法无法使用。
[0117]
为了进行对比，分别采用mphi2方法和蒙特卡洛方法(monte carlo simulation，mcs)及本发明方法分析本实施例的时变可靠度，以mcs方法得到的结果作为验证不同方法准确性的标准。其中，mphi2以d
t
＝0.1年为时间间隔均匀划分时间段，而mcs以d
t
＝0.05年为时间间隔均匀划分时间段且每个时刻采用105个样本进行分析。
[0118]
为了说明本发明方法的有益效果，预测时间段[0，t]的长度变化范围为1年到20年，即t∈[1年，20年]。不同方法得到的累积失效概率及相应的计算时长如图6a和图6b所示。本发明方法的计算结果与mcs得到的准确值完全一致，对所有时间段，本发明方法计算时长约为3.3分钟。而mphi2方法的计算时长随时间段长度增长而提高，当t＝30年时，mphi2方法的计算时长将达到2012分钟(约33.53小时)。从上述结果可以看出，本发明方法可以显著提高时变可靠度分析的效率，且计算时间不随时间段的长度增长而提高。这说明，本发明方法可以高效用于极限状态函数求导困难的时变可靠度分析，且计算效率不受时间段长短的影响。
[0119]
本发明对于任何长度的时间段都仅需计算五次穿越率，避免了常规方法中对穿越率的大量计算，从而可以提高时变可靠度分析效率。并且，本发明同时适用于高维极限状态函数和求导困难的极限状态函数，具有较大的适用范围。