基于二阶线性自抗扰控制的李雅普洛夫稳定性证明方法与流程

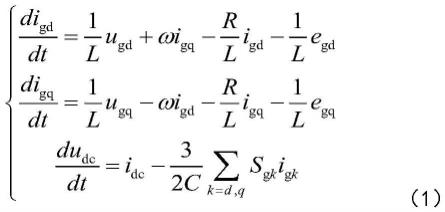
1.本发明涉及一种基于二阶线性自抗扰控制的李雅普洛夫稳定性证明方法。


背景技术：

2.并网逆变系统的稳定性对电网安全运行十分重要，提高并网系统的稳定性仍然是当前研究的关 键技术。目前，大多数方法都是不断的进行控制技术的优化与改进，从技术的角度来提高并网系统 的整体稳定性。那么，在保证并网系统稳定的前提下先对控制技术进行有效地稳定性分析更是至关 重要的。传统控制技术的稳定性分析都是基于频域的方法并结合伯德图来进行研究，虽说在一定程度上大大降低了理论分析的困难程度，但在实际的稳定性体现上却减少了数学分析的严谨性，从而 导致稳定性的证明存在一定的瑕疵。此外，针对目前研究比较火热的人工智能技术、神经元网络技 术、模糊控制技术、滑膜控制技术等等，大多数国内外知名期刊在对该类控制技术的稳定性分析方 面都没有具体的定论。所以，对各种控制技术进行深入的稳定性研究分析，对实际控制器进行研发与设计是重要的前提。


技术实现要素：

3.为解决以上技术上的不足，本发明提供了一种基于二阶线性自抗扰控制的李雅普洛夫稳定性证 明方法，。
4.本发明是通过以下措施实现的：
5.一种基于二阶线性自抗扰控制的李雅普洛夫稳定性证明方法，摆脱了传统控制技术纯频域的 稳定性证明局限，使得控制技术的稳定性证明推导更加严谨可靠有依据。
6.步骤1，建立并网逆变控制系统的二阶数学模型；经简化后如下：
[0007][0008]
式中：e
gd
，e
gq
为电网电压在dq轴上的分量，u
gd
，u
gq
为逆变器输出的电压在dq轴上的 分量，i
gd
，i
gq
为网侧电流在dq轴上的分量，r、l、c为滤波电感内阻、滤波电感以及滤波 电容；u
sabc
、i
sabc
为逆变器侧的三相电压、电流；
[0009]
步骤2，以二阶数学模型为依据，针对并网逆变器设计二阶线性自抗扰控制系统；该二阶线性自 抗扰控制系统包括线性扩张状态观测器及状态误差反馈控制律；
[0010]
将(2)式改写成如下形式:
[0011]
[0012]
式(3)中，b0＝3/(2lc)，x1，x2为母线电压及其微分，x3为leso扩张出来的状态变量，即表示系统的总和扰 动，表示为f，h用来表示f的微分，总和扰动的模型如下：
[0013][0014]
根据(3)式可建立三阶leso：
[0015][0016]
式(5)中，β1、β2、β3为观测器的系数；
[0017]
取系统的控制律为：
[0018][0019]
设pd控制律为：
[0020]
u0＝k
p
(v-z1)-kdz2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0021]
式(7)中，k
p
和kd为比例和微分控制增益；
[0022]
根据极点配置，将(5)式的极点配置在观测器的带宽ω0上，即：
[0023]
λ(s)＝s3 β1s2 β2s β3＝(s ω0)3ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(8)
[0024]
则有：
[0025]
β1＝3ω0，β2＝3ω
02
，β3＝ω
03
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(9)
[0026]
同理可得：
[0027][0028]
并以二阶系统的微分方程为例进行稳定性分析；
[0029]
步骤3，采用李雅普诺夫函数进行验算，判断亚普诺夫渐进稳定性定理是否成立，并给出稳定 性条件。
[0030]
在步骤2中，以二阶系统的微分方程为例进行稳定性分析如下，
[0031][0032]
式(11)中，u和y分别为系统的输入和输出，w为外扰，a0和a1为系统的参数，b为输入控制增 益，b0为其增益估计值。令x1＝y，定义为系统 扰动，令并假定形式的引入扩张状态x1,x2,x3,满足如下公式：
[0033][0034]
式(12)中，x＝[x
1 x
2 x3]
t
；式(12)对应的连续线性系统的三阶leso可以设计为：
[0035][0036]
式(13)中：表示leso观测的未知总扰动；
[0037]
根据上述公式推导，经过参数化，可把特征方程的极点放在(-ω0,ω0)上，即取观测器的增益矩 阵为：
[0038][0039]
设由式(3)、(14)可得leso的估计误差公式为：
[0040][0041]
式(15)中：h(x,ω)表示leso观测的实际值；为进一步对式(15)进行数学分析，现需要对上 式进行化简，假设有则上述公式(15)可简化为：
[0042][0043]
进一步简化可得：
[0044][0045]
式(17)中，令
[0046]
已知leso的双重极点配置在ω0处，则a是hurwitz稳定的，即存在一个正定的赫米特矩阵p 使a满足，则有：
[0047]at
p pa＝-q
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(18)
[0048]
且有：
[0049]
定义李亚普诺夫函数如下：
[0050]
v(ε)＝ε
t
pε
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(19)
[0051]
则有：
[0052]
步骤3中，结合公式(16)和公式(18)可得：
[0053][0054]
由于h(x,ω)在定义域内满足利普希兹连续条件，那么存在一个常数c可满足如下表达式：
[0055][0056]
则有可满足如下公式：
[0057][0058]
由公式(17)和式(21)可知：
[0059][0060]
通过式(24)知，式(23)可进一步简化为：
[0061][0062]
当ω0≥1时，有同时又由于存在如下表达式(26)：
[0063]
||pbc||
2-2||pbc|| 1≥0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(26)
[0064]
所以可进一步推导出式(27)所示的形式：
[0065][0066]
联立式(24)和式(27)可计算出：
[0067][0068]
由式(24)可知，当ω0＞||pbc||2 1时，则存在式(29)：
[0069][0070]
根据李亚普诺夫渐进稳定性的意义有：
[0071][0072]
令并由李亚普诺夫渐进稳定性定理可知：假定h(x,ω)关于x满足全局 lipschitz条件，即存在正数c对任意的满足则存在足够大 的正数ω，使得综合上述推导并结合公式(30)可知，李亚普诺夫渐进 稳定性定理成立，故有线性扩张状态观测器的估计误差在时间趋于无穷时为零，即：
[0073][0074]
由公式(6)和式(7)可知：
[0075][0076]
设e＝v-y1，由式(31)可得：
[0077][0078][0079]
在ladrc技术中，为了避免线性跟踪微分器对噪声的放大作用，一般不进行应用，所以式(34) 可以简化为:
[0080][0081]-k
p
使特征多项式s-k
p
满足劳斯判据，故[-k
p
]是hurwitz稳定的，同时由式(30)可以得 出：所以根据李亚普诺夫渐进稳定性的意义可知ladrc 是渐进稳定的，由此证明出ladrc的稳定性并得出其稳定性条件。
[0082]
本发明的有益效果是：一、本发明摆脱了传统控制技术纯频域的稳定性证明局限；二、使得控 制技术的稳定性证明推导更加严谨可靠有依据；三、与数学深入结合，有利于控制器的研发与设计。
具体实施方式
[0083]
本发明基于二阶线性自抗扰控制的李雅普洛夫稳定性证明方法，对二阶线性自抗扰控制技术 设计出一种严谨的稳定性证明方法。首先，建立一种并网逆变控制系统的二阶数学模型，针对并网 逆变器采用二阶线性自抗扰控制技术。其次，以二阶线性自抗扰控制技术的核心元素—线性扩张状 态观测器(leso)和扰动估计的误差反馈控制律(lsef)为基础。最后，通过引入李亚普诺夫稳定 性理论并结合二阶线性自抗扰控制技术进行稳定性的证明，并给出稳定性条件，从而提出一种基于 二阶线性自抗扰控制技术的李雅普洛夫稳定性证明方法为此，针对并网逆变系统稳定性问题，本文 建立了一种并网逆变控制系统的二阶数学模型，以二阶线性自抗扰控制技术为基础，结合频域方式中的传递函数，通过引用李亚普诺夫稳定性理论，设计推导出一种基于二阶线性自抗扰控制技术的 李雅普洛夫稳定性证明方法，并给出稳定性条件。
[0084]
r、l、c为滤波电感内阻、滤波电感以及滤波电容；u
sabc
、i
sabc
为逆变器侧的三相电压、 电流。
[0085]
逆变器在dq坐标系下的数学模型：
[0086][0087]
式(1)中，e
gd
，e
gq
为电网电压在dq轴上的分量，u
gd
，u
gq
为逆变器输出的电压在dq轴上 的分量，i
gd
，i
gq
为网侧电流在dq轴上的分量。
[0088]
对(1)式简化可得：
[0089][0090]
第2步：传统二阶线性自抗扰控制器的设计：
[0091]
加入扩张状态，可将(2)式改写成如下形式。
[0092][0093]
式(3)中，b0＝3/(2lc)，x1，x2为母线电压及其微分，x3为leso扩张出来的状态变量， 即表示系统的总和扰动，表示为f，h用来表示f的微分，总和扰动的模型如下：
[0094][0095]
根据(3)式可建立三阶leso：
[0096][0097]
式(5)中，β1、β2、β3为观测器的系数。
[0098]
取系统的控制律为：
[0099][0100]
设pd控制律为：
[0101]
u0＝k
p
(v-z1)-kdz2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0102]
式(7)中，k
p
和kd为比例和微分控制增益。
[0103]
根据极点配置，将(5)式的极点配置在观测器的带宽ω0上，即：
[0104]
λ(s)＝s3 β1s2 β2s β3＝(s ω0)3ꢀꢀꢀꢀ
(8)
[0105]
则有：
[0106]
β1＝3ω0，β2＝3ω
02
，β3＝ω
03
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(9)
[0107]
同理可得：
[0108][0109]
第3步：二阶线性自抗扰控制技术的稳定性分析：
[0110]
以二阶系统的微分方程为例进行分析：
[0111][0112]
式(11)中，u和y分别为系统的输入和输出，w为外扰，a0和a1为系统的参数，b为输入控制增 益，b0为其增益估计值。令x1＝y，定义为系统 扰动，令并假定形式的引入扩张状态x1,x2,x3,满足如下公式：
[0113][0114]
式(12)中，x＝[x
1 x
2 x3]
t
。
[0115]
式(12)对应的连续线性系统的三阶leso可以设计为：
[0116][0117]
式(13)中：表示leso观测的未知总扰动。
[0118]
根据上述公式推导，经过参数化，可把特征方程的极点放在(-ω0,ω0)上，即取观测器的增益矩 阵为：
[0119]
l＝[3ω
0 3ω
02 ω
03
]
t
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(14)
[0120]
设由式(3)、(14)可得leso的估计误差公式为：
[0121][0122]
式(15)中：h(x,ω)表示leso观测的实际值。为进一步对式(15)进行数学分析，现需要对上 式进行化简，假设有则上述公式(15)可简化为：
[0123][0124]
进一步简化可得：
[0125][0126]
式(17)中，令
[0127]
已知leso的双重极点配置在ω0处，则a是hurwitz稳定的，即存在一个正定的赫米特矩阵p 使a满足，则有：
[0128]at
p pa＝-q
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(18)
[0129]
且有：
[0130]
为证明控制器的稳定性，特采用李雅普诺夫函数进行证明。定义李亚普诺夫函数如下：
[0131]
v(ε)＝ε
t
pε
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(19)
[0132]
则有：
[0133][0134]
结合公式(16)和公式(18)可得：
[0135][0136]
由于h(x,ω)在定义域内满足利普希兹连续条件，那么存在一个常数c可满足如下表达式：
[0137][0138]
则有可满足如下公式：
[0139][0140]
由公式(17)和式(21)可知：
[0141][0142]
通过式(24)知，式(23)可进一步简化为：
[0143][0144]
当ω0≥1时，有同时又由于存在如下表达式(26)：
[0145]
||pbc||
2-2||pbc|| 1≥0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(26)
[0146]
所以可进一步推导出式(27)所示的形式：
[0147][0148]
联立式(24)和式(27)可计算出：
[0149][0150]
由式(24)可知，当ω0＞||pbc||2 1时，则存在式(29)：
[0151][0152]
根据李亚普诺夫渐进稳定性的意义有：
[0153][0154]
令并由李亚普诺夫渐进稳定性定理可知：假定h(x,ω)关于x满足全局 lipschitz条件，即存在正数c对任意的满足则存在足够大 的正数ω，使得综合上述推导并结合公式(30)可知，李亚普诺夫渐进 稳定性定理成立，故有线性扩张状态观测器的估计误差在时间趋于无穷时为零，即：
[0155][0156]
由公式(6)和式(7)可知：
[0157][0158]
设e＝v-y1，由式(31)可得：
[0159][0160][0161]
在ladrc技术中，为了避免线性跟踪微分器对噪声的放大作用，一般不进行应用，所以式(34) 可以简化为:
[0162][0163]-k
p
使特征多项式s-k
p
满足劳斯判据，故[-k
p
]是hurwitz稳定的，同时由式(30)可以得出：所以根据李亚普诺夫渐进稳定性的意义可知 ladrc是渐进稳定的，由此证明出ladrc的稳定性并得出其稳定性条件。
[0164]
以上所述仅是本专利的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不 脱离本专利技术原理的前提下，还可以做出若干改进和替换，这些改进和替换也应视为本专利的保 护范围。