一种用于非对称双突堤的波浪绕射系数解析方法

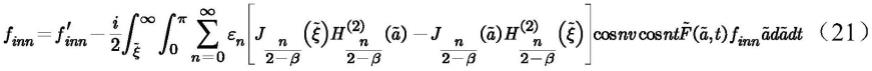
1.本发明涉及海岸工程水动力领域，尤其是涉及一种用于非对称双突堤的波浪绕射系数解析方法。


背景技术：

2.防波堤在海港各类水工建筑物中重要地位，通常建造在开敞海岸、海湾或岛屿的港口，用来形成有掩护的水域，其一旦破坏，不但影响港口的正常使用，而且也可能使得停泊在港域中的船舶发生事故，以及造成港内建筑物的破坏。因此，防波堤的合理规划布置至关重要。考虑港内波浪要素是合理规划布置防波堤的重要前提。目前，计算港内波浪要素时以考虑波浪绕射为主。
3.目前，关于防波堤的波浪绕射现象的研究，多限于单突堤、共线的双突堤和岛式堤。但在实际工程中，防波堤的布置形式可以概化为多种形式，典型如图2所示的非对称平面布置形式。对于这些非对称布置构型的防波堤，研究还很少。


技术实现要素：

4.本发明的目的就是为了克服上述现有技术存在的缺陷而提供了一种用于非对称双突堤的波浪绕射系数解析方法。
5.本发明的目的可以通过以下技术方案来实现：
6.本发明给出了一种用于非对称双突堤的波浪绕射系数解析方法，该方法包括以下步骤：
7.步骤s1、建立笛卡尔坐标系下的非对称式防波堤模型；
8.步骤s2、基于速度势函数及线性化自由面边界条件，得到关于速度势函数中复函数的helmholtz方程；采用schwarz-christoffel保角变换以及格林函数法对helmholtz方程进行边值求解，得到不同非对称式防波堤布置构型的波浪绕射系数模型；
9.步骤s3、采用法对波浪绕射系数模型进行数值求解，得到波浪绕射系数解析值。
10.优选地，所述步骤s1具体为：
11.在笛卡尔坐标系oxyz中布置两个半无限长的防波堤，定义x、y轴位于水平面上，z轴垂直向上，均匀水深hs；其中，第一防波堤置于x轴正半轴，且固定端位于原点o点；第二防波堤以与x轴正方向呈βπ夹角倾斜布置，且固定端位于y轴上半轴的d点；两个防波堤间的口门宽度od为l；
12.波浪以沿与x轴正方向夹角为α的方向入射传播。
13.优选地，所述步骤s2中基于速度势函数及线性化自由面边界条件，得到关于速度势函数中复函数的helmholtz方程，具体为：
14.假设流体不可压且无旋，则存在速度势函数并满足laplace方程，线性化自由面边界条件，得到速度势函数φ(x，y，z，t)的边值问题，数学表达式为：
[0015][0016][0017][0018][0019]
式中，x、y、z分别为笛卡尔坐标系下的坐标，hs为均匀水深，η为自由表面位移，g为重力加速度，t为时间；
[0020]
由式(1)-(2)，得到速度势函数φ(x，y，z，t)的数学表达式为：
[0021]
φ(x，y，z，t)＝a coshk(z hs)f(x，y)e
iσt
ꢀꢀ
(5)
[0022]
式中，k为波数，为波长；σ为角频率，f(x，y)是复函数，a为振幅；
[0023]
将式(5)代入式(1)，得到关于复函数f(x，y)的helmholtz方程：
[0024][0025]
将式(5)代入式(3)-(4)得到频散关系式：
[0026]
σ2＝gktanh(khs)
ꢀꢀ
(7)
[0027]
绕流边界条件为：
[0028][0029]
式中，为法向量，γ为在水面处的突堤周界。
[0030]
优选地，所述步骤s2中的schwarz-christoffel保角变换具体为：采用schwarz-christoffel保角变换公式，将z平面的物理域保角变换到w2上半平面的数学域，然后应用w2＝ew将w2上半平面映射为宽为π的无限长条。
[0031]
优选地，所述步骤s2中不同非对称式防波堤布置构型包括：
[0032]
第一防波堤布置构型，
[0033]
第二防波堤布置构型，0＜β＜1，βπ≤α＜0；
[0034]
第三防波堤布置构型，β＝1，0≤α＜2π。
[0035]
优选地，所述第一防波堤布置构型对应的波浪绕射系数模型为：
[0036][0037][0038][0039]
外域波高：
[0040]
ξ＝a1e
βu
ꢀꢀ
(12)
[0041][0042][0043][0044][0045]
内域波高：
[0046][0047][0048][0049][0050][0051][0052]
式中，f
′
out
和f
′
inn
分别为长波入射防波堤时，即口门宽度相对与入射波长小于设定值情况下的外域波高和内域波高，f
out
和f
inn
分别为其它情况下的外域波高和内域波高；d为w2坐标系下ad的距离，为一个常数；x、y为笛卡尔坐标系下的坐标，u、v为经过schwarz-christoffel保角变换以及w2＝ew映射过的坐标；ε、cn为中间常数，ξ、a1、a2为引入的中间参数变量；对于εn，当n＝0时，ε0＝2，n≥1时，εn＝1；k为波数，为波长；j
γ
(x)为第一类bessel函数，为第二类hankel函数，γ为阶数；
[0053]
长波入射防波堤情况下，未知系数dn和en由以下连续条件计算得出：
[0054][0055]f′
out
＝f
′
inn
[0056]
否则，未知系数dn和en由以下连续条件计算得出：
[0057][0058]fout
＝f
inn
。
[0060]
优选地，所述第二防波堤布置构型对应的波浪绕射系数模型为：
[0061]
[0062][0063][0064]
外域波高：
[0065][0066][0067][0068][0069][0070]
内域波高：
[0071]
ξ＝a1e
βu
ꢀꢀ
(31)
[0072][0073][0074][0075][0076][0077]
式中，f
′
out
和f
′
inn
分别为长波入射防波堤时，即口门宽度相对与入射波长小于设定值情况下的外域波高和内域波高，f
out
和f
inn
分别为其它情况下的外域波高和内域波高；d为w2坐标系下ad的距离，为一个常数；x、y为笛卡尔坐标系下的坐标，u、v为经过schwarz-christoffel保角变换以及w2＝ew映射过的坐标；ε、为中间常数，ξ、a1、a2为引入的中间参数变量；对于εn，当n＝0时，ε0＝2，n≥1时，εn＝1；k为波数，为波长；j
γ
(x)为第一类bessel函数，为第二类hankel函数，γ为阶数；
[0078]
长波入射防波堤情况下，未知系数dn和en由以下连续条件计算得出：
[0079][0080]f′
out
＝f
′
inn
[0081]
否则，未知系数dn和en由以下连续条件计算得出：
[0082][0083]
l
out
＝f
inn
。
[0085]
优选地，所述第三防波堤布置构型对应的波浪绕射系数模型为：
[0086][0087][0088][0089]
外域波高：
[0090]
ξ＝a1euꢀꢀ
(40)
[0091]
a1＝kε
ꢀꢀ
(41)
[0092][0093][0094][0095]
内域波高：
[0096][0097]
a2＝kεd
ꢀꢀ
(46)
[0098][0099][0100][0101][0102]
式中，f
′
out
和f
′
inn
分别为长波入射防波堤时，即口门宽度相对与入射波长小于设定值情况下的外域波高和内域波高，f
out
和f
inn
分别为其它情况下的外域波高和内域波高；d为w2坐标系下ad的距离，为一个常数；x、y为笛卡尔坐标系下的坐标，u、v为经过schwarz-christoffel保角变换以及w2＝ew映射过的坐标；ε、cn为中间常数，ξ、a1、a2为引入的中间参数变量；对于εn，当n＝0时，ε0＝2，n≥1时，εn＝1；k为波数，为波长；j
γ
(x)为第一类bessel函数，为第二类hankel函数，γ为阶数；
[0103]
长波入射防波堤情况下，未知系数dn和en由以下连续条件计算得出：
[0104][0105]f′
out
＝f
′
inn
[0106]
否则，未知系数dn和en由以下连续条件计算得出：
[0107][0108]fout
＝f
inn
。
[0110]
优选地，所述步骤s3中采用法对波浪绕射系数模型进行数值求解，得到波浪绕射系数解析值，具体为：
[0111]
对波浪绕射系数模型中的表征波高的二重积分方程求解过程具体为：
[0112]
将积分区间[a
′
，b
′
]按步长作m等分，区间[c
′
，d
′
]按步长作n等分，坐标为xi＝a
′
i*q(i＝0，1，
…
，m)，yj＝c
′
j*p(j＝0，1，
…
，n)，则表征波高的积分方程的离散形式为：
[0113][0114]
式中，区间[a
′
，b
′
]代表变量s的范围，[c
′
，d
′
]代表变量t的范围，f(x，y)为未知函数，a(x，y)为已知函数，g(x，y，s，t)为核函数；
[0115]
采用梯形公式对式(51)中的二重积分进行离散：
[0116][0117]
离散后的积分方程转化为一个线性方程组，求解此线性方程组得到积分方程的近似解。
[0118]
优选地，所述方法还包括对积分方程中含有的无穷积分项进行截断处理，即选取一个有限值来近似无穷积分上限。
[0119]
与现有技术相比，本发明具有以下优点：
[0120]
1)本发明提出的一种用于非对称双突堤的波浪绕射解析方法，基于schwarz-christoffel保角变换以及格林函数法对helmholtz方程的边值问题进行求解，应用该方法得到了计算不同防波堤布置构型的绕射系数模型，并采用法进行数值求解，解析得到不同非对称式防波堤布置构型的波浪绕射分布情况，该方法首次考虑了非对称双突堤构型下的波浪绕射问题，填补了非对称防波堤波浪绕射理论的空白，为日后研究不规则波入射非对称构型港域的波浪绕射问题奠下了基础；
[0121]
2)本发明对三种不同的防波堤布置构型建立绕射系数模型，考虑场景更为全面，模型的适用性高；
[0122]
3)本发明针对口门宽度和入射波长之间的比例情况，分别给出对应的求解表达式，尤其考虑了长波入射防波堤时，即口门宽度od相对与入射波长很小的情况下的外域波高和内域波高，可针对实际应用环境选择合适的模型进行波浪绕射系数解析，兼顾了准确性和求解效率。
[0123]
4)本发明通过对积分求解过程中的无穷项进行截断处理，可一定程度提高求解速
率。
附图说明
[0124]
图1为本发明的方法流程图；
[0125]
图2为非对称平面布置的双突堤示意图；
[0126]
图3为物理域至数学域的保角映射；其中，图3a为图1中z平面的物理域保角示意图；图3b为图3a中w2平面上半平面的保角映射示意图；
[0127]
图4为不同入射角时防波堤后波浪绕射系数的比较；
[0128]
图5为布置夹角不同的防波堤后的波浪绕射系数比较；
[0129]
图6为布置夹角不同的防波堤后的波浪绕射系数比较。
具体实施方式
[0130]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明的一部分实施例，而不是全部实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例，都应属于本发明保护的范围。
[0131]
实施例
[0132]
如图1所示，本实施例给出了一种用于非对称双突堤波浪绕射的波高分布预测方法，该方法包括以下步骤：
[0133]
步骤s1、建立笛卡尔坐标系下的非对称式防波堤模型；
[0134]
步骤s2、基于速度势函数及线性化自由面边界条件，得到关于速度势函数中复函数的helmholtz方程；采用schwarz-christoffel保角变换以及格林函数法对helmholtz方程进行边值求解，得到不同非对称式防波堤布置构型的波浪绕射系数模型；
[0135]
步骤s3、采用法对波浪绕射系数模型进行数值求解，得到波浪绕射系数解析值。
[0136]
接下来，对本法实施例的方法进行详细介绍。
[0137]
1、非对称式防波堤
[0138]
如图2所示的非对称式防波堤的平面布置图及相关坐标系，具体为：两个半无限长防波堤布置于笛卡尔坐标系oxyz中，一个防波堤置于x轴，另一个防波堤以β角度倾斜布置，两堤间的口门宽度od为l，即od线段的长度。假设x，y轴位于水平面上，z轴垂直向上，均匀水深hs，防波堤无限薄、直立不透水且完全反射，波浪以沿与x轴正方向夹角为α的方向入射传播。
[0139]
2、数学建模
[0140]
假设流体不可压且无旋，则存在速度势函数并满足laplace方程；
[0141]
线性化自由面边界条件，得到速度势函数φ(x，y，z，t)的边值问题，数学表达式为：
[0142]
[0143][0144][0145][0146]
式中，hs为均匀水深，η为自由表面位移，g为重力加速度，t为时间。
[0147]
其中，速度势函数φ(x，y，z，t)的数学表达式为：
[0148]
φ(x，y，z，t)＝a coshk(z hs)f(x，y)e
iσt
ꢀꢀ
(5)
[0149]
式中，k为波数，为波长；σ为角频率，f(x，y)是复函数，a为；
[0150]
将式(5)代入式(1)，得到关于复函数f(x，y)的helmholtz方程：
[0151][0152]
将式(5)代入式(3)-(4)得到频散关系式：
[0153]
σ2＝qktanh(khs)
ꢀꢀ
(7)
[0154]
绕流边界条件为：
[0155][0156]
式中，为法向量，γ为在水面处的突堤周界，对应于图2中oxy面上的bd线段和bc线段以及在无穷远处的辐射条件。
[0157]
为了求解式(6)的边值问题，采用schwarz-christoffel保角变换公式，将图2所示(z平面)的物理域保角变换到如图3a所示(w2平面)的上半平面的数学域。然后应用w2＝ew将图3a所示的w2上半平面映射为图3b所示的宽为π的无限长条。
[0158]
其中，schwarz-christoffel保角变换公式为：
[0159][0160]
下表1为保角变换时图2与图3各点之间的对应关系。
[0161]
表1
[0162][0163][0164]
3、计算不同防波堤布置构型的绕射系数的数学模型
[0165]
1)第一种情况：
[0166][0167]
[0168][0169]
ξ＝a1e
βu
ꢀꢀ
(13)
[0170][0171][0172][0173][0174][0175][0176][0177][0178][0179][0180]
2)第二种情况：0＜β＜1，βπ≤α＜0
[0181][0182][0183][0184][0185][0186]
3)第三种情况：β＝1，0≤α＜2π
[0187]
[0188][0189][0190]
ξ＝a1euꢀꢀ
(32)
[0191]
a1＝kε
ꢀꢀ
(33)
[0192][0193][0194][0195][0196]
a2＝kεd
ꢀꢀ
(38)
[0197][0198][0199][0200][0201]
式中，f
′
out
和f
′
inn
分别为长波入射防波堤时，即口门宽度相对与入射波长小于设定值情况下的外域波高和内域波高，f
out
和f
inn
分别为其它情况下的外域波高和内域波高；d为w2坐标系下ad的距离，为一个常数；x、y为笛卡尔坐标系下的坐标，u、v为经过schwarz-christoffel保角变换以及w2＝ew映射过的坐标；ε、cn、为中间常数，ξ、a1、a2为引入的中间参数变量；对于εn，当n＝0时，ε0＝2，n≥1时，εn＝1；k为波数，为波长；j
γ
(x)为第一类bessel函数，为第二类hankel函数，γ为阶数；
[0202]
长波入射防波堤情况下，未知系数dn和en由以下连续条件计算得出：
[0203][0204]f′
out
＝f
′
inn
[0205]
否则，未知系数dn和en由以下连续条件计算得出：
[0206][0207]fout
＝f
inn
。
[0209]
4、采用法对模型进行数值求解
[0210]
将区间[a
′
，b
′
]按步长作m等分，区间[c
′
，d
′
]按步长作n等分，坐标为xi＝a
′
i*q(i＝0，1，
…
，m)，yj＝c
′
j*p(j＝0，1，
…
，n)，则积分方程(17)、(22)、(25)、(27)、(36)和(41)的离散形式为：
[0211][0212]
采用梯形公式对式(43)中的二重积分进行离散：
[0213][0214]
离散后的积分方程转化为一个线性方程组，求解此线性方程组则可得到积分方程的近似解。在应用式(44)时，由于模型中的积分方程中含有无穷积分，需要对无穷积分项进行截断处理，即选取一个有限值来近似无穷积分上限，该有限值的选取需要具体问题具体分析。值得注意的是对于无穷级数的处理，若无穷级数取的项数过大，求解积分方程时所得到的系数矩阵的条件数过大，系数矩阵奇异，从而导致求得的解错误。
[0215]
本实施例针对不同情况的防波堤布置构型的波浪绕射系数进行了解析计算，对应的结果分别为：
[0216]
1)当防波堤倾斜夹角参数为口门宽度为δ＝1.0时，对不同入射角α防波堤后的波浪绕射系数进行数值求解，具体计算参数见表2，其计算结果如附图4所示。
[0217]
2)当波浪入射角为α＝270
°
，口门宽度为δ＝1.0时，对布置夹角不同的防波堤后的波浪绕射系数进行求解，具体计算参数见表3，其计算结果如附图5所示。
[0218]
3)波浪入射角为α＝90
°
，口门宽度为δ＝1.0时，对布置夹角不同的防波堤后的波浪绕射系数进行求解，具体计算参数见表4，计算结果如附图6所示。
[0219]
注：图中的所有长度均以波长λ无量纲化，即
[0220]
表2
[0221][0222]
表3
[0223]
[0224]
表4
[0225][0226]
以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到各种等效的修改或替换，这些修改或替换都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应以权利要求的保护范围为准。