一种广义模迭代法应用于混合尺寸单元电路合法化方法

1.本发明涉及超大规模集成电路物理设计自动化领域，具体涉及一种广义模迭代法应用于混合尺寸单元电路合法化方法。


背景技术：

2.超大规模集成电路设计流程包括架构设计、功能和逻辑设计、电路设计、物理设计、物理验证和后仿真、制造、封装和测试等过程，其中物理设计直接会影响电路性能、面积、可靠性、功率和制造产量，由于物理设计具有高复杂度，因此会分解成几个关键步骤，布局则是其中一个步骤，布局是确定每个单元在相应模块中的位置的一个过程，布局问题是np-难问题；然而芯片中的单元通常数量巨大，因此问题规模也相当庞大，精确求解变得相当困难，通常采用一些近似方法来求解，获得近似最优解，而如何快速有效地逼近最优解是当前亟待解决的问题。
3.布局阶段通常分为三个阶段：全局布局、合法化、详细布局；其中合法化力求将单元布置到行列中去，并消除单元间重叠，同时以最小化全局布局中的位移为目标。
4.门电路设计复杂度的增加，导致标准单元通常被设计成不同尺寸。混合尺寸单元的布局则带来了前所未有的挑战；现有的合法化算法主要有网络流算法、启发式算法、解析式算法；现有算法通常是针对单元进行逐个处理，无法从全局的角度出发。陈建利等(cn106971042a)提出了将合法化问题中二次规划问题转化成线性互补问题，并应用模系矩阵分裂迭代法对该问题进行求解，该方法从一种全局的角度考虑合法化问题。为了进一步提高该方法的收敛速度，本发明提出了一种广义的模系矩阵分裂迭代法，通过选取适当的参数矩阵，可推导出现有的模系矩阵分裂迭代法的合法化算法。


技术实现要素：

5.发明目的：本发明的目的是为了解决现有技术中的不足，提供一种广义模系矩阵分裂迭代法应用于混合尺寸单元电路合法化，首先对多倍行高单元进行预处理，接着将合法化问题建立成二次规划模型，然后利用kkt条件将二次规划问题转换成线性互补问题，并利用广义的模系矩阵分裂迭代法求解，最后将多倍行高标准单元进行复原。与现有技术相比，本发明通过选取合适的参数矩阵ω1，ω2，加快了迭代过程的收敛速度，并提供了一种求解混合尺寸标准单元电路合法化问题的模系矩阵分裂法的一个通用框架。
6.为了实现以上目的，本发明提供一种广义模迭代法应用于混合尺寸单元电路合法化方法，包括如下步骤：
7.s1:将多倍行高标准单元进行预处理；
8.s2:将标准单元从固定宏块中移除；
9.s3:将混合尺寸标准单元合法化问题描述成二次规划的数学模型；
10.s4:将二次规划模型转换成线性互补问题；
11.s5:用广义的模系矩阵分裂迭代法求解线性互补问题；
12.s6:将多倍行高标准单元进行还原。
13.进一步的，所述步骤s1的具体实现方式包括：芯片的布局区域用其左下角坐标(0,0)和右上角坐标(w,h)表示，w表示布局区域的宽度，h表示布局区域的高度，待布局的标准单元集为c＝(c1,c2,
…cn
)，其中单元ci的初始左下角坐标为宽度及高度分别为wi，hi，合法化之后的坐标为(xi,yi)，对于多倍行高标准单元，将其表示成多个子单元，用(c
i1
,c
i2
,
…cit
)表示，其中，t表示标准单元的高度与行高的比值。
14.进一步的，所述步骤s2中，由于标准单元中可能存在面积较大的宏块，对于这类单元，通常将其位置固定，不会随意移动它们，因此在布局中，这类宏块变成了障碍物，在该步骤中，将与宏块重叠的可移动标准单元从其上移出，移到最近的不与宏块重叠的位置上去。
15.进一步的，所述步骤s3中，假设标准单元已经对齐到最近的与其电源类型相匹配的行上，合法化过程是以标准单元总位移最小为目标，并消除单元之间的重叠，可描述为如下述模型(1):
[0016][0017]
上述模型为凸二次规划问题，可写为标准形式：
[0018][0019]
其中，b是一个单位矩阵，为一个列向量，由于单元之间不能相互重叠，因此任意相邻的单元间应满足x
j-xi≥wi(xj≥xi)，若任意两个相邻的单元对都满足该条件，则可以写成wx≥d，矩阵w为相邻单元间的约束矩阵，它的每一行仅包含2个元素，即-1和1，分别表示每一个相邻单元对中的左侧和右侧的单元，向量d中对应的分量表示左侧单元的宽度，若该左侧单元紧邻宏块，其宽度为单元本身的宽度加上宏块的宽度；则矩阵w和向量d的行数为约束的个数，w为多倍行高单元的约束矩阵，它的列数为经预处理后总的标准单元数，即单倍行高单元的数量加上多倍行高单元分成的所有子单元数量，矩阵r中每一行同样由2个元素，即-1和1组成，分别表示同一个多倍行高单元相邻两行的子单元，约束rx＝0了保证其子单元x坐标相等；
[0020]
应用拉格朗日乘子法，将二次规划中的等式约束加入到目标函数中，则(8)可表示为：
[0021][0022]
其中，λ为拉格朗日乘子。
[0023]
进一步的，所述步骤s4中，根据karush-kuhn-tucker(kkt)条件，可知存在向量r,u，使得(x,r,u)满足如下kkt条件：
[0024][0025]
在方程组(5)中的不等式约束d-wx≤0加入松弛系数e且e》0，使得d-wx e＝0，则wx-d＝e,将方程组(8)改下为如下形式：
[0026][0027]
将方程组(5)改下为如下形式：
[0028][0029]
令该问题则是找到一对解向量满足如下条件：
[0030]
w＝az q≥0,z≥0 and w
t
z≥0.
ꢀꢀ
(7)
[0031]
问题(8)则为线性互补问题。
[0032]
进一步的，所述步骤s5的具体实施方式为：令z＝ω1(|v| v)，w＝ω2(|v|-v)，为aω1的一个分裂，则(8)可等价地转换成如下绝对值方程：
[0033][0034]
给定一个任意的初始向量求解线性系统来计算v
k 1
的值，直到迭代序列收敛，
[0035][0036]
且
[0037]z(k 1)
＝ω1(|v
(k 1)
| v
(k 1)
)，k＝0,1,2,
…
[0038]
特别地，若ω2＝ω，则该方法可推导出现有的模系矩阵分裂迭代法；本发明中，取ω1＝ωi，ω2＝tda，da为矩阵a的分块三对角矩阵；选取的如下所示：
[0039][0040]
其中，β，θ为正常数，f＝tridiag(w(b λr
t
r)-1wt
)是矩阵a的舒尔补矩阵w(b λr
t
r)-1wt
的三对角矩阵；鉴于矩阵求逆计算的时间复杂度，可应用sherman-morrison公式进行简化；因为rr
t
是对角线元素均为2的对角矩阵，且矩阵b又是一个单位矩阵，那么(b λr
t
r)-1
可用
如下等式表示：
[0041][0042]
因此，
[0043]
进一步的，述步骤s6中，将每个多倍行高标准单元的所有子单元按照x坐标按照升序排序，则中位数为求得的该多倍行高单元的x坐标。
[0044]
本发明的上述技术方案相比现有技术具有以下优点：(1)将合法化的二次规划模型转换成线性互补问题，采用了高效的模方法进行求解。(2)通过选取合适的参数矩阵ω1，ω2和正常数ω，β，θ，可以进一步加快迭代过程的收敛速度，在更短的时间内可得到最优解或近似最优解；(3)特别地，若取ω2＝ω，可推导出现有的基于模系矩阵分裂迭代法的合法化算法，提供了一种求解混合尺寸标准单元电路合法化问题的模系矩阵分裂法的一个通用框架。(4)针对合法化问题中涉及的鞍点型矩阵求解，提供了一种新的求解方法。
附图说明
[0045]
下面结合附图，通过对本发明的具体实施方式详细描述，将使本发明的技术方案及其有益效果显而易见。
[0046]
图1是混合尺寸标准单元电路合法化过程的流程图；
[0047]
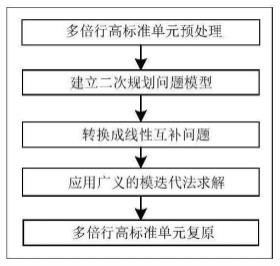
图2是广义模系矩阵分裂迭代法求解步骤图。
具体实施方式
[0048]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅是本发明一部分实施例，而不是全部的实施例，基于本发明中的实施例，本领域技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0049]
如图1-2所示，一种广义模迭代法应用于混合尺寸单元电路合法化方法，包括如下步骤：
[0050]
s1:将多倍行高标准单元进行预处理；
[0051]
s2:将标准单元从固定宏块中移除；
[0052]
s3:将混合尺寸标准单元合法化问题描述成二次规划的数学模型；
[0053]
s4:将二次规划模型转换成线性互补问题；
[0054]
s5:用广义的模系矩阵分裂迭代法求解线性互补问题；
[0055]
s6:将多倍行高标准单元进行还原。
[0056]
本实例中进一步的，所述步骤s1的具体实现方式包括：芯片的布局区域用其左下角坐标(0,0)和右上角坐标(w,h)表示，w表示布局区域的宽度，h表示布局区域的高度，待布局的标准单元集为c＝(c1,c2,
…cn
)，其中单元ci的初始左下角坐标为宽度及高度分别为wi，hi，合法化之后的坐标为(xi,yi)，对于多倍行高标准单元，将其表示成多个子单元，用(c
i1
,c
i2
,
…cit
)表示，其中，t表示标准单元的高度与行高的比值。
[0057]
本实例中进一步的，所述步骤s2中，由于标准单元中可能存在面积较大的宏块，对于这类单元，通常将其位置固定，不会随意移动它们，因此在布局中，这类宏块变成了障碍物，在该步骤中，将与宏块重叠的可移动标准单元从其上移出，移到最近的不与宏块重叠的位置上去。
[0058]
本实例中进一步的，所述步骤s3中，假设标准单元已经对齐到最近的与其电源类型相匹配的行上，合法化过程是以标准单元总位移最小为目标，并消除单元之间的重叠，可描述为如下述模型(1):
[0059][0060]
上述模型为凸二次规划问题，可写为标准形式：
[0061][0062]
其中，b是一个单位矩阵，为一个列向量，由于单元之间不能相互重叠，因此任意相邻的单元间应满足x
j-xi≥wi(xj≥xi)，若任意两个相邻的单元对都满足该条件，则可以写成wx≥d，矩阵w为相邻单元间的约束矩阵，它的每一行仅包含2个元素，即-1和1，分别表示每一个相邻单元对中的左侧和右侧的单元，向量d中对应的分量表示左侧单元的宽度，若该左侧单元紧邻宏块，其宽度为单元本身的宽度加上宏块的宽度；则矩阵w和向量d的行数为约束的个数，w为多倍行高单元的约束矩阵，它的列数为经预处理后总的标准单元数，即单倍行高单元的数量加上多倍行高单元分成的所有子单元数量，矩阵r中每一行同样由2个元素，即-1和1组成，分别表示同一个多倍行高单元相邻两行的子单元，约束rx＝0了保证其子单元x坐标相等；
[0063]
应用拉格朗日乘子法，将二次规划中的等式约束加入到目标函数中，则(8)可表示为：
[0064][0065]
其中，λ为拉格朗日乘子。
[0066]
本实例中进一步的，所述步骤s4中，根据karush-kuhn-tucker(kkt)条件，可知存在向量r,u，使得(x,r,u)满足如下kkt条件：
[0067][0068]
在方程组(5)中的不等式约束d-wx≤0加入松弛系数e且e》0，使得d-wx e＝0，则
wx-d＝e,将方程组(8)改下为如下形式：
[0069][0070]
将方程组(8)改下为如下形式：
[0071][0072]
令该问题则是找到一对解向量满足如下条件：
[0073]
w＝az q≥0,z≥0 and w
t
z≥0.
ꢀꢀ
(7)
[0074]
问题(8)则为线性互补问题。
[0075]
本实例中进一步的，所述步骤s5的具体实施方式为：令z＝ω1(|v| v)，w＝ω2(|v|-v)，为aω1的一个分裂，则(8)可等价地转换成如下绝对值方程：
[0076][0077]
给定一个任意的初始向量求解线性系统来计算v
k 1
的值，直到迭代序列收敛，
[0078][0079]
且
[0080]z(k 1)
＝ω1(|v
(k 1)
| v
(k 1)
)，k＝0,1,2,
…
[0081]
特别地，若ω2＝ω，则该方法可推导出现有的模系矩阵分裂迭代法；本发明中，取ω1＝ωi，ω2＝tda，da为矩阵a的分块三对角矩阵；选取的如下所示：
[0082][0083]
其中，β，θ为正常数，f＝tridiag(w(b λr
t
r)-1wt
)是矩阵a的舒尔补矩阵w(b λr
t
r)-1wt
的三对角矩阵；鉴于矩阵求逆计算的时间复杂度，可应用sherman-morrison公式进行简化；因为rr
t
是对角线元素均为2的对角矩阵，且矩阵b又是一个单位矩阵，那么(b λr
t
r)-1
可用如下等式表示：
[0084][0085]
因此，
[0086]
本实例中进一步的，所述步骤s6中，将每个多倍行高标准单元的所有子单元按照x
坐标按照升序排序，则中位数为求得的该多倍行高单元的x坐标。
[0087]
以上所述仅为本发明的示例性实施例，并非因此限制本发明专利保护范围，凡是利用本发明说明书及附图内容所作的等效结构或等效流程变换，或直接或间接运用在其他相关的技术领域，均同理包括在本发明的专利保护范围内。